2017.08.15【NOIP提高组】模拟赛B组

Summary

　　今天比赛很差很差，掉到谷底。第一题快排打错了，漏了递归，变成一个while循环。最后一题k忘记减一，答案一直是无穷大，所以没交。第三题没时间调DP就打了个递归，第二题状态想歪了。四道题有三道DP的，一道小码力的。DP可见很差，还要多学，多做。快排打到一半傻乎乎就没打了，样例数据又刚好都是对的，不会对拍。马上就要学一下啊！

Problem

T1 平台

题目大意

　　给你一堆平台，每个平台平行于x轴，距离x轴有个高度h。每个平台由两个柱子支撑，分别在离端点0.5个单位的位置。问柱子的长度和

想法

　　鉴于平台个数很小，平台的横坐标小，直接暴力即可。

　　先将平台高度从小到大排序，然后用bz数组，bz[i]表示横坐标为i时，上面最高的平台高度是多少，每次查找就行了。

　　因为有0.5这种小数的情况，所以可以将所有坐标乘以二。

T2 单足跳

题目大意

　　游戏在一行N个方块中进行，编号为1到N，一开始Alice在方块1中，第一次只能跳到方块2中，接下来每一次跳跃必须满足以下两个限制：
　　（1） 如果是向前跳（即跳到比现在编号大的方块），跳跃距离必须比上一次要大1；
　　（2） 如果是向后跳（即跳到比现在编号小的方块），跳跃距离必须跟上一次一样。

　　每个方块有个花费值，问从方块1到方块n的最小花费值。

想法

　　考试的时候我是这么设的

　　f[i,j]表示第i次到j这个位置的最小花费值，怎么转移都不对。大家也可以想一下，评论一下。

　　正解是这样的

　　设f[i,j]表示你花费i步走到j这个位置。

　　显然，我们两种方案，一种往前，一种往后

　　往前的情况：

　　我们会到达j-i这个位置，根据题目意思，同样是花费i步过去，所以这么转移f[i,j-i]=min{f[i,j-i],f[i,j]+a[j-i]}

　　当然，j一定符合范围

　　往后的情况：

　　我们会往后跳i+1位，即到达j+i+1这个位置，他是花费i+1步过去，故转移为f[i+1,j+i+1]=min{f[i+1,j+i+1,f[i,j]+a[j+i+1]}

　　题目很快就解决完毕了。

T3 生日聚餐

题目大意

　　晚餐由N种原料做成，每道菜所需每种原料的数量是一样的。
　　厨房里有一些原料，但不够，Alice还需要从旁边的超市中购买一些回来。超市里什么原料都有，每种原料都分大包装和小包装。Alice有M元钱，她想利用这M元钱购买原料使得能做出最多的菜。

想法

　　跟之前做过的一道题差不多，同样可以先求完全背包，然后枚举答案，二分答案也是可以的。　　

　　我们用f[i,j]表示第i种材料，用了j数量的最小价值

　　我们求完后需要维护一下f数组，因为可能刚好不能组成j数量的物品，但是用多点钱还是可以买到。例如你5块钱可以买到6块橡皮擦，但是你只需要5块，商店又不能分开买，你买5块橡皮擦，同样也是需要5块钱。

　　然后我们枚举（二分）答案，也就是做多少钱数，我们设这个数为i。

　　答案就是

　　

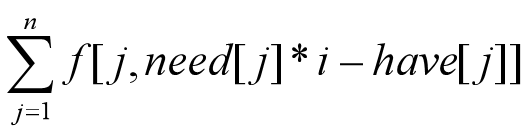
　　显然这个是递增的，取个最大符合条件的值，对应的i就是答案

　   这就是二分求解的东西，故可以用二分

　　f数组的空间会炸，所以可以使用动态数组（可以在程序中根据需要定义数组大小）

　　下面是一维的定义方式（pascal），二维的只需要加多括号内容

　　var

　　　　a:array of (array of) longint;

　　begin

　　　　setlength(a,s,(s1))表示第一维下标开0~s-1大小，括号中，第二维表示下标开从0~s1-1大小

　　end.

T4 数学题

题目大意

　　给你一串数，让他们可以往里面加加号，使之等于一个数，问最少的加加号个数。

想法

　　我们可以想到动态规划。

　　设f[i,j]表示选到前i个数，和为j所加的最少加号个数是多少。

　　我们枚举i,j,k，如图标明位置

　　

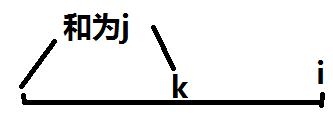
　　其中，我们要把k~i这些数弄成一个数，独立起来，也就是说，在k前面放一个加号。

　　显然，转移就是f[i,j+ans]=min{f[i,j+ans],f[k,j]}，Ans就是k~i这些数组合成一个的那个新的数。

　　还有一种情况就不放加号

　　f[i,j*10+a[i]]=min{f[i,j*10+a[i]],f[i-1,j])。很显然，你这么做最多加4次，你就会被挂了，因为一直不放加号，数的大小可想而知。

　　到目前为止，时间复杂度是O(n³），显然你会炸的巴拉巴拉的

　　唯一可能优化的就是k，其实k枚举这么多是不必要的，关键还是0的问题

　　所以，我们对输入的字符串处理一下，最多只能有4个连续的0

　　时间复杂度：O(4n²)