机器学习基石笔记：12 Nonlinear Transformation

一、二次假设

实际上线性假设的模型复杂度是受到限制的，

需要高次假设打破这个限制。

假设数据不是线性可分的，但是可以被一个圆心在原点的圆分开，

需要我们重新设计基于该圆的PLA等算法吗？

不用，

只需要通过非线性转换将X域圆形可分变为Z域线性可分！

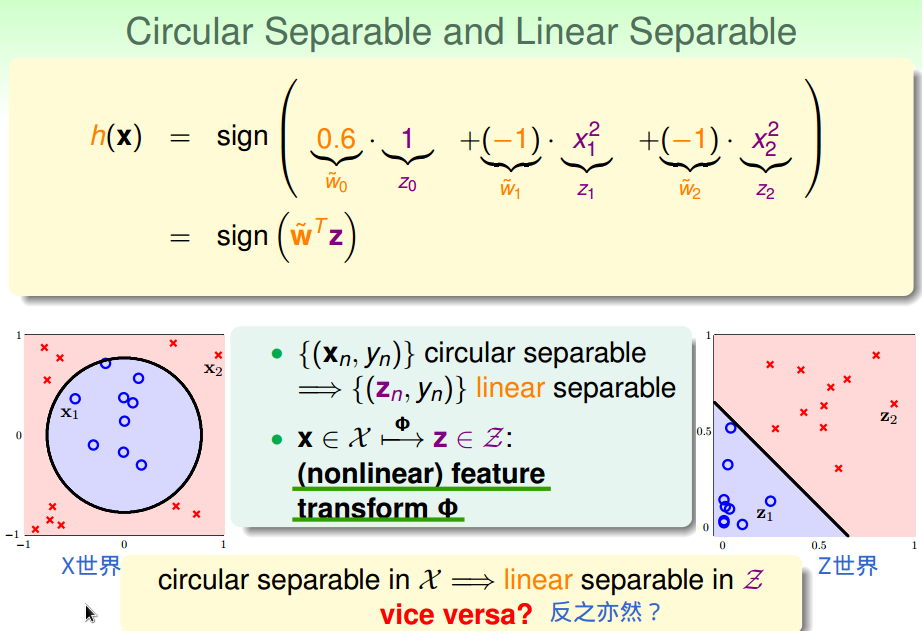
通用的二次假设集：

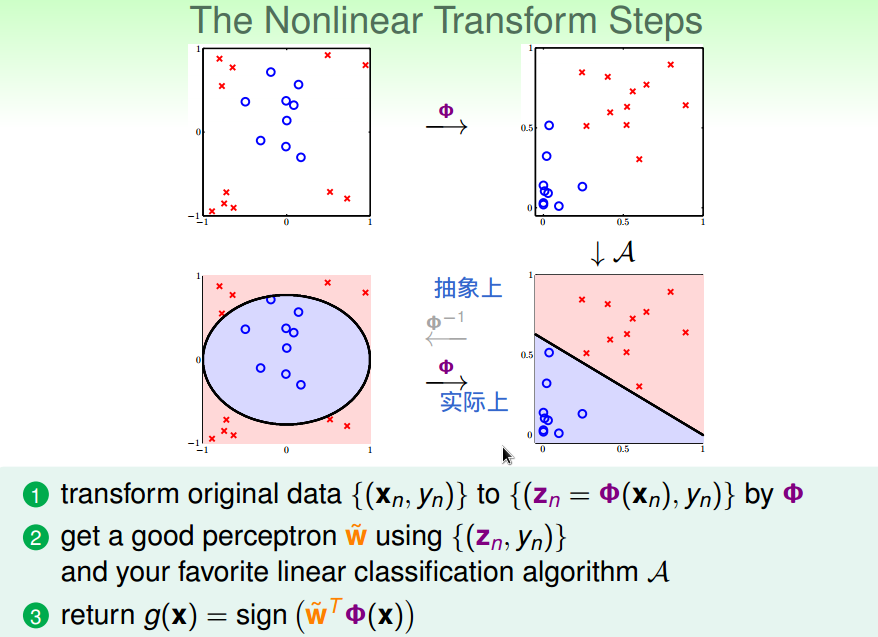
二、非线性转换

好的二次假设：

非线性转换的步骤：

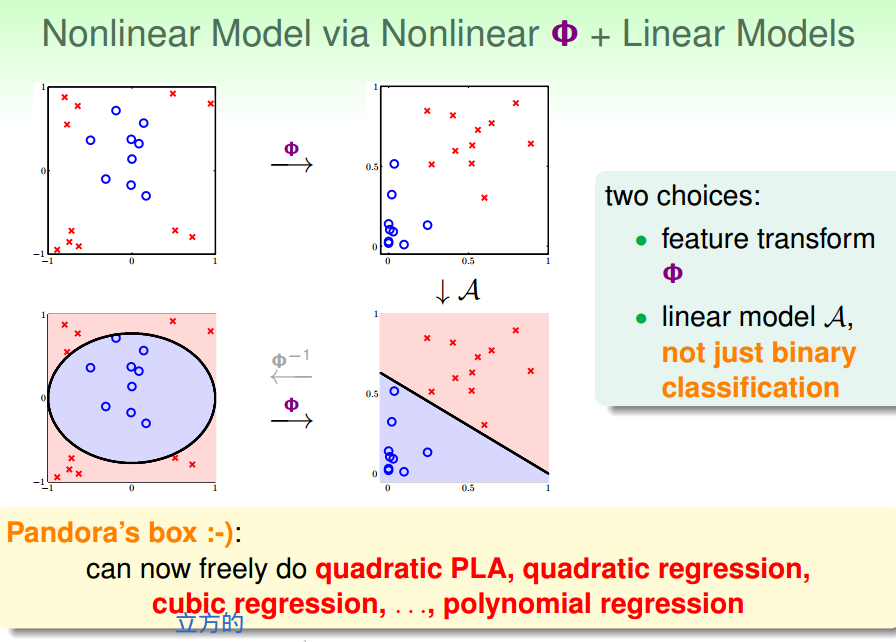
三、非线性转换的代价

计算/存储代价：

次数越高，代价越大。

模型复杂度代价：

次数越高，代价越大。

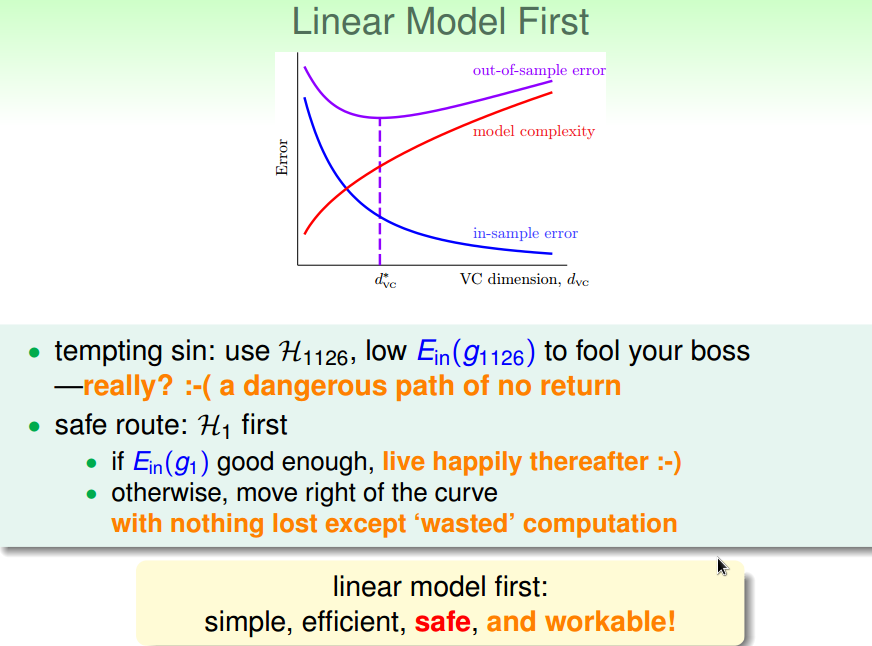
高次假设能使样本内代价更小；

低次假设能保证泛化误差更小。

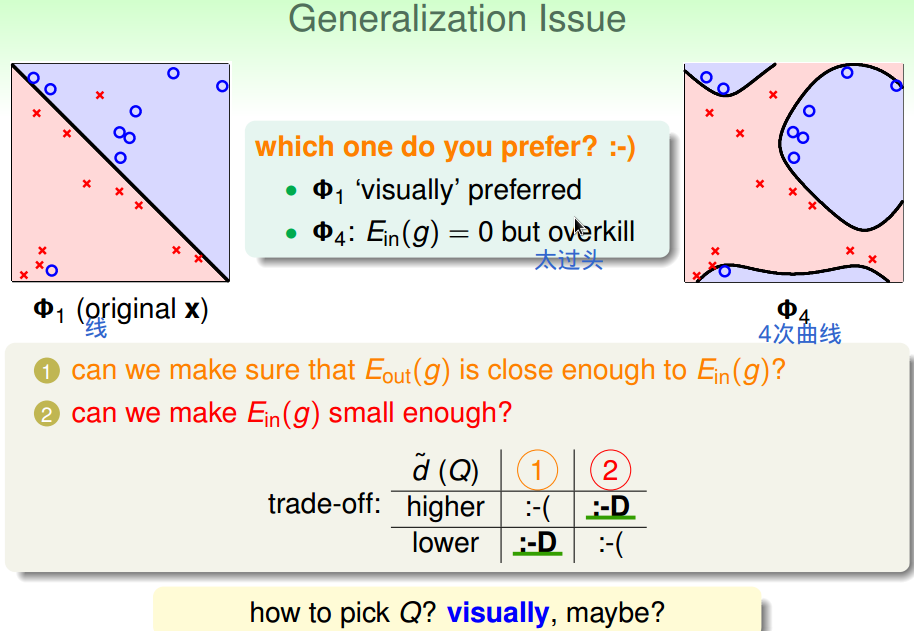
可视化数据后再选择：

一是数据维度高时难以可视化；

二是可视化后再选择实际上人脑里产生的模型复杂度代价并没有算进去，

加上后实际代价不一定很低。

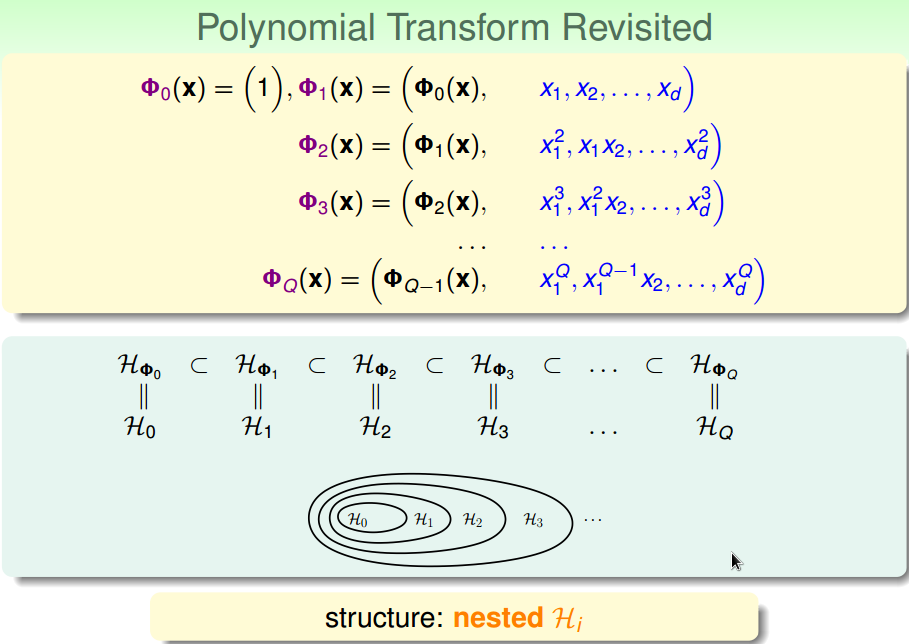
四、结构化假设集

低价假设集合是包含在高次假设集合中的。

先线性模型，效果不好的话，再使用更高次点的模型。