arctan

ArcTan
When the ArcTan functional configuration is selected, the input vector (X_IN,Y_IN) is rotated
(using the CORDIC algorithm) until the Y component is zero. This generates the output
angle, Atan(Y_IN/X_IN).
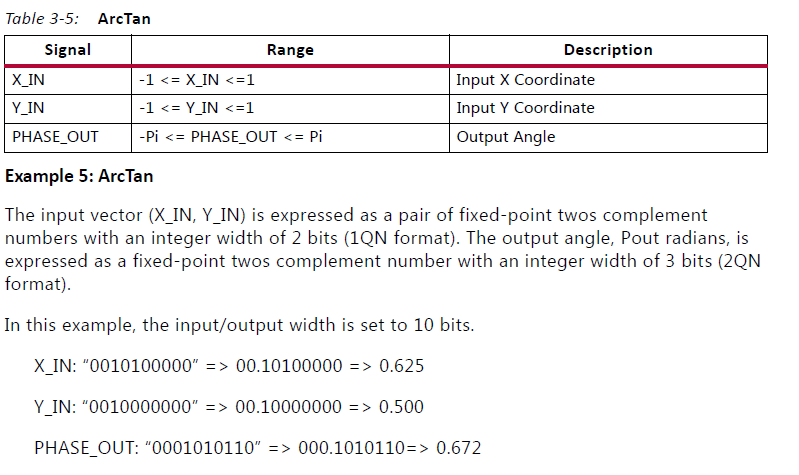
The inputs, X_IN and Y_IN, are limited to the ranges given in Table 3-5 when coarse rotation
is set. Inputs outside these ranges produce unpredictable outputs. See Input/Output Data
Representation for more information about CORDIC binary data formats.
An optional coarse rotation module is provided to extend the range of inputs X_IN and Y_IN
to the full circle. For this functional configuration, the coarse rotation module is selected by
default, but can be manually deselected. See Advanced Configuration Parameters for more
information. When this option is not set, inputs must be constrained to lie in the first
quadrant, -Pi/4 to + Pi/4.
The compensation scaling module is disabled for the ArcTan functional configuration as no
magnitude data is output. The ArcTan of a zero length vector, (0,0), is indeterminate and the
output angle generated by the core is undefined.
The accuracy of the output angle from the CORDIC vector translation algorithm is limited by
the number of significant magnitude bits of the input vector (X_IN, Y_IN). See Output
Quantization Error for more information.