机器人关节空间轨迹规划--S型速度规划

• 关节空间 VS 操作空间

　　关节空间与操作空间轨迹规划流程图如下（上标$i$和$f$分别代表起始位置initial和目标位置final）：

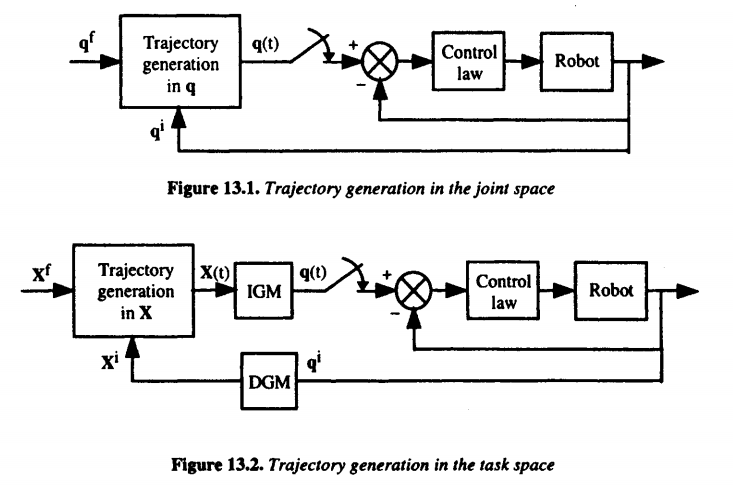
　　在关节空间内进行轨迹规划有如下优点：

1. 在线运算量更小，即无需进行机器人的逆解或正解解算
2. 不受机器人奇异构型影响
3. 可以根据机器人或驱动器手册直接确定最大速度或力矩

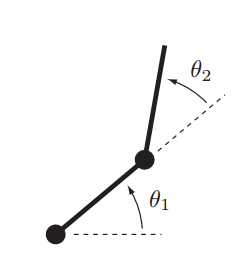
其缺点是对应操作空间的轨迹无法预测，增加了机械臂与环境碰撞的可能。例如，考虑下面的二连杆机构，关节运动的限制为：$0^{\circ} \le \theta_1 \le 180^{\circ}$，$0^{\circ} \le \theta_2 \le 150^{\circ}$

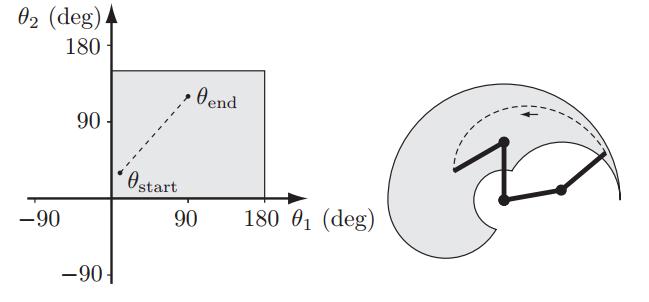
　　下图中，左侧为关节空间内规划的线性运动轨迹，而其对应在操作空间的轨迹却是弧线。机构末端的可达空间在图中由灰色背景表示，其大小和形状受关节运动范围的影响。

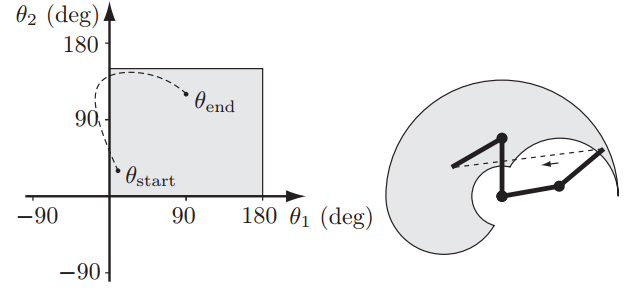
　　下图在操作空间中规划了一条直线轨迹，其对应的关节空间轨迹为一弧线，且在运动过程中超出了关节值限制。操作空间内进行轨迹规划优点是直观，缺点是计算量大（需要计算逆解），会遇到奇异性问题以及关节运动超限等。

　　到底是选择在关节空间还是操作空间内进行轨迹规划，取决于任务需要。需要考虑避障或必须沿特定轨迹运动时选择操作空间轨迹规划，只需考虑速度、力矩、关节范围等运动约束时选择关节空间轨迹规划（The joint space scheme is appropriate to achieve fast motions in a free space）。

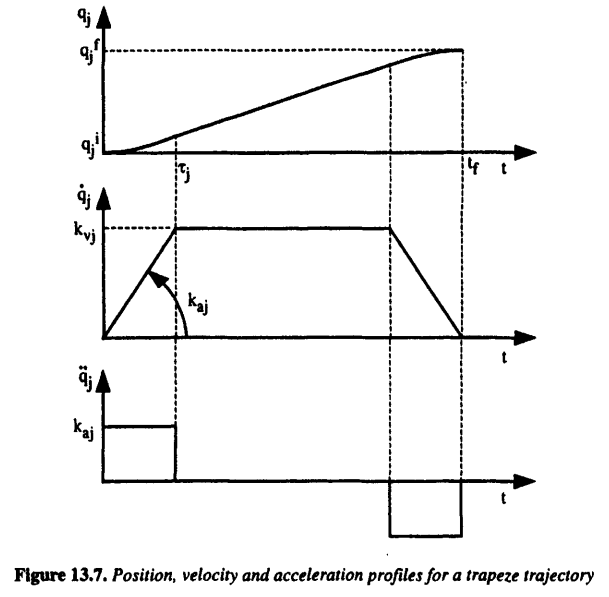
• 梯形速度曲线

　　运动控制系统中常用的梯形速度曲线如下图所示，会出现加速度不连续的情形（从$k_{aj}$到0的跳变），这样可能会导致机械系统出现冲击或不可预料的振动，不过由于机械系统存在一定的弹性并不是绝对刚体，这种加速度不连续造成的冲击会被机械机构滤除或减轻。而对于高速重载的机器人来说，这种加速度不连续造成的影响就不能忽略了。可以参考知乎上这个问题：多轴插补为什么普遍使用梯形速度曲线？

•  S型速度曲线
  

　　为了使加速度连续，可对梯形速度规划中的加速度曲线进行修改，使加速度曲线变为连续的二次曲线(a)或者梯形曲线(b)，如下图所示。其中，$\tau'$为加速段时间，$\lambda_jk_{vj}$为第$j$个关节的最大运动速度

　　下面考虑a方法（Linear Trajectory with Polynomial Blends），关节$j$的运动边界条件如下，即关节$j$初始时刻位置为$q_j^i$，初始速度加速度为0，$\tau'$时刻加速到最大速度$\lambda_ik_{vj}sign(D_i)$，$k_{vj}$为理论上关节$j$允许的最大速度，$\lambda_j$为一比例系数（$0 \le \lambda_j \le 1$），$D_j$为从起始位置到目标位置的位移，它是一个有正负的数值。

　　根据边界条件加速度二次曲线表达式为：$k(t-\tau')t$，对其进行积分，可得$\dot{q_j}(t)=\frac{1}{6}k(2t-3\tau')t^2+C$，根据速度边界条件可知$C=0$，$k=\frac{-6}{\tau'^3}\lambda_jk_{vj}$。于是推算出加速度、速度、位置的表达式分别为：$$\begin{cases}& q_j(t)=q_j^i-\frac{1}{\tau'^3}\lambda_jk_{vj}sign(D_j)(\frac{1}{2}t-\tau')t^3\\&\dot{q_j}(t)=-\frac{1}{\tau'^3}\lambda_jk_{vj}sign(D_j)(2t-3\tau')t^2\\&\ddot{q_j}(t)=-\frac{6}{\tau'^3}\lambda_jk_{vj}sign(D_j)(t-\tau')t  \end{cases}$$

　　加速度在$t=\tau'/2$时最大，其幅值为$\left |\ddot{q}_{jmax} \right |=\frac{3}{2}\frac{\lambda_jk_{vj}}{\tau'}=\upsilon_j k_{aj}$，则有：$$\tau'=\frac{3}{2}\frac{\lambda_jk_{vj}}{\upsilon_j k_{aj}}$$

　　根据上式和$q_j(t)$的表达式，可以计算出加速阶段的位移为：$$|q_j^i-q_j(\tau')|=\frac{3}{4}\frac{(\lambda_jk_{vj})^2}{\upsilon_j k_{aj}}$$

　　速度曲线与时间轴围成的面积为$|D_j|$，根据计算可以得到关系式：$$t'_f=\tau'+\frac{|D_j|}{\lambda_jk_{vj}}$$

　　在加速度为0的阶段（最大速度阶段，$\tau' \le t \le \tau'+h'$），关节速度表达式为：$$q_i(t)=q_j(\tau')+(t-\tau')\lambda_jk_{vj}sign(D_j)$$

　　减速阶段与加速阶段对称($t'_f=2\tau'+h'$)，减速阶段在时间段$\tau'+h' \le t \le t'_f$上的轨迹为：$$\begin{cases}&q_j(t)=q_j^f+\frac{1}{2}[\frac{1}{\tau'^3}(t-3\tau'-h')(t-\tau'-h')^3+(2t-3\tau'-2h')]\lambda_jk_{vj}sign(D_j) \\ &\dot{q_j}(t)=[\frac{1}{\tau'^3}(2t-5\tau'-2h')(t-\tau'-h')^2+1]\lambda_jk_{vj}sign(D_j)  \\  &\ddot{q_j}(t)= \frac{6}{\tau'^3}(t-2\tau'-h')(t-\tau'-h')\lambda_jk_{vj}sign(D_j)\end{cases}$$

　　如果目标点距离初始位置过近，可能达不到最大速度和加速度就要开始减速，考虑以最大速度做匀速直线运动阶段的时间为0这种临界状态（The minimum time $t_f$ is obtained when the parameters $\lambda_j$ and $\upsilon_j$ are the largest），为了能以最大速度运动，位移$|D_j|$必须满足如下条件：$$|D_j| > \frac{3}{2}\frac{k_{vj}^2}{k_{aj}}$$　　如果该条件不能满足，则最大速度值应为：$$k'_{vj}=\sqrt{\frac{2}{3}|D_j|k_{aj}}$$　　前面的计算都只考虑单轴运动的情况，当需要多轴同步时，要考虑运动时间最长的轴（与每个轴的最大速度、运动位移等因素有关），将该时间作为同步运动的时间。在确定了同步时间之后，需要重新计算速度曲线的最大速度（运动快的轴要降低最大速度等待慢的轴），使得各轴在同一时刻到达设定的目标位置。

　　参考《Modeling Identification and Control of Robots》的第 13.3.4节 Continuous acceleration profile with constant velocity phase 以及 libfranka MotionGenerator，修改关节空间轨迹规划代码，并在while循环中进行轨迹生成的模拟。

　　traj.h

#pragma once

#include <array>
#include <Eigen/Core>

struct RobotState
{
    std::array<double, > q_d{};
};

class TrajectoryGenerator
{

public:

    // Creates a new TrajectoryGenerator instance for a target q.
    // @param[in] speed_factor: General speed factor in range [0, 1].
    // @param[in] q_goal: Target joint positions.
    TrajectoryGenerator(double speed_factor, const std::array<double, > q_goal);

    // Calculate joint positions for use inside a control loop.
    bool operator()(const RobotState& robot_state, double time);

private:
    using Vector7d = Eigen::Matrix<double, , , Eigen::ColMajor>;

    using Vector7i = Eigen::Matrix<int, , , Eigen::ColMajor>;

    bool calculateDesiredValues(double t, Vector7d* delta_q_d); // generate joint trajectory 

    void calculateSynchronizedValues();

    static constexpr double DeltaQMotionFinished = 1e-;

    const Vector7d q_goal_;

    Vector7d q_start_;  // initial joint position
    Vector7d delta_q_;  // the delta angle between start and goal

    Vector7d dq_max_sync_;
    Vector7d t_1_sync_;
    Vector7d t_2_sync_;
    Vector7d t_f_sync_;
    Vector7d q_1_;  // q_1_ = q(\tau) - q_start_     

    double time_ = 0.0;

    Vector7d dq_max_ = (Vector7d() << 2.0, 2.0, 2.0, 2.0, 2.5, 2.5, 2.5).finished();   

    Vector7d ddq_max_ = (Vector7d() << , , , , , , ).finished(); 

    Vector7d dq;
};

　　traj.cpp

#include "traj.h"
#include <algorithm>
#include <array>
#include <cmath>

TrajectoryGenerator::TrajectoryGenerator(double speed_factor, const std::array<double, > q_goal)
    : q_goal_(q_goal.data())
{
    dq_max_ *= speed_factor;
    ddq_max_ *= speed_factor;
    dq_max_sync_.setZero();
    q_start_.setZero();
    delta_q_.setZero();
    t_1_sync_.setZero();
    t_2_sync_.setZero();
    t_f_sync_.setZero();
    q_1_.setZero();
}

bool TrajectoryGenerator::calculateDesiredValues(double t, Vector7d* delta_q_d)
{
    Vector7i sign_delta_q;
    sign_delta_q << delta_q_.cwiseSign().cast<int>(); // sign(D_j)
    Vector7d t_d = t_2_sync_ - t_1_sync_;             // h'
    std::array<bool, > joint_motion_finished{};      // motion falgs

    for (size_t i = ; i < ; i++) // calculate joint positions
    {
        if (std::abs(delta_q_[i]) < DeltaQMotionFinished){ // target approaches the goal
            (*delta_q_d)[i] = ;
            joint_motion_finished[i] = true;}
        else {
            if (t < t_1_sync_[i]) {
                (*delta_q_d)[i] = -1.0 / std::pow(t_1_sync_[i], 3.0) * dq_max_sync_[i] * sign_delta_q[i] * (0.5 * t - t_1_sync_[i]) * std::pow(t, 3.0);
                dq[i] = -1.0 / std::pow(t_1_sync_[i], 3.0) * dq_max_sync_[i] * sign_delta_q[i] * (2.0 * t -  * t_1_sync_[i]) * std::pow(t, 2.0);
            }
            else if (t >= t_1_sync_[i] && t < t_2_sync_[i]) {
                (*delta_q_d)[i] = q_1_[i] + (t - t_1_sync_[i]) * dq_max_sync_[i] * sign_delta_q[i];
                dq[i] = dq_max_sync_[i];
            }
            else if (t >= t_2_sync_[i] && t < t_f_sync_[i]) {
                (*delta_q_d)[i] = delta_q_[i] + 0.5 *(1.0 / std::pow(t_1_sync_[i], 3.0) *(t - 3.0 * t_1_sync_[i] - t_d[i]) *std::pow((t - t_1_sync_[i] - t_d[i]), 3.0) + (2.0 * t - 3.0 * t_1_sync_[i] - 2.0 * t_d[i])) *dq_max_sync_[i] * sign_delta_q[i];
                dq[i] = (1.0 / std::pow(t_1_sync_[i], 3.0) *( * t - 5.0 * t_1_sync_[i] -  * t_d[i])*std::pow((t - t_1_sync_[i] - t_d[i]), 2.0) + ) * dq_max_sync_[i] * sign_delta_q[i];
            }
            else {
                (*delta_q_d)[i] = delta_q_[i];    // reach the goal
                joint_motion_finished[i] = true;}
        }
    }

    return std::all_of(joint_motion_finished.cbegin(), joint_motion_finished.cend(),[](bool x) { return x; });
}

void TrajectoryGenerator::calculateSynchronizedValues()
{
    Vector7d dq_max_reach(dq_max_);
    Vector7d t_f = Vector7d::Zero();
    Vector7d t_1 = Vector7d::Zero();
    Vector7i sign_delta_q;
    sign_delta_q << delta_q_.cwiseSign().cast<int>();

    // only consider single axis
    for (size_t i = ; i < ; i++) {
        if (std::abs(delta_q_[i]) > DeltaQMotionFinished) {
            if ( std::abs(delta_q_[i]) < 3.0 / 2.0 * std::pow(dq_max_[i], 2.0) / ddq_max_[i] ) { // the goal not far enough from start position
                dq_max_reach[i] = std::sqrt( 2.0 / 3.0 * delta_q_[i] * sign_delta_q[i] * ddq_max_[i] ); // recalculate the maximum velocity
            }
            t_1[i] = 1.5 * dq_max_reach[i] / ddq_max_[i];
            t_f[i] = t_1[i] + std::abs(delta_q_[i]) / dq_max_reach[i];
        }
    }

    // take account of the slowest axis
    double max_t_f = t_f.maxCoeff();

    // consider the synchronization of multiple axises
    for (size_t i = ; i < ; i++) {
        if (std::abs(delta_q_[i]) > DeltaQMotionFinished) {
            double a = 3.0 / 2.0 * ddq_max_[i];
            double b = -1.0 * max_t_f * std::pow(ddq_max_[i] , 2.0);
            double c = std::abs(delta_q_[i]) * std::pow(ddq_max_[i], 2.0);
            double delta = b * b - 4.0 * a * c;
            if (delta < 0.0) {
                delta = 0.0;
            }
            // according to the area under velocity profile, solve equation "a * Kv^2 + b * Kv + c = 0" for Kv
            dq_max_sync_[i] = (-1.0 * b - std::sqrt(delta)) / (2.0 * a); // Kv: maximum synchronization velocity

            t_1_sync_[i] = 1.5 * dq_max_sync_[i] / ddq_max_[i];
            t_f_sync_[i] =(t_1_sync_)[i] + std::abs(delta_q_[i] / dq_max_sync_[i]);
            t_2_sync_[i] = (t_f_sync_)[i] - t_1_sync_[i];
            q_1_[i] = (dq_max_sync_)[i] * sign_delta_q[i] * (0.5 * (t_1_sync_)[i]);
        }
    }

}

bool TrajectoryGenerator::operator()(const RobotState& robot_state, double time)
{
    time_ = time;

    if (time_ == 0.0)
    {
        q_start_ = Vector7d(robot_state.q_d.data());
        delta_q_ = q_goal_ - q_start_;
        calculateSynchronizedValues();
    }

    Vector7d delta_q_d;
    bool motion_finished = calculateDesiredValues(time_, &delta_q_d);

    std::array<double, > joint_positions;
    Eigen::VectorXd::Map(&joint_positions[], ) = (q_start_ + delta_q_d);

    return motion_finished;
}

　　main.cpp

#define _USE_MATH_DEFINES
#include <math.h>
#include "traj.h"
#include <thread>
#include <iostream>

int main(int argc, char *argv[])
{
    RobotState current_state;
    current_state.q_d = { 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0 };

    double speed_factor = 0.5;
    std::array<double, > q_goal = { M_PI_4, M_PI_2, 0.0 , 0.0 , 0.0 , 0.0, 0.0 };

    TrajectoryGenerator traj_generator(speed_factor, q_goal);

    quint64 count = ;
    bool isfinished = false;
    while (!isfinished)
    {
        isfinished = traj_generator(current_state, count / 1000.0);

        std::this_thread::sleep_for(std::chrono::milliseconds());
        count++;
    }

    std::cout << "Motion finished" << std::endl;

    return ;
}

　　注意以下几点：

　　1. 原examples_common.h代码中的ddq_max_start_为加速度，ddq_max_goal_为减速度（接近目标点，开始减速），大多数情况下两者相等

　　2. 在根据速度曲线与时间轴围成的面积计算最大同步速度的时候，会遇到一元二次方程$a\cdot v_{sync}^2+b\cdot v_{sync}+c=0$求解的问题，对于大于零的两个解要选其中数值小的那个，否则会超过最大速度限制，即取值为$\frac{-b-\sqrt{b^2-4ac}}{2a}$。可以简要证明如下：

　　这两个解分布在$v=\frac{-b}{2a}$的两侧，而$\frac{-b}{2a}=\frac{t_{f}k_a}{3}=\frac{1}{3}(\frac{3}{2}\frac{k_v}{k_a}+\frac{|D_j|}{k_v})k_a=\frac{1}{2}k_v+\frac{1}{2}(\frac{2|D_j|k_a}{3k_v})$，根据$|D_j|$的条件 $\frac{2|D_j|k_a}{3k_v}-k_v=\frac{1}{3k_v}(2|D_j|k_a-3k_v^2)> 0$，因此$\frac{-b}{2a}> k_v$，即值较大的解会超出速度限制。

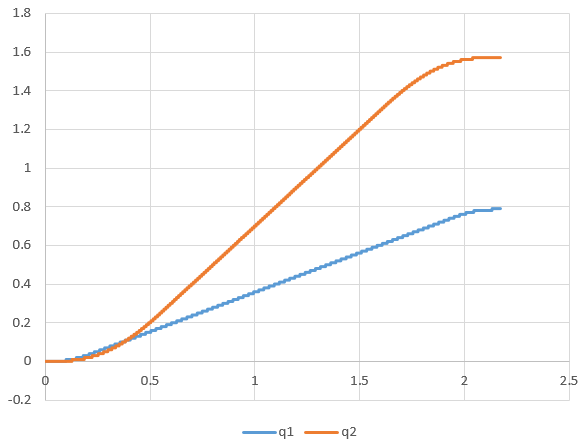
　　将时间、轴1轴2的关节角度和速度保存在CSV文件中，用Excel画出散点图。关节角度随时间变化曲线如下（轴1从0→45°，轴2从0→90°）：

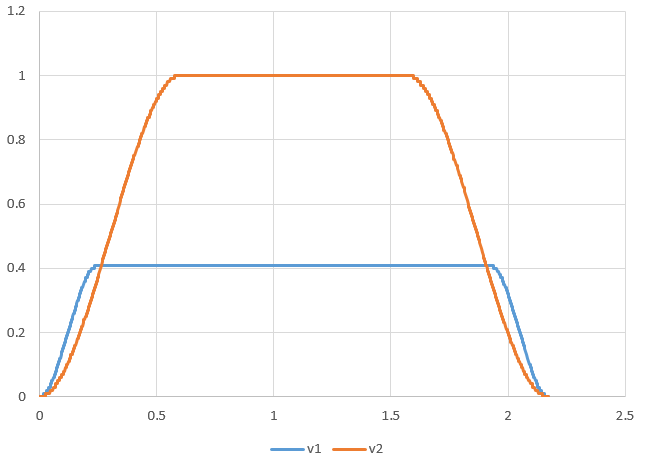
　　关节速度随时间变化曲线如下：

参考：

S型速度规划

线性轨迹的抛物线过渡（梯形加减速）

工业机器人运动轨迹规划方法简述

机器人中的轨迹规划（Trajectory Planning ）

周期同步位置模式(CSP)，轮廓位置模式(PPM)，位置模式(PM)

libfranka MotionGenerator

Robot and interface specifications

Trajectory Planning for Automatic Machines and Robots

Modeling Identification and Control of Robots. 13.3.4 Continuous acceleration profile with constant velocity phase