逻辑回归&线性回归
# coding:utf-8
import numpy as np
from sklearn import linear_model, datasets
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy import fft
from scipy.io import wavfile
n = 40
# hstack数据拼接
# rvs是Random Variates随机变量的意思
# 在模拟X的时候使用了两个正态分布,分别制定各自的均值,方差,生成40个点
X = np.hstack((norm.rvs(loc=2, size=n, scale=2), norm.rvs(loc=8, size=n, scale=3)))
# zeros使得数据点生成40个0,ones使得数据点生成40个1
y = np.hstack((np.zeros(n), np.ones(n)))
# 创建一个 10 * 4 点(point)的图,并设置分辨率为 80
plt.figure(figsize=(10, 4), dpi=80)
# 设置横轴的上下限
plt.xlim((-5, 20))
# scatter散点图
plt.scatter(X, y, c=y)
plt.xlabel("feature value")
plt.ylabel("class")
plt.grid(True, linestyle='-', color='0.75')
plt.savefig("C:/Users/zhen/Desktop/logistic_classify.png", bbox_inches="tight")
# linspace是在-5到15的区间内找10个数
xs = np.linspace(-5, 15, 10)
# ---linear regression----------
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
# reshape重新把array变成了80行1列二维数组,符合机器学习多维线性回归格式
clf.fit(X.reshape(n * 2, 1), y)
def lin_model(clf, X):
return clf.intercept_ + clf.coef_ * X
# --logistic regression--------
from sklearn.linear_model import LogisticRegression
logclf = LogisticRegression()
# reshape重新把array变成了80行1列二维数组,符合机器学习多维线性回归格式
logclf.fit(X.reshape(n * 2, 1), y)
def lr_model(clf, X):
return 1.0 / (1.0 + np.exp(-(clf.intercept_ + clf.coef_ * X)))
# ----plot---------------------------
plt.figure(figsize=(10, 5))
# 创建一个一行两列子图的图像中第一个图
plt.subplot(1, 2, 1)
plt.scatter(X, y, c=y)
plt.plot(X, lin_model(clf, X), "o", color="orange")
plt.plot(xs, lin_model(clf, xs), "-", color="green")
plt.xlabel("feature value")
plt.ylabel("class")
plt.title("linear fit")
plt.grid(True, linestyle='-', color='0.75')
# 创建一个一行两列子图的图像中第二个图
plt.subplot(1, 2, 2)
plt.scatter(X, y, c=y)
plt.plot(X, lr_model(logclf, X).ravel(), "o", color="c")
plt.plot(xs, lr_model(logclf, xs).ravel(), "-", color="green")
plt.xlabel("feature value")
plt.ylabel("class")
plt.title("logistic fit")
plt.grid(True, linestyle='-', color='0.75')
plt.tight_layout(pad=0.4, w_pad=0, h_pad=1.0)
plt.savefig("C:/Users/zhen/Desktop/logistic_classify2.png", bbox_inches="tight")
结果:
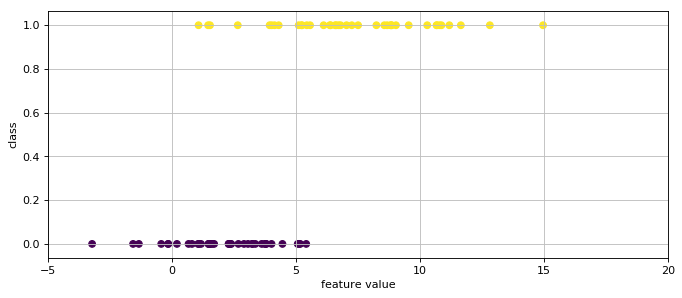

逻辑回归&线性回归的更多相关文章
- 02-12 Logistic(逻辑)回归
目录 逻辑回归 一.逻辑回归学习目标 二.逻辑回归引入 三.逻辑回归详解 3.1 线性回归与逻辑回归 3.2 二元逻辑回归的假设函数 3.2.1 让步比 3.2.2 Sigmoid函数图像 3.3 二 ...
- Matlab实现线性回归和逻辑回归: Linear Regression & Logistic Regression
原文:http://blog.csdn.net/abcjennifer/article/details/7732417 本文为Maching Learning 栏目补充内容,为上几章中所提到单参数线性 ...
- Machine Learning 学习笔记 (1) —— 线性回归与逻辑回归
本系列文章允许转载,转载请保留全文! [请先阅读][说明&总目录]http://www.cnblogs.com/tbcaaa8/p/4415055.html 1. 梯度下降法 (Gradien ...
- 【数据分析】线性回归与逻辑回归(R语言实现)
文章来源:公众号-智能化IT系统. 回归模型有多种,一般在数据分析中用的比较常用的有线性回归和逻辑回归.其描述的是一组因变量和自变量之间的关系,通过特定的方程来模拟.这么做的目的也是为了预测,但有时也 ...
- 线性回归,逻辑回归,神经网络,SVM的总结
目录 线性回归,逻辑回归,神经网络,SVM的总结 线性回归,逻辑回归,神经网络,SVM的总结 详细的学习笔记. markdown的公式编辑手册. 回归的含义: 回归就是指根据之前的数据预测一个准确的输 ...
- 【Coursera】线性回归和逻辑回归
一.线性回归 1.批量梯度下降法 每次对参数进行一次迭代时,都要扫描一遍输入全集 算法可以收敛到局部最优值 当迭代多次之后,每次迭代参数的改变越小 2.随机梯度下降法 对于一个输入样本,对参数进行一次 ...
- 线性回归,感知机,逻辑回归(GD,SGD)
线性回归 线性回归是一个回归问题,即用一条线去拟合训练数据 线性回归的模型: 通过训练数据学习一个特征的线性组合,以此作为预测函数. 训练目标:根据训练数据学习参数(w1,w2, ... , wn,b ...
- Spark MLlib回归算法------线性回归、逻辑回归、SVM和ALS
Spark MLlib回归算法------线性回归.逻辑回归.SVM和ALS 1.线性回归: (1)模型的建立: 回归正则化方法(Lasso,Ridge和ElasticNet)在高维和数据集变量之间多 ...
- 机器学习(三)—线性回归、逻辑回归、Softmax回归 的区别
1.什么是回归? 是一种监督学习方式,用于预测输入变量和输出变量之间的关系,等价于函数拟合,选择一条函数曲线使其更好的拟合已知数据且更好的预测未知数据. 2.线性回归 于一个一般的线性模型而言,其 ...
随机推荐
- 【BJOI2019】光线 模拟
题目大意:有一束光线要依次穿过$n$块玻璃. 第i块玻璃的透射率为$a_i$,反射率为$b_i$. 问你有多少光能最终穿过所有玻璃. 数据范围:$n≤5\times 10^5$,答案对$9982443 ...
- 如何在IDEA里给大数据项目导入该项目的相关源码(博主推荐)(类似eclipse里同一个workspace下单个子项目存在)(图文详解)
不多说,直接上干货! 如果在一个界面里,可以是单个项目 注意:本文是以gradle项目的方式来做的! 如何在IDEA里正确导入从Github上下载的Gradle项目(含相关源码)(博主推荐)(图文详解 ...
- Spring Boot + Spring Cloud 实现权限管理系统 后端篇(十五):系统服务监控
系统服务监控 新建监控工程 新建Spring Boot项目,取名 kitty-monitor,结构如下. 添加项目依赖 添加 spring boot admin 的相关依赖. pom.xml < ...
- Feign使用Hystrix
Feign使用Hystrix开发步骤 1.导入依赖spring-cloud-starter-hystrix 2.消费启动类开启@EnableCircuitBreaker 3.配置yml文件feign. ...
- 深度学习之PyTorch实战(1)——基础学习及搭建环境
最近在学习PyTorch框架,买了一本<深度学习之PyTorch实战计算机视觉>,从学习开始,小编会整理学习笔记,并博客记录,希望自己好好学完这本书,最后能熟练应用此框架. PyTorch ...
- Linux卸载搭建环境
本章内容 卸载Apache PHP MySQL 卸载Apache 查看apache安装版本 $ apachectl -v 查看安装httpd相关软件包(红色部分) sudo yum list inst ...
- [Codeforces 1016F]Road Projects
Description 题库链接 给你一棵 \(n\) 个节点的树,定义 \(1\) 到 \(n\) 的代价是 \(1\) 到 \(n\) 节点间的最短路径的长度.现在给你 \(m\) 组询问,让你添 ...
- shell的编程结构体(函数、条件结构、循环结构)
bash&shell系列文章:http://www.cnblogs.com/f-ck-need-u/p/7048359.html 1.1 shell函数 在shell中,函数可以被当作命令一样 ...
- LinQ是什么?
•LINQ(发音:Link)是语言级集成查询(Language INtegrated Query) •LINQ是一种用来进行数据访问的编程模型,使得.NET语言可以直接支持数据查询 •LINQ的目标是 ...
- 探秘小程序(10):分享功能+webview
场景: 小程序页面用webview嵌入了h5页面,h5页面需要与小程序进行交互,h5页面内容不同,分享的链接也不一样 分享功能: 小程序的分享功能即用户点击小程序右上角,转发功能页面.可以指定分享卡片 ...
