n皇后问题_回溯法

具体问题如下图

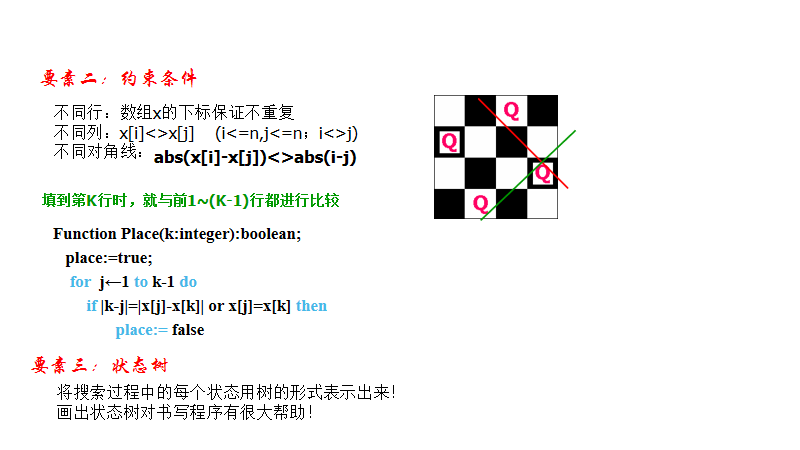
先看一下4*4的回溯过程

程序结束条件： 一组解：设标志，找到一解后更改标志，以标志做为结束循环的条件。 所有解：k=0

判断约束函数判断第k个后能不能放在x[k]处 两个皇后不能放在统一斜线上： 若2个皇后放置的位置分别是（i,j）和（k,l）, 且 i-j = k -l 或 i+j = k+l，则说明这2个皇后处于同一斜线上。

下面是利用递归和非递归实现的代码

 #include<bits/stdc++.h>
 using namespace std;
 int n;
 int x[];
 int sum=;

 /*
 判断第k个后能不能放在x[k]处
 两个皇后不能放在统一斜线上：
 若2个皇后放置的位置分别是（i,j）和（k,l）,
 且 i-j = k -l 或 i+j = k+l，则说明这2个皇后处于同一斜线上。
 */
 void output(){
     cout << "第" <<sum << "种放置方法为：" << endl;
  for(int i=;i<=n;i++){
     cout << "(" <<i << "," << x[i] << ")" << endl;
  }

 }
 int place(int k){
    for(int j=;j<k;j++){
     if(x[j]==x[k] || abs(x[j]-x[k])== abs(j-k))
         return ;
    }
    return ;
 }
 void BackTrace(int t,int n){//递归
     if(t>n){////如果t>n说明已经完成一次放置
         sum++;
         output();
     }
     else{
         for(int i=;i<=n;i++){
            x[t]=i;
            if(place(t)){// //可以放在i位置处，则继续搜索
             BackTrace(t+,n);
            }
         }

     }
 }

 void BackTrace1(int n){//非递归
    int k;
    x[]=;
    k=;
    while(k>=){
     x[k]+=;////先放在第一个位置
     while((x[k]<=n && !(place(k)))){//如果不能放
         x[k]++;//  //放在下一个位置
     }
     if(x[k]<=n){
         if(k==n){// //如果已经放完了n个皇后
             sum++;
             output();
         }
         else{//  //没有处理完，让k自加，处理下一个皇后
             k++;
             x[k]=;
         }
     }else{// 当前无法完成放置，则进行剪枝，回溯回去，回到第k-1步
       k--;
     }
    }
 }
 int main()
 {
     memset(x,,sizeof(x));
     cin >> n;
     cout << n << "皇后的放置方法为" << endl;
     //BackTrace(1,n);
     BackTrace1(n);
     return ;
 }

运行结果如下

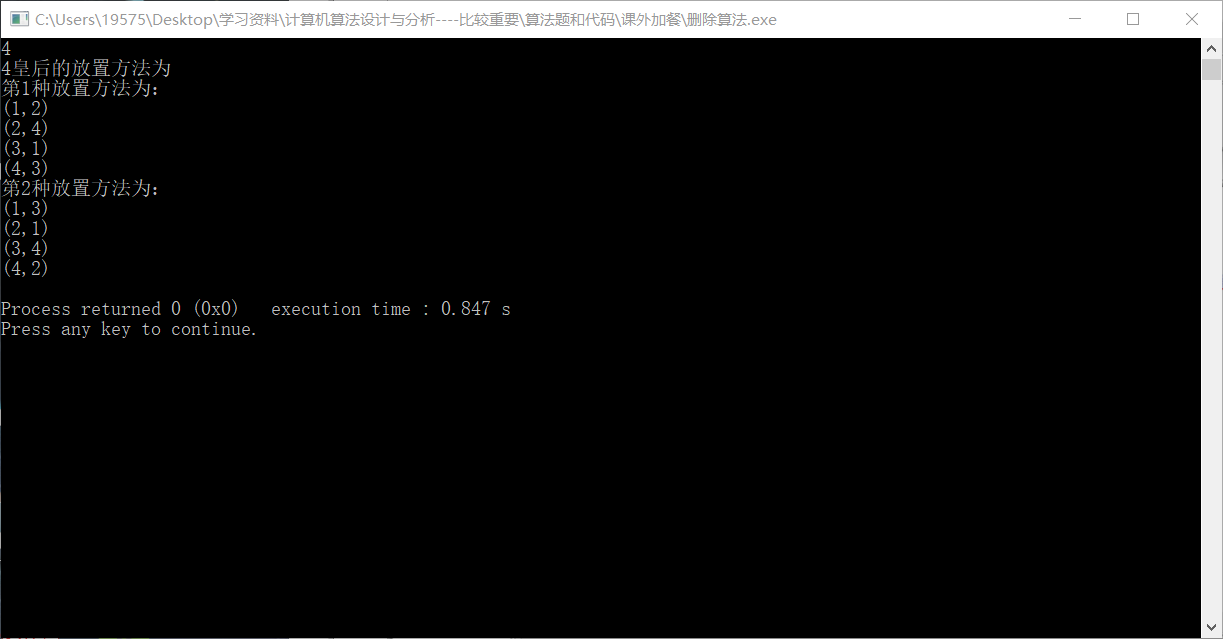
皇后个数要大于3才有可行结