dinic 算法基本思想及其模板

“网络流博大精深”—sideman语

一个基本的网络流问题
感谢WHD的大力支持

最早知道网络流的内容便是最大流问题，最大流问题很好理解：

解释一定要通俗!

如右图所示,有一个管道系统,节点{1,2,3,4},有向管道{A,B,C,D,E},即有向图一张. [1]是源点,有无限的水量,[4]是汇点,管道容量如图所示.试问[4]点最大可接收的水的流量?

这便是简单的最大流问题,显然[4]点的最大流量为50

死理性派请注意:流量是单位时间内的,总可以了吧!

然而对于复杂图的最大流方法是什么呢,有EK,Dinic,SAP,etc.下面介绍Dinic算法(看代码的直接点这)

Dinic 算法

Dinic算法的基本思路:

根据残量网络计算层次图。

在层次图中使用DFS进行增广直到不存在增广路

重复以上步骤直到无法增广

引自NOCOW,相当简单是吧…

小贴士:

一般情况下在Dinic算法中,我们只记录某一边的剩余流量.

残量网络:包含反向弧的有向图,Dinic要循环的,每次修改过的图都是残量网络,
层次图:分层图,以[从原点到某点的最短距离]分层的图,距离相等的为一层,(比如上图的分层为{1},{2,4},{3})
DFS:这个就不用说了吧…
增广 :在现有流量基础上发现新的路径,扩大发现的最大流量(注意:增加量不一定是这条路径的流量,而是新的流量与上次流量之差)
增广路:在现有流量基础上发现的新路径.(快来找茬,和上一条有何不同?)
剩余流量:当一条边被增广之后(即它是增广路的一部分,或者说增广路通过这条边),这条边还能通过的流量.
反向弧:我们在Dinic算法中,对于一条有向边,我们需要建立另一条反向边(弧),当正向(输入数据)边剩余流量减少I时,反向弧剩余流量增加I

Comzyh的较详细解释(流程) :

Dinic动画演示

用BFS建立分层图注意:分层图是以当前图为基础建立的,所以要重复建立分层图
用DFS的方法寻找一条由源点到汇点的路径,获得这条路径的流量I 根据这条路径修改整个图,将所经之处正向边流量减少I,反向边流量增加I,注意I是非负数
重复步骤2,直到DFS找不到新的路径时,重复步骤1

注意(可以无视):

Dinic(其实其他的好多)算法中寻找到增广路后要将反向边增加I
Dinic中DFS时只在分层图中DFS，意思是说DFS的下一个节点的Dis(距源点的距离)要比自己的Dis大1,例如在图1中第一个次DFS中,1->2->4 这条路径是不合法的,因为Dis[2]=1;Dis[4]=1;
步骤2中“获得这条路径的流量I “实现:DFS函数有参量low,代表从源点到现在最窄的(剩余流量最小)的边的剩余流量,当DFS到汇点是,Low便是我们要的流量I

对于反向弧(反向边)的理解:

这一段不理解也不是不可以,对于会写算法没什么帮助,如果你着急,直接无视即可.
先举一个例子(如右图):

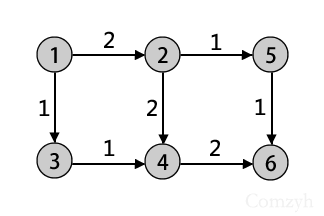必须使用反向弧的流网络

在这幅图中我们首先要增广1->2->4->6,这时可以获得一个容量为2的流,但是如果不建立4->2反向弧的话,则无
法进一步增广,最终答案为2,显然是不对的,然而如果建立了反向弧4->2,则第二次能进行
1->3->4->2->5->6的增广,最大流为3.

Comzyh对反向弧的理解可以说是”偷梁换柱“,请仔细阅读:
在上面的例子中,我们可以看出,最终结果是1->2->5->6和1->2->4->6和
1->3->4->6.当增广完1->2->4->5(代号A)后,在增广
1->3->4->2->5->6(代号B),相当于将经过节点2的A流从中截流1(总共是2)走2->5>6,而不走2->4>6了,同时B流也从节点4截流出1(总共是1)走4->6而不是4->2->5->6,相当于AB流做加法.

简单的说反向弧为今后提供反悔的机会,让前面不走这条路而走别的路.

Alwa同学非要我给他的文章加一个链接,大家可以看看他的文章: 有关网络流中的反向弧和增广路

Dinic算法的程序实现

最大流算法一直有一个入门经典题:POJ 1273 或者是UCACO 4_2_1 来自NOCOW(中文) 这两个是同一个题

给出这道题的代码

#include<stdio.h>

#include<string.h>

#include<iostream>

#include<queue>

#include<algorithm>

using namespace std;

int edge[][];//邻接矩阵

int dis[];//距源点距离,分层图

int start,end;

int m,n;//N:点数;M,边数

int bfs(){

   memset(dis,-,sizeof(dis));//以-1填充

   dis[]=;

   queue<int>q;

   q.push(start);

   while(!q.empty()){

        int u=q.front();

        q.pop();

        for(int i=;i<=n;i++){

            if(dis[i]<&&edge[u][i]){

                dis[i]=dis[u]+;

                q.push(i);

            }

        }

   }

   if(dis[n]>)

    return ;

   else

    return ;//汇点的DIS小于零,表明BFS不到汇点

}

//Find代表一次增广,函数返回本次增广的流量,返回0表示无法增广

int find(int x,int low){//Low是源点到现在最窄的(剩余流量最小)的边的剩余流量

    int a=;

    if(x==n)

        return low;//是汇点

    for(int i=;i<=n;i++){

        if(edge[x][i]>&&dis[i]==dis[x]+&&//联通,,是分层图的下一层

           (a=find(i,min(low,edge[x][i])))){//能到汇点(a <> 0)

            edge[x][i]-=a;

            edge[i][x]+=a;

            return a;

           }

    }

    return ;

}

int main(){

   while(scanf("%d%d",&m,&n)!=EOF){

       memset(edge,,sizeof(edge));

       for(int i=;i<=m;i++){

          int u,v,w;

          scanf("%d%d%d",&u,&v,&w);

          edge[u][v]+=w;

       }

       start=;

       end=n;

       int ans=;

       while(bfs()){//要不停地建立分层图,如果BFS不到汇点才结束

        ans+=find(,0x7fffffff);//一次BFS要不停地找增广路,直到找不到为止

       }

       printf("%d\n",ans);

   }

   return ;

}