培训补坑（day1：最短路&two-sat）

经过12天的滚粗，终于迎来了暑期培训的结尾啦QAQ

结业考才考了90分，真是对不起孙爷（孙爷请收下我的膝盖）

orz小粉兔怒D rank 1 获得小粉兔一只QAQ

由于这次12天的培训题目又比较多，算法较难，所以只能等到课程结束之后再来补坑了。

现在开始补坑（BEGIN大工程！！）

day1主要知识：最短路+two-sat

首先是最短路：

对于最短路目前我们大部分人用的就是两种算法：

一、dijkstra算法：

dij算法基于的思想就是每次从所有已拓展的节点相连的未拓展的节点取出一个dis值最小的节点加入集合，直到找到所有点的最短路

这种做法唯一的优点就是跑的比spfa快，但是这种算法不能处理负权边。而且也只是处理单源最短路问题

对于找到dis最小值的点有两种方法，第一种就是n^2暴力枚举点，但是这样太慢，所以通常我们把点放入优先队列中或者是堆中优化复杂度

然后我们贴个图来讲解一下具体做法：

一开始的时候没有一个点在集合中：

接下来一号节点入队

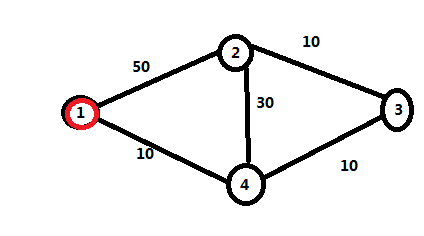
我们发现4号节点离1号节点最近，4号节点入队。

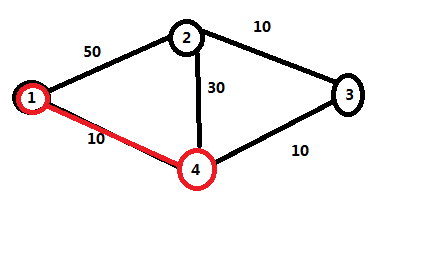
接下来我们发现3号节点离1号节点和4号节点最近，3号节点入队

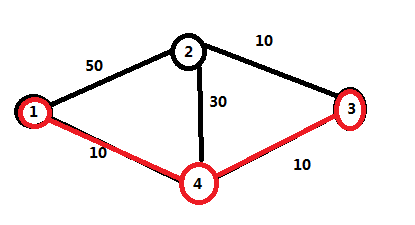
最后二号节点入队

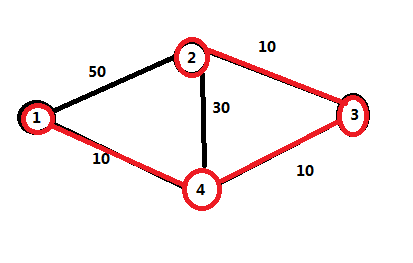
至此，最短路结束。

下面附上例题：

给定N个节点，M条无向边的图，求1号节点到N号节点次短路的长度

备注：次短路是长度大于最短路中最短的路径

——————————————我是分割线——————————————

这道题目显然是单源最短路问题，只不过我们我们找到一个点看能不能更新最短路，如果能就更新，否则再和次短路进行比较。注意这题最短路和次短路不能相同，所以如果一个点的dis值与最短路的值相同要跳过才可以。

下面附上代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define MN 200005
#define M 5005
using namespace std;
int head[M],d1[M],d2[M],n,m,num;
struct e{
    int to,next,w;
}g[MN];
void ins(int u,int v,int val){g[++num].next=head[u];head[u]=num;g[num].to=v;g[num].w=val;}
void insw(int u,int v,int w){ins(u,v,w);ins(v,u,w);}
void swap(int &a,int &b){a^=b;b^=a;a^=b;}
struct edge{
    int to,value;
    edge(int to,int value):to(to),value(value) {}
    friend bool operator <(edge a,edge b){
        return a.value>b.value;
    }
};
priority_queue<edge>q;
void dij(){
    d1[]=;q.push(edge(,));
    while(!q.empty()){
        edge tmp=q.top();q.pop();if(tmp.value>d2[tmp.to])continue;
        for(int i=head[tmp.to];i;i=g[i].next){
            int dd=tmp.value+g[i].w;
            if(dd==d1[g[i].to])continue;
            if(dd<d1[g[i].to]){
                swap(dd,d1[g[i].to]);
                q.push(edge(g[i].to,d1[g[i].to]));
            }
            if(dd<d2[g[i].to]){
                swap(dd,d2[g[i].to]);
                q.push(edge(g[i].to,d2[g[i].to]));
            }
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);memset(d1,0x3f,sizeof(d1));memset(d2,0x3f,sizeof(d2));
    int x,y,val;
    for(int i=;i<=m;i++)scanf("%d%d%d",&x,&y,&val),insw(x,y,val);
    dij(),printf("%d\n",d2[n]);
    return ;
}

二、spfa

spfa的原理与dij有点相像，不过它处理的是多元最短路问题，可以有多个起点，它的基础算法就是松弛操作，只要目前在队中的节点有一条边能使到达其他点的dis值更小，就更新dis值，并且让被更新的节点入队，由于一个点最多入队n次，所以最坏复杂度是O(nm),不过有一些优化可以让这个算法变得更快，这个我们下面讲。

还是刚才那张图

首先1号节点入队（假设只有一个源）

然后我们发现与一号节点相连的点有二号和四号节点。更新dis[2]=50,dis[4]=10，2，4号节点入队。1号节点出对。

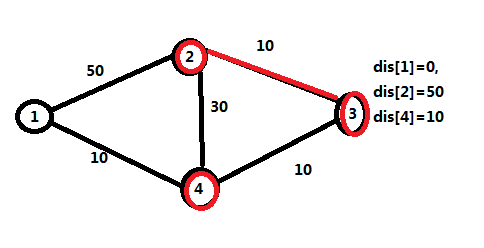
然后我们看到了三号节点没有进过队,它的dis值是inf于是3号节点入队，2号节点出队

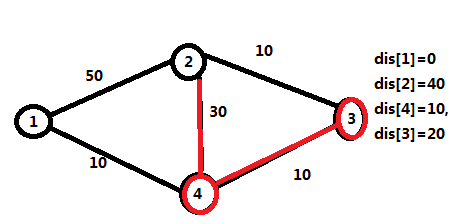
我们发现4号节点能更新2号节点和3号节点，更新完后4号节点出队

最后我们发现3号节点能够更新2号节点，更新完3号节点出队，最短路结束。

在附上代码之前讲2个优化。

1、SLF优化

因为我们看到上图进行了多次松弛操作，所以复杂度较高。

不过如果我们调换一下入队顺序，比如原来的入队顺序是2 3 4节点

如果我们改成4 3 2节点，我们就会发现没有松弛操作了。一次就得出了正解。

这就是SLF优化。如果当前找到的v（边的终点）节点的dis值比队头元素的dis值更小，那么我们就把这个点放在队头。这样能优化30%左右，并且在本图中效果最为明显。

2、循环队列优化

再讲一个不是优化的优化，就是循环队列。因为在一个队列中最多只能同时存在n（n为点的总数）个元素，所以我们可以将队列循环使用，节省空间。

下面直接附上代码

void spfa(){
    memset(vis,,sizeof(vis));
    for(int i=;i<=n;i++)dis[i]=inf;
    dis[T]=;vis[T]=;int h=,t=;que[]=T;
    while(h!=t){
        int tmp=que[(++h)%=MN];
        for(int i=head[tmp];i;i=g[i].next)
            if(g[i^].w&&dis[g[i].to]-dis[tmp]+g[i].c>eps){
                dis[g[i].to]=dis[tmp]-g[i].c;
                if(!vis[g[i].to]){
                    vis[g[i].to]=;
                    if(dis[g[i].to]<dis[que[(h+)%MN]])que[h]=g[i].to,h=(h-+MN)%MN;
                    else que[(++t)%=MN]=g[i].to;
                }
            }vis[tmp]=;
    }
}

接下来我们讲讲第二个大块two-set

two-sat问题就是这样：对于一个事件你只有两种选择，选，或者不选。

而且对于两个事件间还有一些约束条件，如A、B中至少要选一个。

而two-sat算法就是将这些限制条件转换为不同状态之间的边，然后通过染色来判断满足条件的情况是否存在的。

two-sat最重要的方法就是将一个点拆成2个，一个是选，一个是不选。

举个例子：

假如A、B之间我至少要选一个

那么反之，如果我A没选，那么B一定选

如果我B没选，A我一定选

那么我只要在非A与B，非B与A之间连一条单向边就好了。（非表示不选）

其他的条件同理

下面直接附上例题代码（由于是英文大家就自己理解啦。。我偷懒一下下QAQ）

#include<cstdio>
#include<cstring>
#define MN 100005
using namespace std;
int n,m,tot,x,y,num,top;
int age[MN],vis[MN*],stack[MN],head[MN*];
struct edge{
    int to,next;
}g[MN*];
void ins(int u,int v){g[++num].next=head[u];head[u]=num;g[num].to=v;}
bool kind(int now){return age[now]*n<tot;}
bool dfs(int u){
    if(vis[u^])return false;
    if(vis[u])return true;
    vis[u]=true;stack[top++]=u;
    for(int i=head[u];i;i=g[i].next){
        if(!dfs(g[i].to))return false;
    }
    return true;
}
bool t_sat(){
    memset(vis,,sizeof(vis));
    for(int i=;i<*n;i+=){
        if(vis[i]||vis[i^])continue;
        top=;
        if(!dfs(i)){
            while(top)vis[stack[--top]]=;
            if(!dfs(i^))return false;
        }
    }
    return true;
}
int main(){
    while(scanf("%d%d",&n,&m)!=EOF){
        if(n==&&m==)break;
        memset(g,,sizeof(g));
        memset(head,,sizeof(head));
        memset(stack,,sizeof(stack));
        num=tot=;
        for(int i=;i<n;i++)scanf("%d",&age[i]),tot+=age[i];
        for(int i=;i<=m;i++){
            scanf("%d%d",&x,&y);
            x--,y--;
            if(kind(x)==kind(y)){
                ins(x<<,y<<|);
                ins(y<<,x<<|);
            }
            ins(x<<|,y<<);
            ins(y<<|,x<<);
        }
        if(t_sat()){
            for(int i=;i<*n;i+=){
                if(!vis[i]){
                    printf("C\n");continue;
                }
                else if(kind(i/))printf("B\n");
                else printf("A\n");
            }
        }else printf("No solution.\n");
    }
}