@codeforces - 793G@ Oleg and chess

@description - translation@
@solution@
@accepted code@
@details@

@description - translation@

给定一个 n*n 的棋盘，并划定一些不能放棋子的矩形区域。

现在要在棋盘上放最多的车（读作 ju），使得这些车两两之间不会攻击。

input：

第一行整数 n ——棋盘边长（1 <= n <= 10000）。

第二行整数 q ——划定的矩形个数（0 <= q <= 10000）。

接下来 q 行，每一行都是 x1, y1, x2, y2（1 <= x1 <= x2 <= n， 1 <= y1 <= y2 <= n），描述矩阵的左下角与右上角。

保证矩形两两不会相交。

output：

输出最多的车的个数。

sample input：

5

5

1 1 2 1

1 3 1 5

4 1 5 5

2 5 2 5

3 2 3 5

sample output：

3

sapmle explain：

如图。

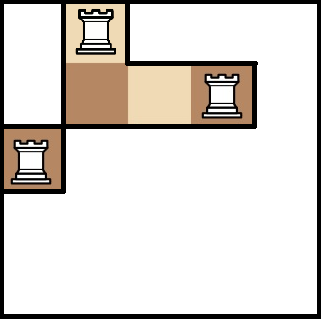
@solution@

一道网络流题。

一道建模极其简单，建图极其恶心的网络流题。

@part - 1@

考虑建模。棋盘是一个很经典的二分图，可以是黑白染色建模，也可以是行列建模。考虑到车的攻击方式是同行同列攻击，所以我们选择后者。

假如某一个格子(i, j)没有被划定不能放车，我们就第 i 行与第 j 列连边。再跑一个最大匹配就可以求出最多放置多少车了。

然而显然是会 TLE 的，而且还会 T 的很惨，惨兮兮。

@part - 2@

优化建图的话，因为划定的是规则的矩形，所以我们考虑用线段树来优化建图。

如图是一个内部完全没有限制的矩形，我们用行、列两棵线段树将它的两个横竖的边界拆成log n条线段树上的线段：

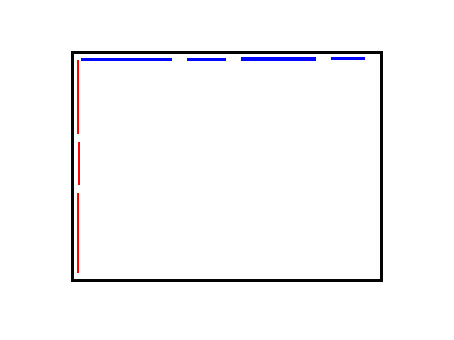
然后横着的和竖着的两两连边，连 log^2 n 条边【图片略鬼畜】：

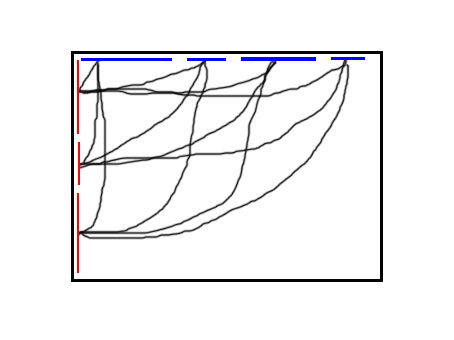
这样就处理完了一个没有限制的矩形。

最后：两棵线段树的底层端点，一棵连 S，一棵连 T，容量都为 1。线段树内部的父子连容量为 inf 的边。

@part - 3@

然而问题又来了：我们给定的是限制的矩形区域。

所以，我们必须把原棋盘切割成若干个内部没有限制的矩形，才能运用上面所提到的优化。

怎么切？下面是一个比较显然的思路：

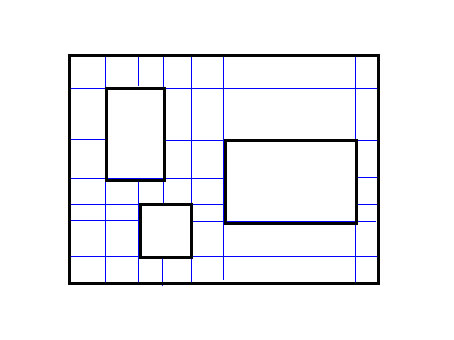
即对于每一个矩形，它的上下左右边界往两边割。

然而，如果下面这个图……

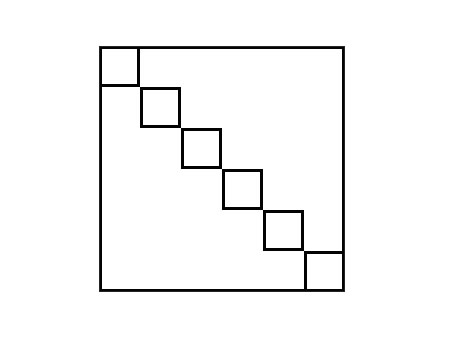
直接卡成 O(n^2)。

我们发现上面的那种切割方法，有很多小矩形是可以合并成大矩形。所以我们优化一下切割方法：

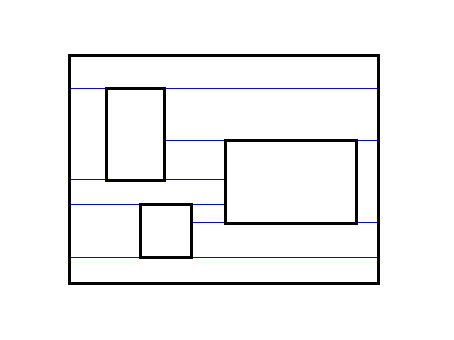
即上下边界往两边切，遇到其他矩形的边界或棋盘的边界，则停下来。

这样切，可以证明最多只会分出 4*n 个矩形。

怎么证明呢？【感性理解】每一个矩形的上下边界向左右各引一条线，一共 4 条线，每条线可以把一个矩形切割成两个矩形，相当于多增加了 4 个矩形。所以最多 4n 个矩形。

@part - 4@

OK 现在来看看怎么实现切割。

我们用扫描线算法，从左往右扫描。对于每一行，维护扫描线左边距离扫描线最近的矩形边界。如图，我们维护的就是左边的那弯弯曲曲的曲线：

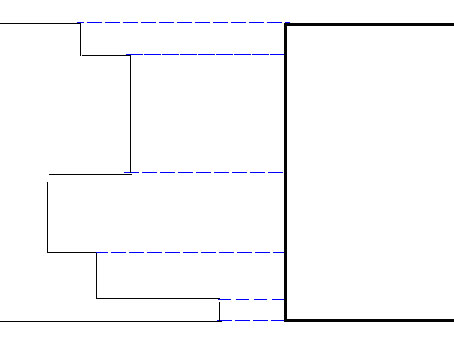
假如遇到矩形左边界，我们就从这个矩形的上边界开始往下暴力遍历（对你没听错就是暴力遍历，这样的确是 O(n^2) 的，但是其实 n 不大，对吧）。假如遇到不平坦的地方（对应到代码中就是相邻两行维护的东西不相等），则说明又产生了新的矩形。我们就进行线段树建图。

假如遇到矩形右边界，更新 “扫描线左边距离扫描线最近的矩形边界”。

注意，这个算法是基于矩阵不相交的前提的。

@accepted code@

口胡完毕。至于代码量，我不清楚我不知道，大家自己慢慢调，总会调出来的 qwq。

#include<cstdio>

#include<vector>

#include<algorithm>

using namespace std;

const int MAXN = 10000;

const int MAXM = 100000;

const int MAXK = 2000000;

const int INF = (1<<30);

struct FlowGraph{

	struct edge{

		int to, cap, flow;

		edge *nxt, *rev;

	}edges[2*MAXK + 5], *adj[MAXM + 5], *ecnt=&edges[0];

	int S, T, d[MAXM + 5], vd[MAXM + 5];

	void addedge(int u, int v, int c) {

		edge *p = (++ecnt);

		p->to = v, p->cap = c, p->flow = 0;

		p->nxt = adj[u], adj[u] = p;

		edge *q = (++ecnt);

		q->to = u, q->cap = 0, q->flow = 0;

		q->nxt = adj[v], adj[v] = q;

		p->rev = q, q->rev = p;

	}

	int aug(int x, int tot) {

		if( x == T ) return tot;

		int mind = T+1, sum = 0;

		for(edge *p=adj[x];p!=NULL;p=p->nxt) {

			if( p->cap > p->flow ) {

				if( d[p->to] + 1 == d[x] ) {

					int del = aug(p->to, min(tot-sum, p->cap-p->flow));

					p->flow += del, p->rev->flow -= del, sum += del;

					if( d[S] == T+1 ) return sum;

					if( sum == tot ) return sum;

				}

				mind = min(mind, d[p->to]);

			}

		}

		if( sum == 0 ) {

			vd[d[x]]--;

			if( vd[d[x]] == 0 )

				d[S] = T+1;

			d[x] = mind + 1;

			vd[d[x]]++;

		}

		return sum;

	}

	int max_flow() {

		int flow = 0;

		while( d[S] < T+1 )

			flow += aug(S, INF);

		return flow;

	}

}G;

int cnt = 0;

struct SegmentTree{

	int le, ri, num;

}t[2][4*MAXN + 5];

vector<int>v[2];

void build_segtree(int x, int l, int r, int n) {

	t[n][x].le = l, t[n][x].ri = r, t[n][x].num = (++cnt);

	if( l == r ) return ;

	int mid = (l + r) >> 1;

	build_segtree(x<<1, l, mid, n);

	build_segtree(x<<1|1, mid+1, r, n);

}

void build_edge_segtree(int x, int n) {

	if( t[n][x].le == t[n][x].ri ) {

		if( n == 0 ) G.addedge(G.S, t[n][x].num, 1);

		else G.addedge(t[n][x].num, G.T, 1);

	}

	else {

		if( n == 0 ) {

			G.addedge(t[n][x<<1].num, t[n][x].num, INF);

			G.addedge(t[n][x<<1|1].num, t[n][x].num, INF);

		}

		else {

			G.addedge(t[n][x].num, t[n][x<<1].num, INF);

			G.addedge(t[n][x].num, t[n][x<<1|1].num, INF);

		}

		build_edge_segtree(x<<1, n);

		build_edge_segtree(x<<1|1, n);

	}

}

void get_segment(int x, int l, int r, int n) {

	if( l <= t[n][x].le && t[n][x].ri <= r ) {

		v[n].push_back(t[n][x].num);

		return ;

	}

	if( l > t[n][x].ri || r < t[n][x].le )

		return ;

	get_segment(x<<1, l, r, n);

	get_segment(x<<1|1, l, r, n);

}

void build_edge_area(int x1, int y1, int x2, int y2) {

	if( x1 > x2 || y1 > y2 ) return ;

	v[0].clear(), v[1].clear();

	get_segment(1, x1, x2, 0);

	get_segment(1, y1, y2, 1);

	for(int i=0;i<v[0].size();i++)

		for(int j=0;j<v[1].size();j++)

			G.addedge(v[0][i], v[1][j], INF);

}

struct node{

	int le, ri;

	node(int _l=0, int _r=0):le(_l), ri(_r){}

};

vector<node>vec[MAXN + 5][2];

int left[MAXN + 5];

int main() {

	int n, q;

	scanf("%d%d", &n, &q);

	build_segtree(1, 1, n, 0); build_segtree(1, 1, n, 1); G.T = cnt + 1;

	build_edge_segtree(1, 0); build_edge_segtree(1, 1);

	for(int i=1;i<=q;i++) {

		int x1, y1, x2, y2;

		scanf("%d%d%d%d", &y1, &x1, &y2, &x2);

		vec[x1][0].push_back(node(y1, y2));

		vec[x2][1].push_back(node(y1, y2));

	}

	vec[n+1][0].push_back(node(1, n));

	for(int i=1;i<=n+1;i++) {

		for(int j=0;j<vec[i][0].size();j++) {

			int lst = vec[i][0][j].le;

			for(int k=vec[i][0][j].le+1;k<=vec[i][0][j].ri;k++)

				if( left[k] != left[k-1] )

					build_edge_area(left[k-1]+1, lst, i-1, k-1), lst = k;

			build_edge_area(left[vec[i][0][j].ri]+1, lst, i-1, vec[i][0][j].ri);

		}

		for(int j=0;j<vec[i][1].size();j++)

			for(int k=vec[i][1][j].le;k<=vec[i][1][j].ri;k++)

				left[k] = i;

	}

//注意我们必须要先处理矩形的左边再处理矩形的右边，不然遇到宽度为 1 的矩形就直接 GG 了。

	int ans = G.max_flow();

	printf("%d\n", ans);

}

@details@

一开始我写的从上往下的扫描线，结果发现 TLE 在 144th 组数据上。

气的我一怒之下把扫描线改成从左往右的。

然后……它就 AC 了？？？

听说机房里的另外一个人遇到了一样的情况，然后他把 isap 换成了 dinic 才过的。

好玄妙啊，果然是网络流。