洛谷p-1522又是Floyd

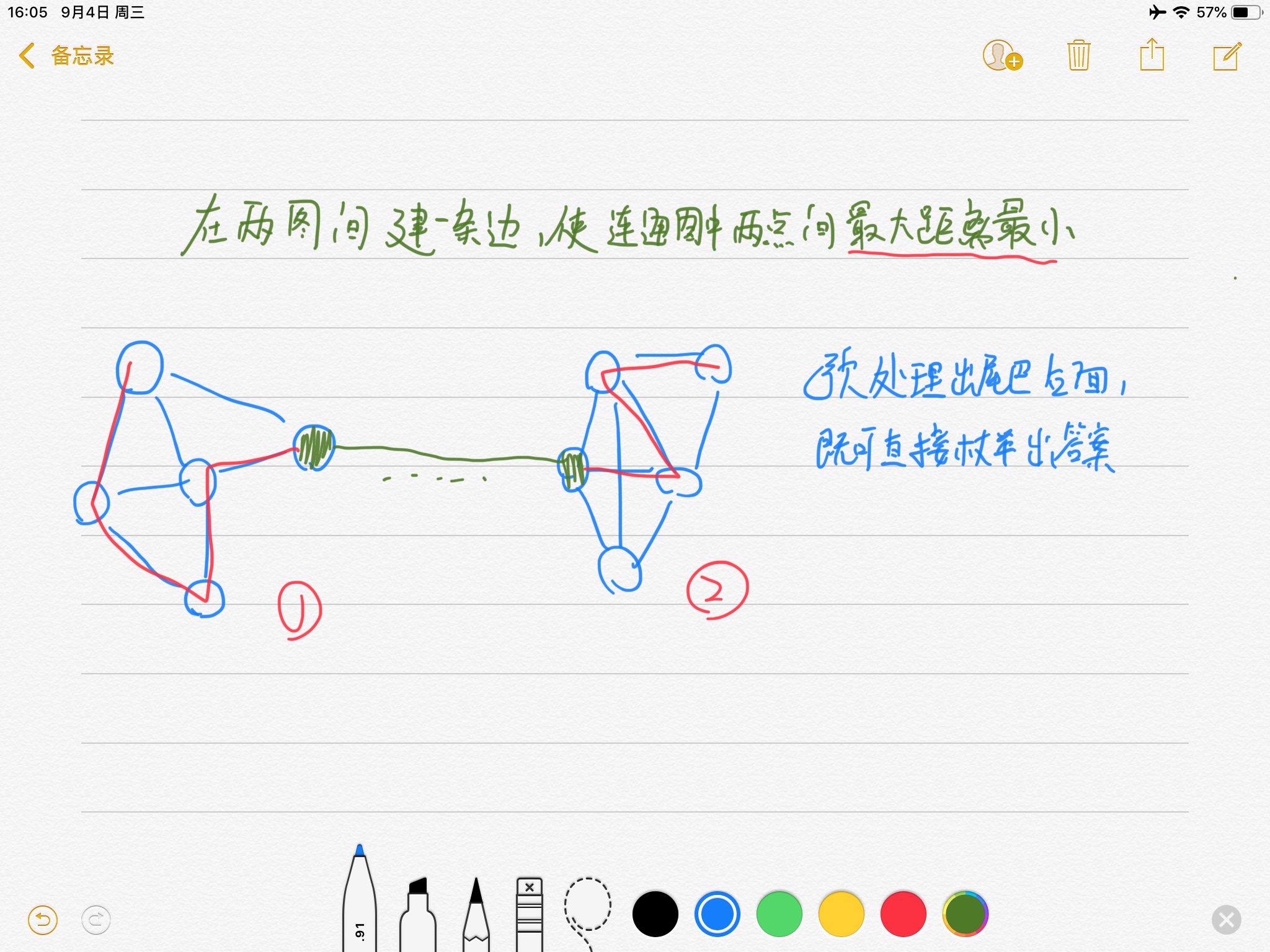
挺简单一个题，可惜当时没想到，有点巧妙丫！

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define maxn 255
using namespace std;
char list[maxn][maxn];
double map[maxn][maxn];
int vis[maxn];
int ins[maxn];
int n, m;
struct Node {
	double x;
	double y;
	double len;
}que[maxn];
double get(Node a, Node b) {
	return sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
}

int dfs(int x, int num) {
	ins[x] = num;
	vis[x] = 1;
	for (int i = 0; i < n; i++) {
		if (!vis[i] && list[x][i] == '1') dfs(i, num);
	}
	return 0;
}
void floyd() {
	for (int k = 0; k < n; k++) {
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				map[i][j] = min(map[i][j], map[i][k] + map[k][j]);
			}
		}
	}
}
int main() {
	scanf("%d", &n);
	for (int i =  0; i < n; i++) {
		scanf("%lf %lf", &que[i].x, &que[i].y);
	}
	for (int i = 0; i < n; i++) {
		scanf("%s", list[i]);
	}

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (list[i][j] == '0') map[i][j] = 1100000.0;
			else map[i][j] = get(que[i], que[j]);
		}
	}
	for (int i = 0; i < n; i++) map[i][i] = 0.0;
	floyd();
	int cnn = 0;
	for (int i = 0; i < n; i++) {
		if (!vis[i]) {
			cnn++;
			dfs(i, cnn);
		}
	}
	for (int i = 0; i < n; i++) {
		que[i].len = 0;
		for (int j = 0; j < n; j++) {
			if (ins[i] == ins[j]) {
				double len = map[i][j];
				que[i].len = max(que[i].len, len);
			}
		}
	}
	double ans = 1100000;

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (ins[i] != ins[j]) {
				double len = get(que[i], que[j]);
				len += que[i].len + que[j].len;
				ans = min(ans, len);
			}
		}
	}
	for (int i = 0; i < n; i++) {
		ans = max(que[i].len, ans);//特殊情况，原图自己就已经够大的了，没必要再加了
	}

	printf("%.6lf\n", ans);
	return 0;
}