poj 1655 Balancing Act 求树的重心【树形dp】

poj 1655 Balancing Act

题意：求树的重心且编号数最小

一棵树的重心是指一个结点u，去掉它后剩下的子树结点数最少。

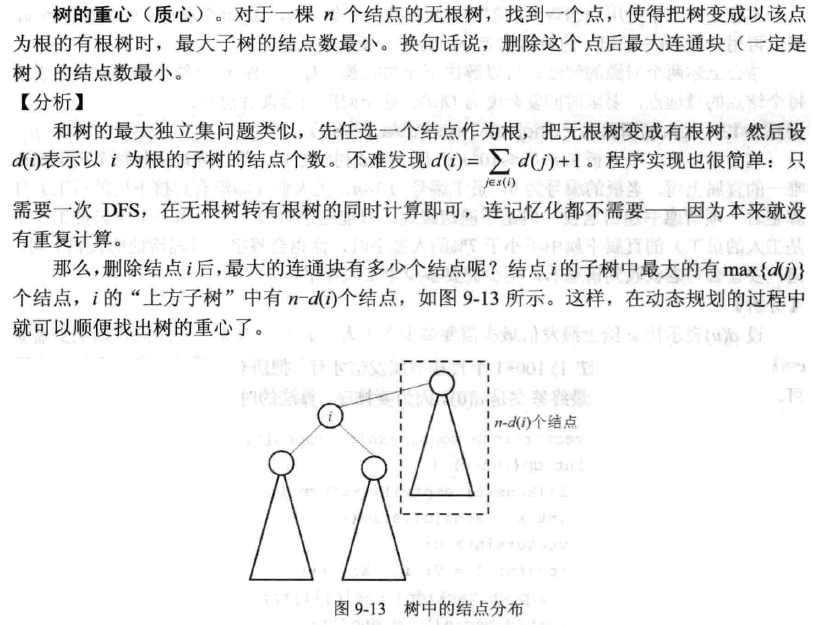
（图片来源： PatrickZhou 感谢博主）

看上面的图就好明白了，不仅要考虑当前结点子树的大小，也要“向上”考虑树的大小。

那么其它就dfs完成就行了，son[] 存以前结点为根的结点个数。

这是用邻接表写：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int maxn = ;
 const int INF =  << ;
 int head[maxn];
 int son[maxn];
 bool vis[maxn];
 int n,siz, cnt, num;
 struct Edge
 {
     int to, next;
 };
 Edge edge[maxn*];

 void Init()
 {
     memset(vis, , sizeof(vis));
     memset(head, -, sizeof(head));
     siz =num= INF;
     cnt = ;
 }

 void add(int u, int v)
 {
     edge[cnt].to = v;
     edge[cnt].next = head[u];
     head[u] = cnt++;
 }

 void dfs(int u)
 {
     vis[u] = ;
     son[u] = ;
     int tmp = ;
     for (int i = head[u]; i != -; i = edge[i].next)
     {
         int v = edge[i].to;
         if (!vis[v]) {
             dfs(v);
             son[u] += son[v];
             tmp = max(tmp, son[v]);
         }
     }
     tmp = max(tmp, n - son[u]);
     if (tmp < siz || (tmp == siz&&u < num)) {
         siz = tmp;
         num = u;
     }
 }

 int main()
 {
     int T;
     cin >> T;
     while (T--)
     {
         cin >> n;
         Init();
         for (int i = ; i < n; i++) {
             int u, v;
             cin >> u >> v;
             add(u, v);
             add(v, u);
         }
         dfs();
         cout << num << " " << siz << endl;
     }
     return ;
 }

这题用stl不超时：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<algorithm>
 using namespace std;
 const int maxn = ;
 const int INF =  << ;
 vector<int> tree[maxn];
 int son[maxn];
 int n, siz,num;

 void dfs(int u, int fa)
 {
     son[u] = ;
     int tmp = ;
     for (int i = ; i < tree[u].size(); i++) {
         int v = tree[u][i];
         if (v != fa) {
             dfs(v,u);
             son[u] += son[v];
             tmp = max(tmp, son[v]);
         }
     }
     tmp = max(tmp, n - son[u]);
     if ((tmp < siz) || (tmp == siz&&u > num)) {
         siz = tmp;
         num = u;
     }
 }

 int main()
 {
     int T;
     cin >> T;
     while (T--)
     {
         cin >> n;
         for (int i = ; i <= n; i++) tree[i].clear();
         for (int i = ; i < n; i++) {
             int u, v;
             cin >> u >> v;
             tree[u].push_back(v);
             tree[v].push_back(u);
         }
         num = , siz = INF;
         dfs(, -);
         cout << num << " " << siz << endl;
     }
     return ;
 }