纪中18日c组模拟赛

T2 GMOJ2127. 电子表格

(File IO): input:excel.in output:excel.out

时间限制: 1000 ms  空间限制: 262144 KB  具体限制  

Goto ProblemSet

题目描述

也许你用过Microsoft Excel之类的电子制表软件，这类软件最令人称道的就是强大的公式计算功能。现在希望你也来实现一个具有最基本功能的电子制表软件。表格共有m列(0 < m • 26)，从左到右依次用A到Z的大写英文字母表示；有n行(0 < n <100)，从上到下依次用1到100的整数表示。这样，每一个单元格的位置就可以唯一地用它所在的列和行表示出来，例如从左到右第3列，从上到下第5行的单元格就可以用“ C5”来表示（注意，这里字母和数字中间没有空格）。
现在对表格进行了一系列的操作，这些操作主要就是赋值和查询。定义操作的输入规则
如下：

• 每个操作占一行，根据操作类型的不同，每行中可能有二至四个用空格隔开的“单词”；
• 每行的第一个单词指定了该操作涉及的单元格的位置；
• 每行的第二个单词指定了相应的操作，可能是： input,output,sum,avg
• 　　(1).如果第二个单词是input，表示接下来的一个整数是要赋予该单元格的值，这个值是不超过1000的正整数
• 　　(2).如果第二个单词是output，表示你需要在输出文件中输出这个单元格当前的值
• 　　(3).如果第二个单词是sum，表示接下来输入的两个单词定义了一个矩形区域，该单元格的值就应该恒为这个矩形区域中所包含的单元格的值的和，直到该单元格被重新定义
• 　　(4).如果第二个单词是avg，表示接下来输入的两个单词定义了一个矩形区域，该单元格的值就应该恒为这个矩形区域中所包含的单元格的值的算术平均数，直到该单元格被重新定义；
• “输入的两个单词定义了一个矩形区域”是指输入一个矩形区域的左上角和右下角的单元格的位置，这样就唯一确定了这个矩形区域；
• 所有时刻，每个单元格的值均为整数，如果不是，则向下取整；
• 如果某个单元格的值没有在上文定义，则它的值默认为0；
• 不会出现循环定义的情况；
• 在操作过程中所有单元格的值不超过2³¹-1。

输入

第一行输入两个用空格隔开的正整数m和n，分别代表表格的列数和行数。
第二行输入一个正整数s，表示操作的总数。
以下s行每行输入一个操作，具体格式参见问题描述。

输出

对于输入数据的每一个“ output”操作输出一行结果。因此，输出文件的行数等于输入文
件中“ output”操作的个数。

样例输入

3 5
5
A1 input 100
B2 input 200
C3 sum A1 C2
C5 avg B2 C4
C5 output

样例输入

83

数据范围限制

对于30%的数据， m; n; s <= 10；
对于100%的数据， m <= 26， n < =100， s <=100。

Solution

当我看到上面的数据范围限制时，心中无比的开心……

n²暴力，是个地球人都不会TLE吧？

嗯，没错，我Wonderful Answer了了了了了……

本地过，样例太简单了吧……

每次有新的定义时直接计算该单元格的值是错误的，因为sum 和avg 的单元格必须随时更新（题目说明了这样的单元格必须恒等于要求的数值和或平均数）。

神奇的wrong！我也知道呀！

but我用了个栈来存储指令，每次操作后都让它执行一遍的……

大概是要把输入变代码吧。

没错，本地是过了，但是0分呐！

Code

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<map>
 #include<set>
 #include<vector>
 #include<algorithm>
 #define IL inline
 using namespace std;
 struct node{
     int x,y;//输出单元格
     bool avg;//0->求和    1->求平均数
     int x1,x2,y1,y2;//计算对象
 }order[];
 int tail=;
 string str;
 int m,n,s;
 int array[][];
 int main()
 {
 //    freopen("excel.in","r",stdin);
 //    freopen("excel.out","w",stdout);
     cin>>m>>n>>s;
     int x,y;
     while(s--)
     {
         x=getchar();
         while(x<'A'||x>'Z'){
             x=getchar();
         }
         x-='A';
         y=getchar()-'';
         cin>>str;
         int i=;
         bool flag=;
         do{
             switch(str[i]){
                 case 'i':{
                     int value;
                     cin>>value;
                     array[x][y]=value;
                     break;
                 }
                 case 'o':{
                     cout<<array[x][y]<<endl;
                     break;
                 }
                 case 's':{
                     order[tail].x=x;
                     order[tail].y=y;

                     order[tail].avg=;

                     order[tail].x1=getchar();
                     while(order[tail].x1<'A'||order[tail].x1>'Z') order[tail].x1=getchar();
                     order[tail].x1-='A';
                     order[tail].y1=getchar()-'';

                     order[tail].x2=getchar();
                     while(order[tail].x2<'A'||order[tail].x2>'Z') order[tail].x2=getchar();
                     order[tail].x2-='A';
                     order[tail].y2=getchar()-'';

                     tail++;
                     break;
                 }
                 case 'a':{
                     order[tail].x=x;
                     order[tail].y=y;

                     order[tail].avg=;

                     order[tail].x1=getchar();
                     while(order[tail].x1<'A'||order[tail].x1>'Z') order[tail].x1=getchar();
                     order[tail].x1-='A';
                     order[tail].y1=getchar()-'';

                     order[tail].x2=getchar();
                     while(order[tail].x2<'A'||order[tail].x2>'Z') order[tail].x2=getchar();
                     order[tail].x2-='A';
                     order[tail].y2=getchar()-'';

                     tail++;
                     break;
                 }
                 default:{
                     flag=;
                     break;
                 }
             }
         }while(flag&&i++<=);

         for(int i=;i<tail;i++)
         {
             int tsa=;
             for(int tx=order[i].x1;tx<=order[i].x2;tx++)
             for(int ty=order[i].y1;ty<=order[i].y2;ty++)
                 tsa+=array[tx][ty];
             if(order[i].avg) tsa/=(order[i].x2-order[i].x1+)*(order[i].y2-order[i].y1+);
             array[order[i].x][order[i].y]=tsa;
         }
     }
     return ;
 }

T3

T4 GMOJ1574. X-因子链

(File IO): input:factor.in output:factor.out

时间限制: 1000 ms  空间限制: 131072 KB  具体限制

Goto ProblemSet

题目描述

　　给一个正整数X，一个长度为m的X-因子链是指这样一个序列：X0=1，X1，X2，。。。，Xm=X满足：Xi<Xi+1同时Xi|Xi+1(Xi+1能被Xi整除)

　　要求X-因子链的最大长度Len和长度为Len的X-因子链的数量。

输出

　　一行，两个整数，分别表示最大长度和该长度链的种数。

样例输入

　　100

样例输出

　　4 6

数据范围限制

（空）

Solution

稍作思考即可

P1问题转化

有一个数列，已知首项（为1）与尾项，每一项都是前一项的整数倍，且每一项都大于前一项。

如何使此数列最长？

设相邻两项的商为k

那么k一定是越小越好

但是所有k之积必须等于尾项

那么，k即为尾项的所有质因数。

所以第一问只需求x的质因数个数。

P1Code

int maxlen=0x3f3f3f3f,kind,x;
int lian[];
IL int prime_factor(int num)
{
    int ans=;
    if(num==) return ;
    if(num==) return ;
    int i=;
    while(num!=)
    {
        while(num%i==)
        {
            num/=i;
            ans++;
            lian[i]++;
        }
        i++;
    }
    return ans;
}

（使用IL（inline）加速调用）

填写lian[i]++是为了第二问的

P2看穿此题

排列组合类型题

因子链的数量，即这些prime factors可以排成多少种

以样例中的100为例

100=2*2*5*5=2²*5²

那么这串链有两种、四个元素

不去重的话，一共有4!种排列

但是这道题是要问的是种类（即去重的）数量……

现在只观察其中的两个2

2*2*？*？

这时两个2如果交换，会被算入全排列的数量中，但是不能被算入种类数量中！

两个2可以有两种摆放位置的顺序

那么4!=24除去两次2（两个2和两个5的）即可。

若有三个2呢？

三个2可以有3!=3*2*1=6种摆放位置的顺序

把n!除以6即可。

P2数学推导

设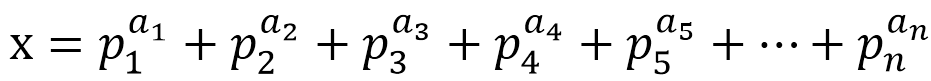

其中ans为质因数的数量

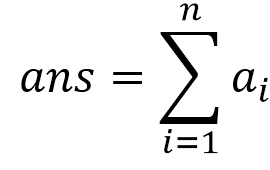
所以

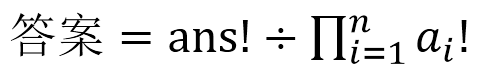
P2Code

若数据较小（不存在的），可使用dfs暴力枚举

 IL void dfs(int depth)
 {
     if(depth==maxlen){
         kind++;
         return;
     }
     for(int i=;i<=x;i++)
     {
         if(lian[i]>){
             lian[i]--;
             dfs(depth+);
             lian[i]++;
         }
     }
 }

dfs暴力枚举

于是20分……枉费了我辛辛苦苦思考呀！

阶乘运算

 IL long long factor(int num)
 {
     if(num==) return ;
     long long ans=;
     for(int i=;i<=num;i++)
         ans*=i;
     return ans;
 }

factor

如果只是按照普通的阶乘的话，比较容易爆long long

解决方案有两种：

1、预处理（或者打表、记忆化……）出1~20的阶乘（极限应该是31！，但会超过unsigned long long，且数据也没有那么大哈哈），factor函数可用递归。

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<map>
 #include<set>
 #include<vector>
 #include<algorithm>
 #define IL inline
 using namespace std;
 int lian[];
 unsigned long long kind,maxlen=0x3f3f,x;
 unsigned long long fact[]={,,,,,,,,,,,,,,,,,,,,};
 IL unsigned long long factor(int num)
 {
     if(fact[num]!=) return fact[num];
     return fact[num]=factor(num-)*num;
 }

递归加打表

如果记忆化的话，其实就可以不用打表了（反正都是2、3毫秒的样子）。

2、把一个数的阶乘分解成

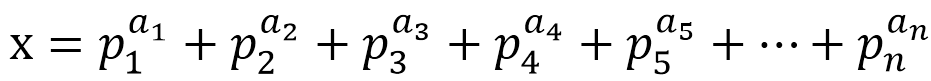
这样子

用结构体数组储存。

最后要相除则换成相减即可

——来自某某不让我去B组的老师的想法

Code

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<map>
 #include<set>
 #include<vector>
 #include<algorithm>
 #define IL inline
 using namespace std;
 int lian[];
 unsigned long long kind,maxlen=0x3f3f,x;
 unsigned long long fact[]={,,,,,,,,,,,,,,,,,,,,};
 IL int prime_factor(int num)
 {
     int ans=;
     if(num==) return ;
     if(num==) return ;
     int i=;
     while(num!=)
     {
         while(num%i==)
         {
             num/=i;
             ans++;
             lian[i]++;
         }
         i++;
     }
     return ans;
 }
 IL unsigned long long factor(int num)
 {
     if(fact[num]!=) return fact[num];
     return fact[num]=factor(num-)*num;
 }
 int main()
 {
 //    freopen("factor.in","r",stdin);
 //    freopen("factor.out","w",stdout);
     scanf("%lld",&x);
     maxlen=prime_factor(x);
     printf("%lld ",maxlen);
     kind=factor(maxlen);
     for(unsigned long long i=;i<=sqrt(x);i++)
     if(lian[i]>)
         kind/=factor(lian[i]);
     printf("%lld",kind);
     return ;
 }

这道题的代码在尝试着极限……0ms，512KB！

可是……真的有0ms……