[板子]快速幂&矩阵快速幂

不会的来这看：https://www.cnblogs.com/CXCXCXC/p/4641812.html

简单的一说：当转换为二进制的时候有位运算这种黑科技，&相当于%2判断奇偶性。

x&1==0为偶，x&1==1为奇

&运算通常用于二进制取位操作，例如一个数 & 1 的结果就是取二进制的最末位。还可以判断奇偶x&1==0为偶，x&1==1为奇

只有在奇数情况的时候把base乘进去，每一次用base*base扩大平方，b的二进制去除一位。

 int poww(int a,int b){
     int ans=,base=a;
     while(b!=){
         if(b&==)
         　　ans*=base;
         base*=base;
         b>>=;
 　 }
     return ans;
 }

接下来是矩阵快速幂。

摘自：blog.csdn.net/wust_zzwh/article/details/52058209

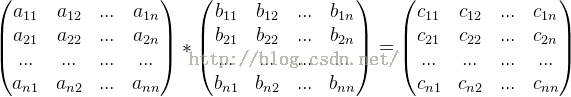
其中c[i][j]为A的第i行与B的第j列对应乘积的和，即:

 #include<bits/stdc++.h>

 #define LL long long
 using namespace std;

 LL n,k;

 const long long pi=1e9+;

 struct ska{
     LL a[+][+];
 }p,pp;

 ska X(ska x,ska y){
     ska box;

     for(LL i=;i<=n;i++){
         for(LL j=;j<=n;j++){
             box.a[i][j]=;
         }
     }

     for(LL i=;i<=n;i++){

         for(LL j=;j<=n;j++){

             for(LL k=;k<=n;k++){

                 box.a[i][j]=(box.a[i][j]+(x.a[i][k]*y.a[k][j])%pi)%pi;

             }
         }
     }

     return box;
 }

 ska quick_pow(LL kk){

     ska ans;

     for(LL i=;i<=n;i++){
         ans.a[i][i]=;
     }

     while(kk!=){

         if(kk&==){

             ans=X(ans,p);
         }

         kk>>=;

         p=X(p,p);

     }

     return ans;
 }

 int main(){
     scanf("%lld%lld",&n,&k);

     for(LL i=;i<=n;i++){

         for(LL j=;j<=n;j++){

             scanf("%lld",&p.a[i][j]);

         }
     }

     pp=quick_pow(k);

     for(LL i=;i<=n;i++){

         for(LL j=;j<=n;j++){

             printf("%lld ",pp.a[i][j]);

         }

         cout<<endl;
     }
     return ;
 }