Https个人总结
花了一个星期终于搞懂了..
HTTPS个人总结:
一、RSA算法

公钥:可以分发给任意的钥匙
私钥:自己保留起来,不分发给别人的钥匙
RSA算法:
- 找出质数p、q
- n = p*q
- Φ(n)=(p-1)*(q-1)
- 公钥e 要求 1<e<Φ(n) 并且e和Φ(n)互质
- 私钥d 要求e*d除以Φ(n)余数为1
- 密文C:m^e 除以 n 求余数C
- 明文m:c^d 除以n 求余数m
举例:
- 找出质数p,q:p、q: 3 17
- n = p*q: 51
- Φ(n)=(p-1)*(q-1) =2*16 =32
- 公钥e 要求 1<e<Φ(n) 并且e和Φ(n)互质 取11
- 私钥d: 要求e*d除以Φ(n)余数为1 即:11*d/32 …, 1 d取3
明文m取5
- 密文c,m^e 除以 n 求余数C:5^11/51 … 11
- 明文m,c^d 除以n 求余数m:11^3/51 … 5
二、加密过程: (公钥e加密 私钥d解密)
A---->B 假设A要把消息m传给B
1.首先B要自己确定pq生成n、Φ(n)、e、d
2.B把e(公钥) n(大数)传播给A,
3.消息m用e和n加密 就可以得到c,所以两个人之间通信传播的是: n e c
B有私钥d 所以只有B可以解密。
三、数字签名:
A<----B 假设B要把消息m传给A,他想附上签名
- 对消息进行哈希计算(一般不直接对消息进行签名,而是对消息哈希值进行签名)
- 用私钥对哈希值进行加密,生成签名
- 将签名附加再消息后面,一起发送过去
这个过程也涉及了RSA
B首先生成了 n Φ(n) 公钥e 私钥d
B将消息m用 d 加密生成签名s
然后将公钥传播给网络间任意的人。
根据RSA算法原理… e和d其实是对称的,知道哪一个都可以求出另一个,
现在所有人都可以解密,
假设B把 明文m 公钥e和签名s 给了A
A可以用公钥e来解密S ,得到m的哈希值
然后自己再给m进行哈希,发现两个哈希值一样,因为只有B有私钥,只有B才能进行签名(用私钥加密) 所以证明了消息m是B签名的
四、证书:
证书实际上是对公钥进行数字签名,对公钥合法性提供证明的技术。
窝们对签名进行验证时,需要用到公钥,如果公钥是伪造的,那怎么办?
这时候证书就派上用场了
证书一般包含:
*公钥(证书中是带有公钥的)
*公钥的数字签名
*公钥拥有者的信息
若证书验证成功,这表示公钥是合法,可信的。
认证机构(Certification Authority,CA)
CA就是能够认定”公钥确实属于此人,并能生成公钥数字签名的组织或机构
生成证书:
服务器将公钥A给CA(公钥是服务器的)”
CA用自己的私钥B给公钥A加密,生成数字签名A
CA把公钥A,数字签名A,附加一些服务器信息整合在一起,生成证书,发回给服务器。
然后服务器将公钥,签名和证书发给客户端,
验证证书:
客户端得到证书
客户端得到证书的公钥B(通过向CA请求)
客户端用公钥对数字签名解密得到哈希值
客户端对公钥进行哈希值计算
两个哈希值对比,如果相同,证明证书合法,服务器的公钥也是可信的。
证书作废,当服务器私钥丢失,被盗时,认证机构需要对证书进行作废(revoke)
要作废证书,认证机构需要制作一张证书作废清单(Certificate Revocation List) 简称CRL
假设有Bob的证书,证书有合法的认证机构签名,而且再有效期内,但仅凭这些还不能说明证书一定有效,还需要查询认证机构最新CRL,并确认该证书是否有效。
五、HTTPS:
SSL 协议既用到了公钥加密技术又用到了对称加密技术。
资料1:
① 客户端的浏览器向服务器传送客户端SSL 协议的版本号,加密算法的种类,产生的随机数,以及其他服务器和客户端之间通讯所需要的各种信息。
② 服务器向客户端传送SSL 协议的版本号,加密算法的种类,随机数以及其他相关信息,同时服务器还将向客户端传送自己的证书。
③ 客户利用服务器传过来的信息验证服务器的合法性,服务器的合法性包括:证书是否过期,发行服务器证书的CA 是否可靠,发行者证书的公钥能否正确解开服务器证书的“发行者的数字签名”,服务器证书上的域名是否和服务器的实际域名相匹配。如果合法性验证没有通过,通讯将断开;如果合法性验证通过,将继续进行第四步。
④ 用户端随机产生一个用于后面通讯的“对称密码”,然后用服务器的公钥(服务器的公钥从步骤②中的服务器的证书中获得)对其加密,然后将加密后的“预主密码”传给服务器。
⑤ 如果服务器要求客户的身份认证(在握手过程中为可选),用户可以建立一个随机数然后对其进行数据签名,将这个含有签名的随机数和客户自己的证书以及加密过的“预主密码”一起传给服务器。
⑥ 如果服务器要求客户的身份认证,服务器必须检验客户证书和签名随机数的合法性,具体的合法性验证过程包括:客户的证书使用日期是否有效,为客户提供证书的CA 是否可靠,发行CA 的公钥能否正确解开客户证书的发行CA 的数字签名,检查客户的证书是否在证书废止列表(CRL)中。检验如果没有通过,通讯立刻中断;如果验证通过,服务器将用自己的私钥解开加密的“预主密码”,然后执行一系列步骤来产生主通讯密码(客户端也将通过同样的方法产生相同的主通讯密码)。
⑦ 服务器和客户端用相同的主密码即“通话密码”,一个对称密钥用于SSL 协议的安全数据通讯的加解密通讯。同时在SSL 通讯过程中还要完成数据通讯的完整性,防止数据通讯中的任何变化。
⑧ 客户端向服务器端发出信息,指明后面的数据通讯将使用的步骤⑦中的主密码为对称密钥,同时通知服务器客户端的握手过程结束。
⑨ 服务器向客户端发出信息,指明后面的数据通讯将使用的步骤⑦中的主密码为对称密钥,同时通知客户端服务器端的握手过程结束。
⑩ SSL 的握手部分结束,SSL 安全通道的数据通讯开始,客户和服务器开始使用相同的对称密钥进行数据通讯,同时进行通讯完整性的检验。
资料2:
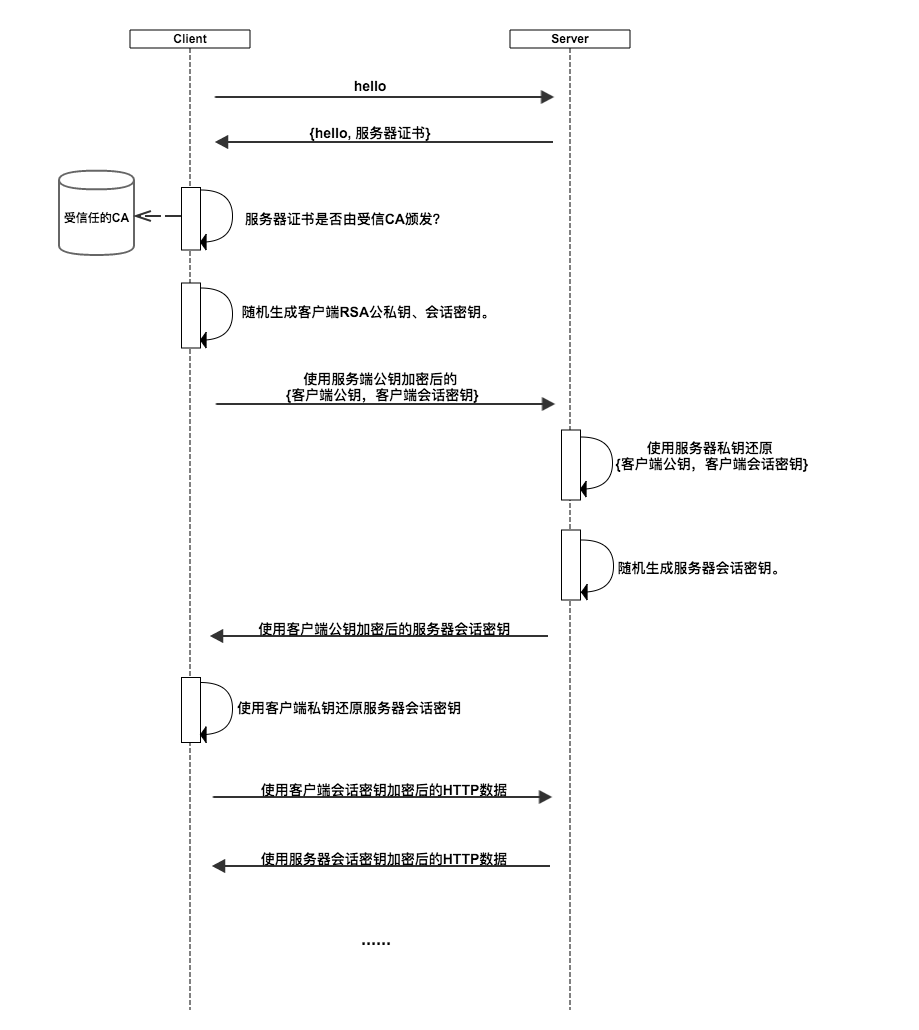
资料1和资料2的区别是资料2中使用了不同的对称密钥, 资料1使用了相同的对称密钥,可能这个差别是在协商的过程中产生的。
资料3:
众所周知,WEB服务存在http和https两种通信方式,http默认采用80作为通讯端口,对于传输采用不加密的方式,https默认采用443,对于传输的数据进行加密传输
目前主流的网站基本上开始默认采用HTTPS作为通信方式,一切的考虑都基于对安全的要求,那么如何对自己的网站配置HTTPS通信,是本文着重介绍的
本文的主要内容包括:https加密传输的原理、如何申请https所用的CA证书,如何配置WEB服务支持https
1、https原理通俗讲解
https=http+ssl,顾名思义,https是在http的基础上加上了SSL保护壳,信息的加密过程就是在SSL中完成的
首先我们先不谈https,先从一个简单的通讯原理图讲起:

客户端发送一句client hello给服务器端,服务器端返回一句serverhello给客户端,鉴于本文讨论是https的加密主题,我们只讨论信息传输的加密问题
实现客户端和服务端发送的信息client hello 和server hello,即使中间的包被窃取了,也无法解密传输的内容
http:client hello和server hello在通讯的过程中,以明文的形式进行传输,采用wireshark抓包的效果如下图:

有没有感觉这个的信息传输是完全暴露在互联网上面,你请求的所有信息都可以被窥测到,是不是感觉心一凉,不过不用担心,我们的安全信息现在都是采用https的传输,后面讲到https的时候大家心里会顿时轻松。但这不是最关键的,http的传输最大的隐患是信息劫持和篡改,如下图:

可以看到,http的信息传输中,信息很容易被×××给劫持,更有甚者,×××可以伪装服务器将篡改后的信息返回给用户,试想一下,如果×××劫持的是你的银行信息,是不是很可怕。所以对于http传出存在的问题可以总结如下:
(1)信息篡改:修改通信的内容
(2)信息劫持:拦截到信息通信的内容
这些是http不安全的体现,说完http,我们回到本文的主题https,看下人家是怎么保护信息的,所有的请求信息都采用了TLS加密,如果没有秘钥是无法解析传输的是什么信息
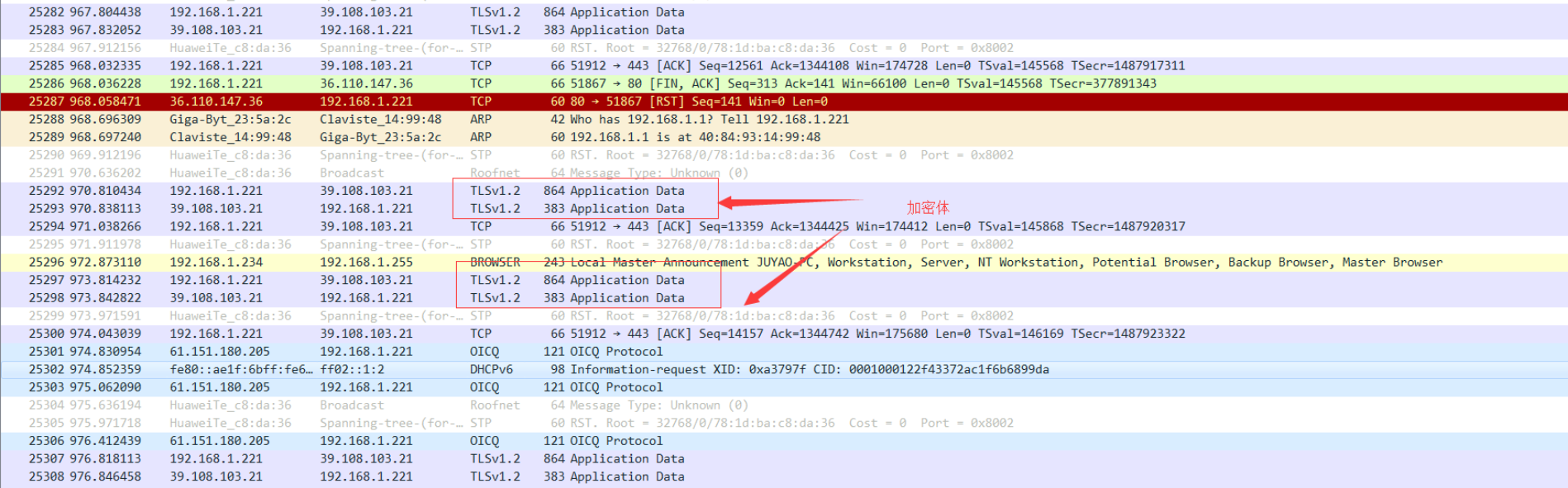
对于加密传输存在对称加密和非对称加密
对称加密

对称加密传输
当客户端发送Hello字符串的时候,在进行信息传输前,采用加密算法(上图中的秘钥S)将hello加密程JDuEW8&*21!@#进行传输,即使中间被×××劫持了,如果没有对应的秘钥S也无法知道传出的信息为何物,在上图中信息的加密和解密都是通过同一个秘钥进行的,对于这种加密我们称之为对称加密,只要A和B之间知道加解密的秘钥,任何第三方都无法获取秘钥S,则在一定条件下,基本上解决了信息通信的安全问题。但在现实的情况下(www),实际的通讯模型远比上图复杂,下图为实际的通信模型
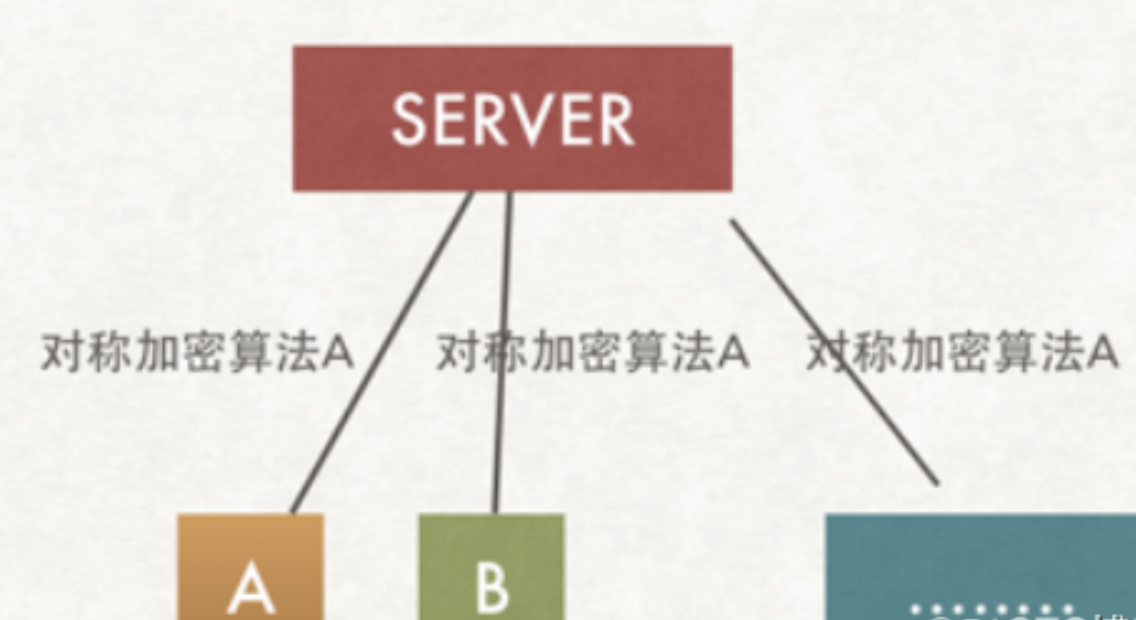
server和所有的client都采用同一个秘钥S进行加解密,但大家思考下,如果这样的话,无异于没有加密,请做下思考
由于server和所有的client都采用同一个秘钥S,则×××们作为一个client也可以获取到秘钥S,此地无银三百两。所以在实际的通讯中,一般不会采用同一个秘钥,而是采用不同的秘钥加解密,如下图
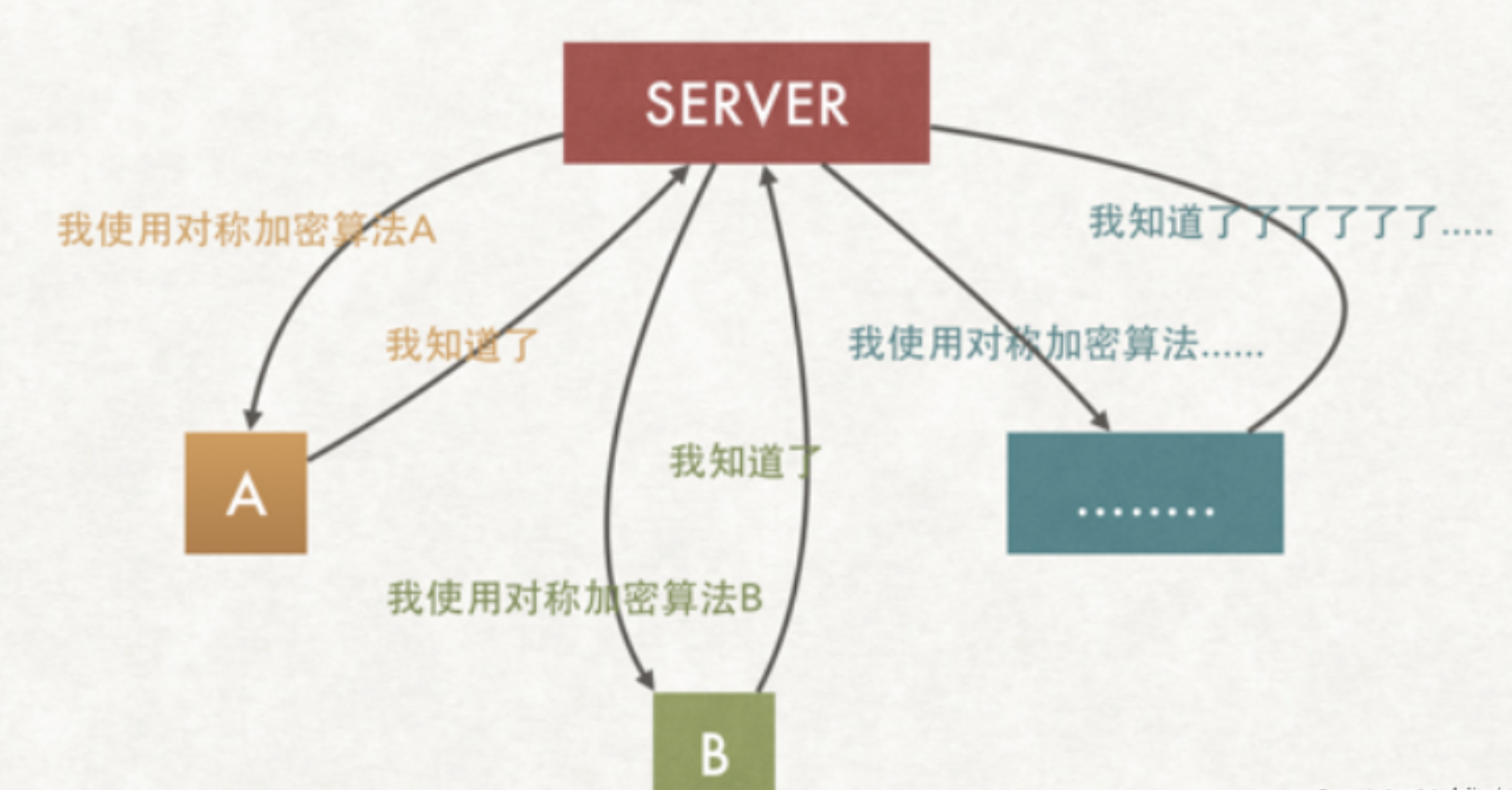
通过协商的方式获取不同的秘钥
如上图,A和server通信采用对称加密A算法,B和server通信采用对称秘钥B算法,因此可以很好的解决了不同的客户端采用相同的秘钥进行通讯的问题
那现在又存在问题了,A通过明文传输和server协商采用了加密算法A,但这条信息本身是没有加密的,因此×××们还是可以窃取到秘钥的,整个的通讯仍然存在风险。那该如何处理呢?有人说,把这条信息(协调秘钥的过程)再次加密,那是不是还要协商加密秘钥,如此反复,永无止境。从根本上无法解决信息通讯的安全问题
如何对协商过程进行加密
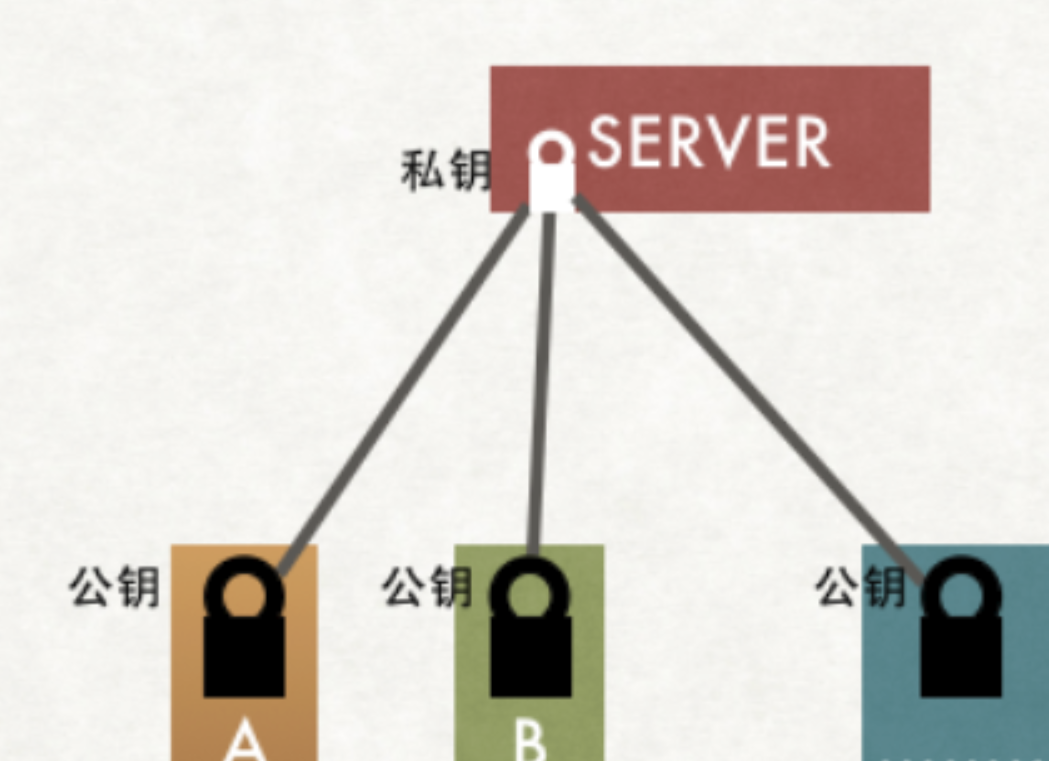
非对称加密原理图
在密码学跟对称加密一起出现的,应用最广的加密机制“非对称加密”,如上图,特点是私钥加密后的密文,只要是公钥,都可以解密,但是反过来公钥加密后的密文,只有私钥可以解密。私钥只有一个人有,而公钥可以发给所有的人。
基于上述的特点,我们可以得出如下结论:
(1)公钥是开放给所有人的,但私钥是需要保密的,存在于服务端
(2)服务器端server向client端(A、B.....)的信息传输是不安全的:因为所有人都可以获取公钥
(3)但client端(A、B.....)向server端的信息传输确实安全的:因为私钥只有server端存在
因此,如何协商加密算法的问题,我们解决了,非对称加密算法进行对称加密算法协商过程。
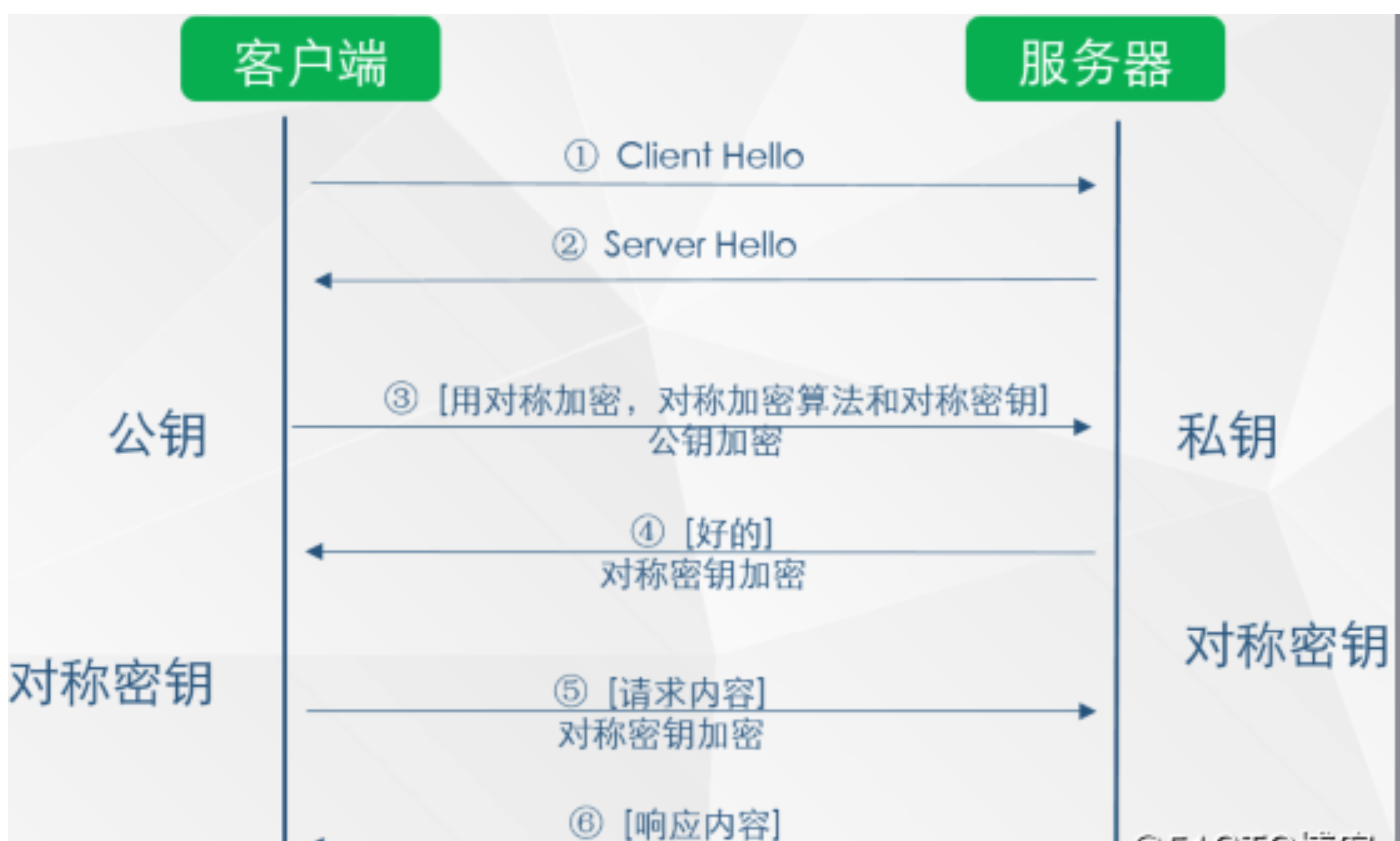
在这里我们做个小结:
信息通信采用http是不安全的,存在信息劫持、篡改的风险,https是加密传输,是安全的通信,对于https加密的过程,我们首先介绍的对称加密,采用对称加密进行通信存在秘钥协商过程的不安全性,因此我们采用了非对称加密算法解决了对协商过程的加密,因此https是集对称加密和非对称加密为一体的加密过程
安全的获取公钥
细心的人可能已经注意到了如果使用非对称加密算法,我们的客户端A,B需要一开始就持有公钥,要不没法开展加密行为啊。
这下,我们又遇到新问题了,如何让A、B客户端安全地得到公钥?
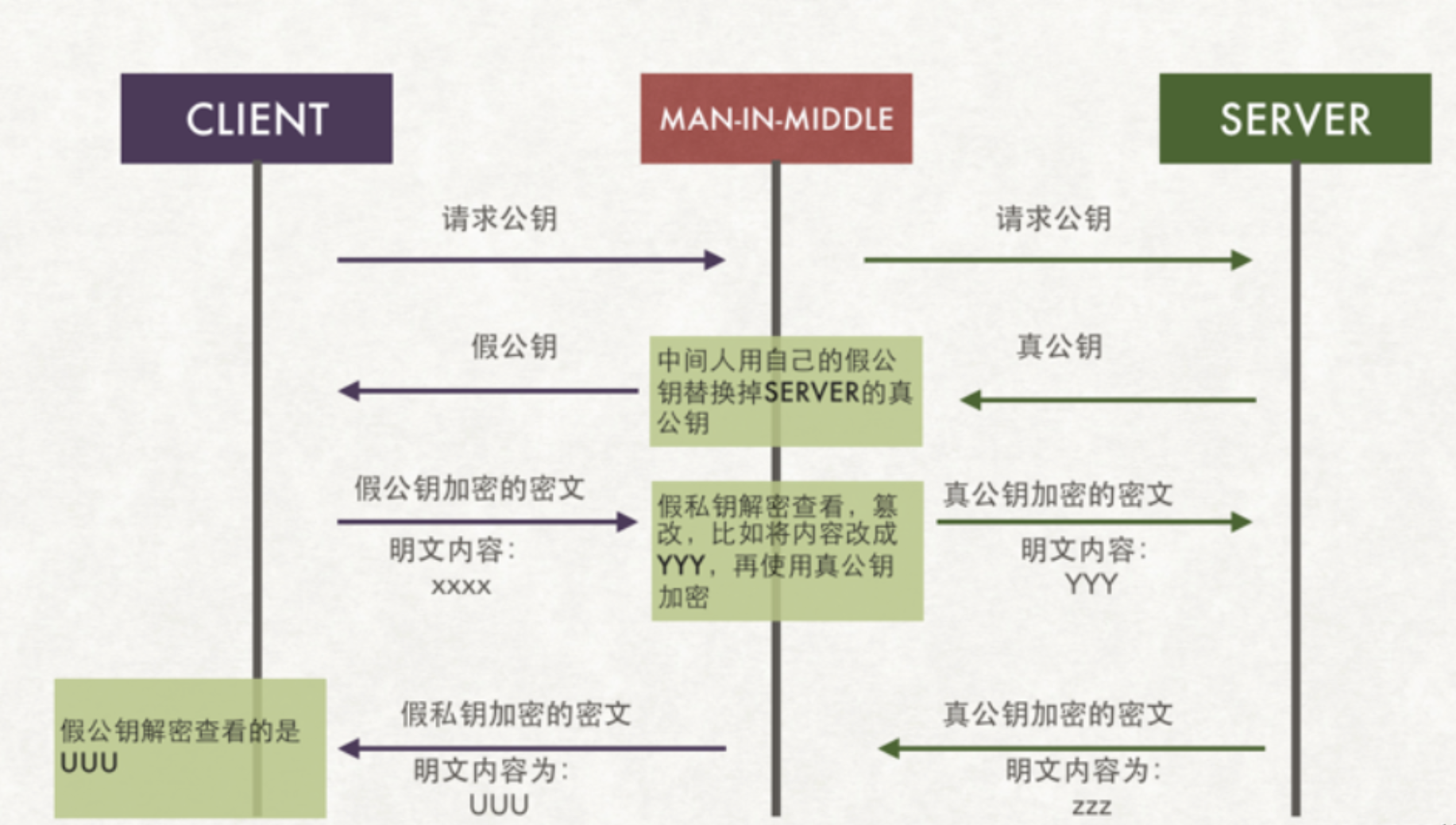
client获取公钥最最直接的方法是服务器端server将公钥发送给每一个client用户,但这个时候就出现了公钥被劫持的问题,如上图,client请求公钥,在请求返回的过程中被×××劫持,那么我们将采用劫持后的假秘钥进行通信,则后续的通讯过程都是采用假秘钥进行,数据库的风险仍然存在。在获取公钥的过程中,我们又引出了一个新的话题:如何安全的获取公钥,并确保公钥的获取是安全的, 那就需要用到终极武器了:SSL 证书(需要购买)和CA机构
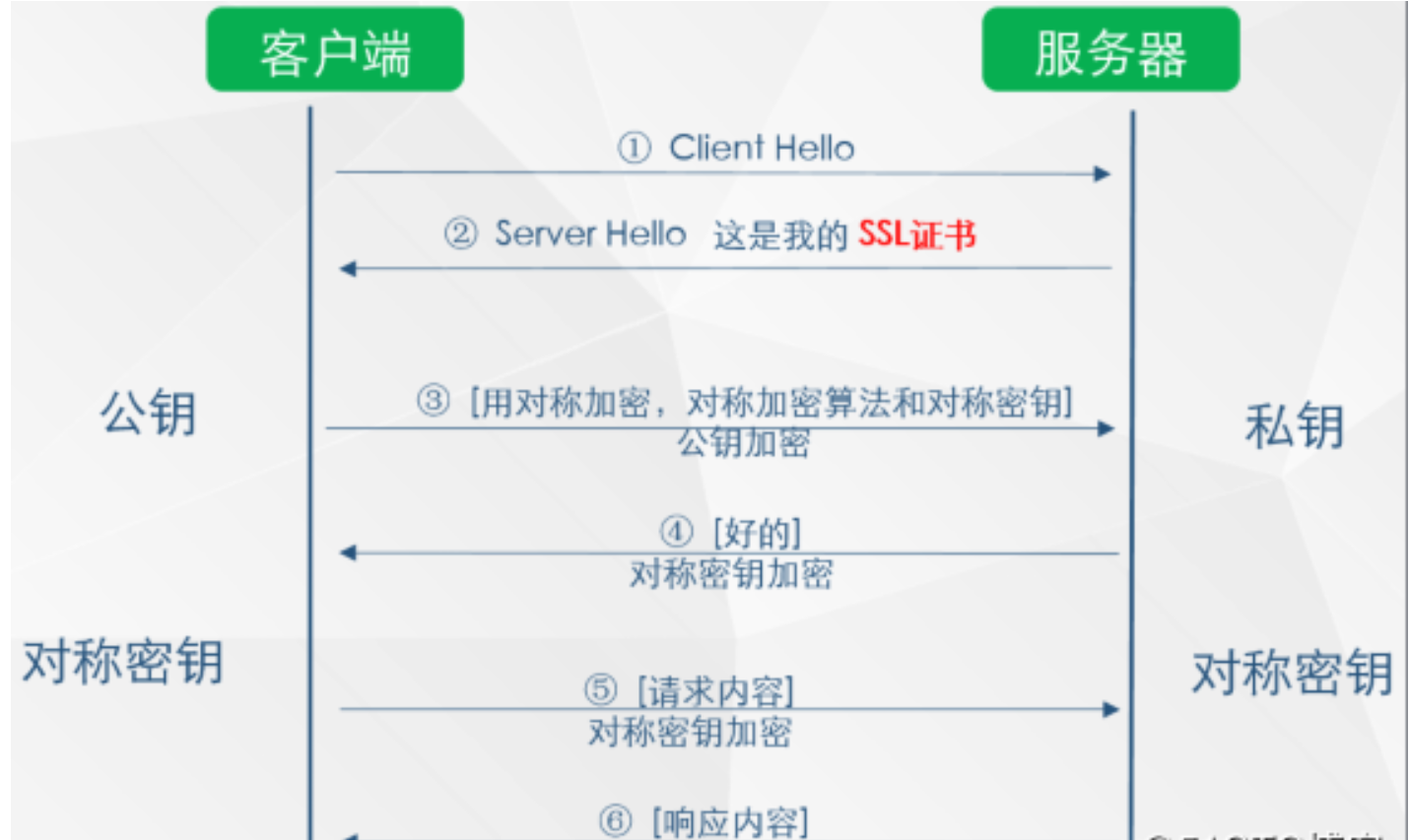
如上图所示,在第 ② 步时服务器发送了一个SSL证书给客户端,SSL 证书中包含的具体内容有证书的颁发机构、有效期、公钥、证书持有者、签名,通过第三方的校验保证了身份的合法,解决了公钥获取的安全性
以浏览器为例说明如下整个的校验过程:
(1)首先浏览器读取证书中的证书所有者、有效期等信息进行一一校验
(2)浏览器开始查找操作系统中已内置的受信任的证书发布机构CA,与服务器发来的证书中的颁发者CA比对,用于校验证书是否为合法机构颁发
(3)如果找不到,浏览器就会报错,说明服务器发来的证书是不可信任的。
(4)如果找到,那么浏览器就会从操作系统中取出 颁发者CA 的公钥,然后对服务器发来的证书里面的签名进行解密
(5)浏览器使用相同的hash算法计算出服务器发来的证书的hash值,将这个计算的hash值与证书中签名做对比
(6)对比结果一致,则证明服务器发来的证书合法,没有被冒充
(7)此时浏览器就可以读取证书中的公钥,用于后续加密了
至此第一部分关于HTTPS的原理介绍已经结束了,总结一下:
HTTPS要使客户端与服务器端的通信过程得到安全保证,必须使用的对称加密算法,但是协商对称加密算法的过程,需要使用非对称加密算法来保证安全,然而直接使用非对称加密的过程本身也不安全,会有中间人篡改公钥的可能性,所以客户端与服务器不直接使用公钥,而是使用数字证书签发机构颁发的证书来保证非对称加密过程本身的安全。这样通过这些机制协商出一个对称加密算法,就此双方使用该算法进行加密解密。从而解决了客户端与服务器端之间的通信安全问题。
Https个人总结的更多相关文章
- 【流量劫持】躲避 HSTS 的 HTTPS 劫持
前言 HSTS 的出现,对 HTTPS 劫持带来莫大的挑战. 不过,HSTS 也不是万能的,它只能解决 SSLStrip 这类劫持方式.但仔细想想,SSLStrip 这种算劫持吗? 劫持 vs 钓鱼 ...
- HTTPS 互联网世界的安全基础
近一年公司在努力推进全站的 HTTPS 化,作为负责应用系统的我们,在配合这个趋势的过程中,顺便也就想去搞清楚 HTTP 后面的这个 S 到底是个什么含义?有什么作用?带来了哪些影响?毕竟以前也就只是 ...
- 7.让网站支持http和https的访问方式
平台之大势何人能挡? 带着你的Net飞奔吧!:http://www.cnblogs.com/dunitian/p/4822808.html#iis 怎么让网站在本地支持SSL?http://www.c ...
- HTTPS简介
一.简单总结 1.HTTPS概念总结 HTTPS 就是对HTTP进行了TLS或SSL加密. 应用层的HTTP协议通过传输层的TCP协议来传输,HTTPS 在 HTTP和 TCP中间加了一层TLS/SS ...
- 猖獗的假新闻:2017年1月1日起iOS的APP必须使用HTTPS
一.假新闻如此猖獗 刚才一位老同事 打电话问:我们公司还是用的HTTP,马上就到2017年了,提交AppStore会被拒绝,怎么办? 公司里已经有很多人问过这个问题,回答一下: HTTP还是可以正常提 ...
- WebAPi之SelfHost自创建证书启动Https疑难解惑及无法正确返回结果
前言 话说又来需求了,之前对于在SelfHost中需要嵌套页面并操作为非正常需求,这回来正常需求了,客户端现在加了https,老大过来说WebAPi访问不了了,这是什么情况,我去试了试,还真是这个情况 ...
- 苹果强制使用HTTPS传输了怎么办?——关于HTTPS,APP开发者必须知道的事
WeTest 导读 2017年1月1日起,苹果公司将强制使用HTTPS协议传输.本文通过对HTTPS基础原理和通信过程内容的讲解,介绍APP开发者在这个背景下的应对办法. 几周前,我们在<htt ...
- 【原创】免费申请SSL证书【用于HTTPS,即是把网站从HTTP改为HTTPS,加密传输数据,保护敏感数据】
今天公司有个网站需要改用https访问,所以就用到SSL证书.由于沃通(以前我是在这里申请的)暂停了免费的SSL证书之后,其网站推荐了新的一个网站来申请证书,所以,今天因为刚好又要申请一个证书,所以, ...
- https 安全验证问题
最近为了满足苹果的 https 要求, 经过努力终于写出了方法 验证 SSL 证书是否满足 ATS 要求 nscurl --ats-diagnostics --verbose https://你的域名 ...
- Ubuntu下配置apache开启https
一.HTTPS简述随着网络的日常,信息安全越来越重要,传统的网站都是http协议明文传输,而HTTPS协议是由SSL+HTTP协议构建的可进行加密传输.身份认证的网络协议,比http协议安全. 那ht ...
随机推荐
- (八)统一配置中心-Config
对于配置的重要性,我想我不用进行任何强调,大家都可以明白其重要性.在普通单体应用,我们常使用配置文件(application(*).properties(yml))管理应用的所有配置.这些配置文件在单 ...
- vue 父子组件传值以及方法调用,平行组件之间传值以及方法调用大全
vue项目经常需要组件间的传值以及方法调用,具体场景就不说了,都知道.基本上所有的传值都可以用vuex状态管理来实现,只要在组件内监听vuex就好. vue常用的传值方式以及方法有: 1. 父值传子( ...
- SVN 部分常用命令
1. svn status 提交前显示出本地文本和版本库文本的区别 [url=] L abc.c # svn已经在.svn目录锁定了abc.c M bar.c # bar.c的内容已经在本地修改过了 ...
- C# HttpHelper万能框架实现 接口
POST请请求是使用Http协议与请求的URL进行连接,然后再写入数据,最后关闭连接的过程 方法(1) //要Post的数据 string postdate = "a=123&c=4 ...
- plsql 查询历史执行语句
control+e. 如果执行删除.修改.增加的操作,未提交的历史记录中也有.
- servlet中Cookie的编码问题
a.什么是Cookie的编码问题? Cookie只能存放合法的ascii字符,如果是非asicc字符(比如中文), 需要转换成合法的ascii字符的形式. b.如何处理? ...
- NodeJS学习笔记 (6)网络服务-http-res(ok)
原文:https://github.com/chyingp/nodejs-learning-guide 自己敲代码: 概览 http模块四剑客之一的res,应该都不陌生了.一个web服务程序,接受到来 ...
- vue+element-ui+slot-scope或原生实现可编辑表格(日历)
你们公司的产品是不是还在做一个可编辑表格功能? 1.前言 咱开发拿到需求大多数是去网上找成型的组件,找不到再看原生的方法能否实现,大牛除外哈,大牛一般喜欢封装组件框架. 2.思路 可编辑表格在后台管理 ...
- exadata(硬件更换文档部分)
Maintaining Flash Disks Replacing a Flash Disk Due to Flash Disk Failure Each Exadata Storage Server ...
- 在独立的文件里定义WPF资源
一.文章概述 本演示介绍怎样在单独的文件里定义WPF资源.并在须要的地方调用相关资源文件. 相关下载(代码.屏幕录像):http://pan.baidu.com/s/1sjO7StB 在线播放:htt ...
