Coding the Matrix (1)：向量

1. list 画点

>>> from plotting import plot
>>> L = [[2, 2], [3, 2], [1.75, 1], [2, 1], [2.25, 1], [2.5, 1], [2.75, 1], [3, 1], [3.25, 1]]
>>> plot(L)

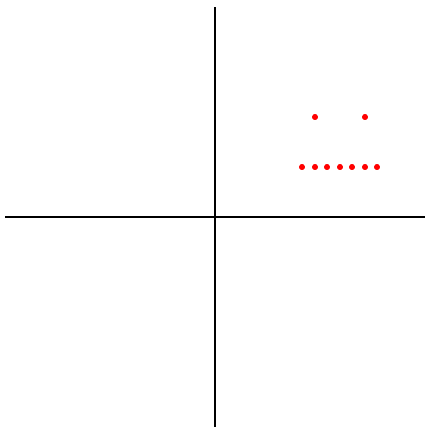
2. 缩放

alpha × vec = [alpha × elem for elem in vec]

>>> def scalar_vector_mult(alpha, v): return [alpha*x for x in v]
...
>>> v = [3, 2]
>>> plot([scalar_vector_mult(i/10., v) for i in range(11)], 5)

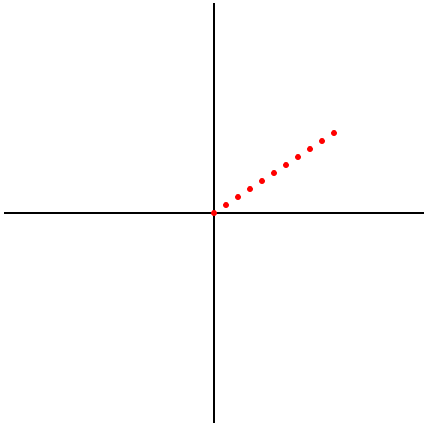
3. 仿射：加乘组合

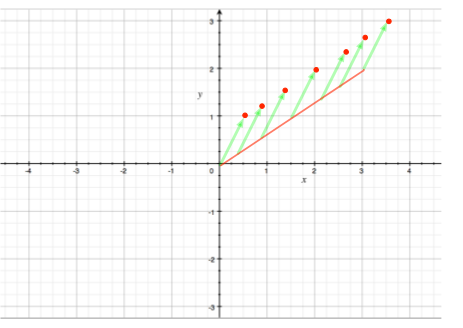
得到从 [0, 0] + [0.5,1] 开始到 [3, 2] + [0.5, 1] 结束的线段。 这种表示方法对 端点来说不具有对称性。如何转换？

现在对于端点来说就具有对称性了。通过这两个端点的直线包含了两个端点对应向量的 仿射集合。

4. GF(2) 加密

a) 要将期中考试的一份试卷交给两个助教，为了防止某一个助教舞弊，发给两个人的加密后的数据必须 合二为一才能进行解密，具体过程如下：

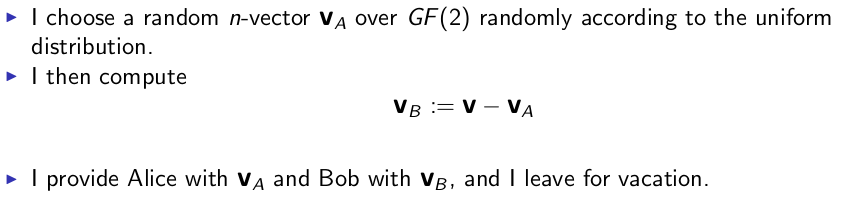
b) 电脑认证登陆——黑客可能窃听，不适合直接传输用户密码。解决方案：电脑给出一串二进制问题，用户掌握一串二进制密码，在 GF(2) 上点乘（先乘再加），得到输出。

黑客窃听到数个电脑的问题 alpha 和用户计算后的结果 beta，需要知道用户的密码，需要解方程：

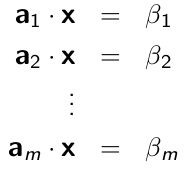
5. 点乘

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为:

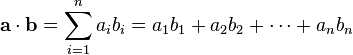
在欧几里得空间中，点积可以直观理解为：

用公式可以表示为：

直观地说，就是向量 A 在向量 B 方向的投影，再乘以 B 的长度。如果将 B 的长度标准化，那么点乘就可以表示两个向量之间的相似性了。比如在一段长音频中匹配一段短音频，可以把短的音频逐个往后移动，每次移动进行一次点乘计算，值越大，相似性越大，DFT 和 DCT 变换都是基于这种操作求不同频域的组分大小的。

编程待续：点乘——用字典类型编写向量类

                             用向量类解三角线性方程组的根