简述
AC 自动机是什么
AC 自动机有什么用
AC 自动机·初探
AC 自动机·原理分析
AC 自动机·代码实现
AC 自动机·更进一步
从 AC 自动机到 fail 树
- 例题一
- 例题二
结语

简述

我竟然会了如此高深的算法的皮毛

\(Update\ on\ 2020.4.10\)：看了其他 dalao 的文章后发现被 diss 了，于是重修了本文。

根据众多神犇的 blog 所说，学习 AC 自动机前要学习两个东西：

trie 树。（可以康康我的 blog trie 树学习笔记）
KMP。（同样可以康康我的 blog KMP 学习笔记）

既然我们都已经会了以上两个数据结构/算法，为什么不进一步学习呢？

现在开始进入正题。

AC 自动机是什么

形式上，AC 自动机基于由若干模式串构成的 Trie 树，并在此之上增加了一些 fail 边。

本质上，AC 自动机是一个关于若干模式串的 DFA（确定有限状态自动机），

并且接受且仅接受以某一个模式串作为后缀的字符串。

——ouuan 神犇

有了 AC 自动机，我们把一个文本串逐位地输入到自动机中，当匹配时就会处于接受状态。

P.S. 以上内容转载自ouuan 神犇的文章。

AC 自动机有什么用

我认为学习一个算法的前提是了解它的作用，所以我们要知道 AC 自动机使用来干什么的。

一定要记住：很多人听到这个名字后很兴奋，但这不是一个可以自动帮你 AC 题目的算法。

那么为什么叫 AC 自动机呢，以下来自某度某科：

Aho-Corasick automation，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法。

好的，这是一个多模匹配算法，那么什么是多模匹配呢？

首先我们知道 KMP 是一种高效的单模匹配算法，就是说从一个文本串中找到一个模式串的所在位置。

那么 AC 自动机就是用来求解：从一个文本串中找到多个模式串的所在位置。

当然，最直接的方法是暴力或者多次KMP，但是复杂度无疑都会爆炸，所以就有了这个高效的多模匹配算法。

AC 自动机·初探

首先，我们要输入 \(N\) 个模式串，举个栗子：hit,her,his,she。首先建立一棵 trie 树。

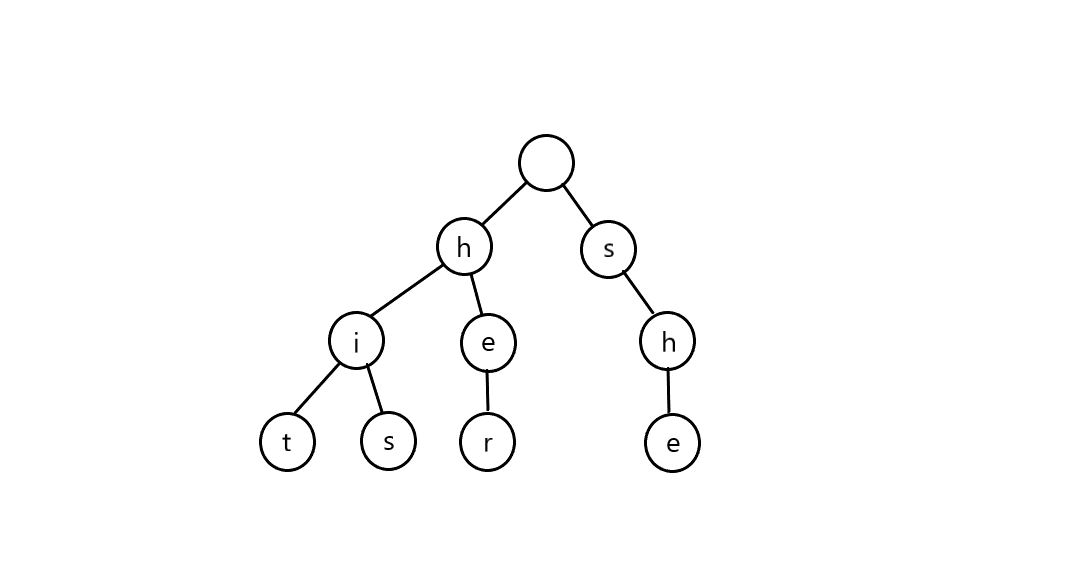
就是酱紫的啦。

然后 ... 。我们来一个神奇的操作：

\(fail\) 是失配指针，注意是失配意味着如果此时匹配失败，那么我们就要到达这个指针指向的位置继续常数匹配。

所以，我们可以将失配指针指向的的节点理解为：

当前节点所代表的串，最长的、能与后缀匹配的，在 trie 中出现过的前缀所代表的节点。

所以，\(fail\) 指针类似于 KMP 的 \(next[]\) 数组，只不过由单串变为了多串而已。

加入失配指针后就是酱紫：

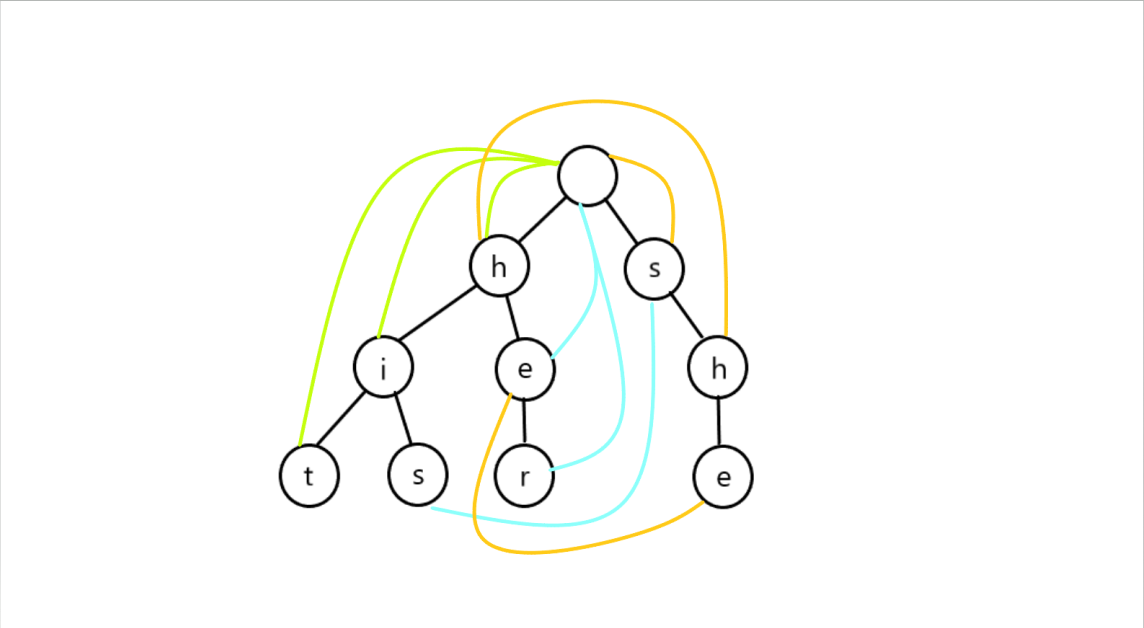
看起来很乱但是很有用的啦，虽然画在了这里但是并不知道怎么求对不对。

我们先看看这个指针是要干什么吧。

每次沿着 Trie 树匹配，匹配到当前位置没有匹配上时，直接跳转到失配指针所指向的位置继续进行匹配。

然后 dalao 们的 blog 告诉我们 Trie 树的失配指针是：

指向沿着其父节点的失配指针，一直向上，直到找到拥有当前这个字母的子节点的节点的那个子节点。

看不懂？那就继续往下看吧。

AC 自动机·原理分析

简单说就是在 trie 树上跑 KMP，那么显然最难的地方就是找失配指针。（就是上面那个五颜六色的东东）

如果您确保已经理解了 KMP 的 \(next[]\) 数组的含义的话，这就很好理解了。

这就是在失配之后应该去的地方，也因为有这个数组的存在，才让 AC 自动机有了如此高的效率。

这个只能意会而不可言传，理解起来比较难，强烈推荐读者自行画图理解。（或借助上图理解）

然后是匹配，其实匹配的过程十分简单，直接讲述一下即可首先。

指针指向根节点依次读入单词，检查是否存在这个子节点。

然后指针跳转到子节点，如果不存在，直接跳转到失配指针即可。

是不是感觉和 KMP 好像的样子。

AC 自动机·代码实现

显示模板式的 trie 插入：

void insert(string s){

	int p=1,len=s.length();

	for(int i=0;i<len;i++){

		int ch=s[i]-'a';

		if(!trie[p][ch]) trie[p][ch]=++tot;

		p=trie[p][ch];

	}

	sum[p]++;//注意一下可能有重复串。

	return;

}

然后是最重要的 \(get\_fail()\) 函数，详情请见注释：

void get_fail(){

	queue<int>q;

	for(int i=0;i<26;i++){//第二层的fail指针提前处理一下。

		if(!trie[1][i]) continue;

		q.push(trie[1][i]);//加入队列，进行 BFS。

		fail[trie[1][i]]=1;//将第二层的 fail 指针指向根节点。

	}

	while(!q.empty()){

		int now=q.front();

		q.pop();

		for(int i=0;i<26;i++){//枚举所有子节点。

			if(trie[now][i]){//存在这个子节点。

				fail[trie[now][i]]=trie[fail[now]][i];

                //子节点的 fail 指针指向当前节点的。

                //fail 指针所指向的节点的相同子节点。

				q.push(trie[now][i]);//入队。

			}

			else trie[now][i]=trie[fail[now]][i];//不存在这个子节点。

            //当前节点的这个子节点指向当前节点 fail 指针的这个子节点。

            //唯一变化是没有入队。（根本不存在为什么要 BFS 对吧）

		}

	}

	return;

}

然后是匹配的代码：

int AC_ask(string a){

	int p=1,ans=0,len=a.length();

	for(int i=0;i<len;i++){//根据匹配串的字符进行遍历。

		p=trie[p][a[i]-'a'];

		for(int j=p;j && sum[j]!=-1;j=fail[j]){//对每一个字符进行遍历。

            //注意一下循环条件，第一个是没有指向空（j），第二个是之前没有遍历过（sun[j]!=-1）

            //注意之后不是 j++，而是 j=fail[j]，即走到自己的 fail 指针，直到其为空。

			ans+=sum[j];//统计答案。

            sum[j]=-1;//将其标记为已经经过，不用进行重复遍历。

		}

	}

	return ans;//返回答案。

}

最后是 main 函数的代码：

int n,trie[N][30],sum[N],fail[N],tot=1;

string s,a;

int main(){

	scanf("%d",&n);

	for(int i=1;i<=n;i++){

		cin>>s;

		insert(s);//插入。

	}

	cin>>a;

	get_fail();//找 fail[] 指针。

	printf("%d\n",AC_ask(a));//输出。

    return 0;

}

AC 自动机·更进一步

其实...就是多做题，没有什么窍门的好吗。

然后先是模板题，用上面的代码就可以过了。

第一题

#10057 「一本通 2.4 例 1」Keywords Search

裸题？确实是裸题，不讲了。

#include <cstdio>

#include <algorithm>

#include <cstring>

#include <cmath>

#include <iostream>

#include <queue>

#define N 10010

#define M 1000010

using namespace std;

int n, T, trie[N][30], cnt[N], fail[N], tot = 1;

long long ans = 0;

char s[N], a[M];

int read() {

    int x = 0, f = 1;

    char c = getchar();

    while (c < '0' || c > '9') f = (c == '-') ? -1 : 1, c = getchar();

    while (c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();

    return x * f;

}

void insert(char* a) {

    int p = 1, len = strlen(a);

    for (int i = 0; i < len; i++) {

        int ch = a[i] - 'a';

        if (!trie[p][ch])

            trie[p][ch] = ++tot;

        p = trie[p][ch];

    }

    cnt[p]++;

    return;

}

void get_fail() {

    queue<int> q;

    for (int i = 0; i < 26; i++) {

        if (!trie[1][i]) {

            trie[1][i] = 1;

            continue;

        }

        fail[trie[1][i]] = 1;

        q.push(trie[1][i]);

    }

    while (!q.empty()) {

        int now = q.front();

        q.pop();

        for (int i = 0; i < 26; i++) {

            if (trie[now][i]) {

                fail[trie[now][i]] = trie[fail[now]][i];

                q.push(trie[now][i]);

            } else

                trie[now][i] = trie[fail[now]][i];

        }

    }

    return;

}

void AC_find(char* a) {

    int p = 1, len = strlen(a);

    for (int i = 0; i < len; i++) {

        p = trie[p][a[i] - 'a'];

        for (int j = p; j && cnt[j] != -1; j = fail[j]) {

            ans += cnt[j];

            cnt[j] = -1;

        }

    }

    return;

}

int main() {

    T = read();

    while (T--) {

        tot = 1;

        ans = 0;

        memset(trie, 0, sizeof(trie));

        memset(cnt, 0, sizeof(cnt));

        memset(fail, 0, sizeof(fail));

        n = read();

        for (int i = 1; i <= n; i++) {

            scanf("%s", s);

            insert(s);

        }

        get_fail();

        scanf("%s", a);

        AC_find(a);

        printf("%lld\n", ans);

    }

    return 0;

}

第二题

#10058 「一本通 2.4 练习 1」玄武密码

又是裸题？至少需要一点技巧了。

一开始的想法是 vector + AC 自动机暴力统计，发现 20 分 TLE 滚粗。

所以怎么办？方法如下：

根据传统的 AC 自动机，在 trie 树上跑母串。
每到一个点就标记它的每一个 \(fail[]\) 指针。（包括他本身）
统计答案时，从每个单词的最下方往前跳，第一个被标记的节点的下标即为答案。

证明略。（你都是打 AC 自动机的人了，至少是提高组吧，这点水平应该还是有的）

#include <cstdio>

#include <algorithm>

#include <cmath>

#include <iostream>

#include <cmath>

#include <queue>

#include <cstring>

#define N 10000010

#define M 100010

using namespace std;

int ch[50], n, m, tot = 0;

int trie[N][5], fail[N], end[M], l[M], pre[N], flag[N];

char a[N], s[110];

void insert(char* a, int x) {

    int p = 0, len = strlen(a);

    l[x] = len;

    for (int i = 0; i < len; i++) {

        int c = ch[a[i] - 'A'];

        if (!trie[p][c]) {

            trie[p][c] = ++tot;

            pre[tot] = p;

        }

        p = trie[p][c];

    }

    end[x] = p;

    return;

}

void get_fail() {

    queue<int> q;

    for (int i = 0; i < 4; i++)

        if (trie[0][i])

            fail[trie[0][i]] = 0, q.push(trie[0][i]);

    while (!q.empty()) {

        int now = q.front();

        q.pop();

        for (int i = 0; i < 4; i++) {

            if (trie[now][i]) {

                fail[trie[now][i]] = trie[fail[now]][i];

                q.push(trie[now][i]);

            } else

                trie[now][i] = trie[fail[now]][i];

        }

    }

    return;

}

void AC_work() {

    int len = strlen(a), p = 0;

    for (int i = 0; i < len; i++) {

        p = trie[p][ch[a[i] - 'A']];

        int k = p;

        while (k > 1) {

            if (flag[k])

                break;

            flag[k] = true;

            k = fail[k];

        }

    }

    return;

}

int get_ans(int x) {

    int p = end[x];

    for (int i = l[x]; i; i--) {

        if (flag[p])

            return i;

        p = pre[p];

    }

    return 0;

}

int main() {

    memset(flag, false, sizeof(flag));

    ch['N' - 'A'] = 0;

    ch['S' - 'A'] = 1;

    ch['W' - 'A'] = 2;

    ch['E' - 'A'] = 3;

    scanf("%d %d", &n, &m);

    scanf("%s", a);

    for (int i = 1; i <= m; i++) {

        scanf("%s", s);

        insert(s, i);

    }

    get_fail();

    AC_work();

    for (int i = 1; i <= m; i++) printf("%d\n", get_ans(i));

    return 0;

}

第三题

#10059 「一本通 2.4 练习 2」Censoring

裸题？不存在的。

经典的 AC 自动机 + 栈的题目，还记得我们做过一道 KMP + 栈的题目吗。（不记得）

类似的，在 AC 自动机的同时用栈维护即可啦。

#include <cstdio>

#include <algorithm>

#include <cmath>

#include <iostream>

#include <cstring>

#include <queue>

#define N 100010

using namespace std;

int n, trie[N][30], fail[N], jl[N], sk[N], tot = 0, cnt = 0, ed[N];

char s[N], t[N], ans[N];

void insert(char* a) {

    int p = 0, len = strlen(a);

    for (int i = 0; i < len; i++) {

        int ch = a[i] - 'a';

        if (!trie[p][ch])

            trie[p][ch] = ++tot;

        p = trie[p][ch];

    }

    ed[p] = len;

    return;

}

void get_fail() {

    queue<int> q;

    for (int i = 0; i < 26; i++)

        if (trie[0][i])

            fail[trie[0][i]] = 0, q.push(trie[0][i]);

    while (!q.empty()) {

        int now = q.front();

        q.pop();

        for (int i = 0; i < 26; i++) {

            if (trie[now][i]) {

                fail[trie[now][i]] = trie[fail[now]][i];

                q.push(trie[now][i]);

            } else

                trie[now][i] = trie[fail[now]][i];

        }

    }

    return;

}

void AC_work() {

    int p = 0, len = strlen(s);

    for (int i = 0; i < len; i++) {

        p = trie[p][s[i] - 'a'];

        jl[i] = p;

        sk[++cnt] = i;

        if (ed[p]) {

            cnt -= ed[p];

            p = jl[sk[cnt]];

        }

    }

    return;

}

int main() {

    memset(ed, 0, sizeof(ed));

    scanf("%s", s);

    scanf("%d", &n);

    for (int i = 1; i <= n; i++) {

        scanf("%s", t);

        insert(t);

    }

    get_fail();

    AC_work();

    for (int i = 1; i <= cnt; i++) printf("%c", s[sk[i]]);

    printf("\n");

    return 0;

}

从 AC 自动机到 fail 树

回忆AC自动机的匹配过程：

将文本串送入AC自动机，每到达一个结点 u 就从 u 开始不断跳 fail直到根。

期间跳到的结点代表的串都在文本串中出现。

可以从文本串的每位开始向上跳 fail 找模式串结尾结点，那同样能从模式串结尾结点开始逆着fail找文本串节点。

即从某个模式串结尾结点开始不断逆着跳 fail，期间跳到的文本串的结点个数就是这个模式串在文本串中出现的次数。

依据这个思想在 Trie 树上构造好 fail 指针后，只留下反向的fail指针作为边，就得到了 fail 树。

为什么是树？因为原本每个节点只有一个 fail 指针，所以构造出的一定是树的结构。

fail 树有个很好的性质：

将 fail 树上每个属于文本串的结点权值置为1，那么结点 u 的子树总权值就是 u 代表的串在文本串中出现的次数。

而求子树权值和很容易想到DFS序+树状数组，这样复杂度就大大下降，这就是 fail 树解题的常见套路。

例题一

fail 树模板

既然是模板就没什么好讲的啦，就是将上面的话转化为代码而已。（这里用 DFS 求子树权值，因为数据范围小）

#include<cstdio>

#include<cstring>

#include<cmath>

#include<iostream>

#include<algorithm>

#include<queue>

#define N 200010

#define M 2000010

using namespace std;

int n,trie[N][30],fail[N],sum[N],match[N],tot=0;

int head[N],cnt=0;

struct node{

	int nxt,to;

}edge[N];

char t[N],s[M];

void insert(char* a,int x){

	int p=0,len=strlen(a);

	for(int i=0;i<len;i++){

		int ch=a[i]-'a';

		if(!trie[p][ch]) trie[p][ch]=++tot;

		p=trie[p][ch];

	}

	match[x]=p;

	return;

}

void get_fail(){

	queue<int>q;

	for(int i=0;i<26;i++)

		if(trie[0][i]) fail[trie[0][i]]=0,q.push(trie[0][i]);

	while(!q.empty()){

		int now=q.front();q.pop();

		for(int i=0;i<26;i++) if(trie[now][i]){

			fail[trie[now][i]]=trie[fail[now]][i];

			q.push(trie[now][i]);

		}

		else trie[now][i]=trie[fail[now]][i];

	}

	return;

}

void addedge(int x,int y){

	++cnt;

	edge[cnt].nxt=head[x];

	edge[cnt].to=y;

	head[x]=cnt;

	return;

}

void dfs(int x){

	for(int i=head[x];i;i=edge[i].nxt){

		int y=edge[i].to;

		dfs(y);

		sum[x]+=sum[y];

	}

	return;

}

int main(){

	scanf("%d",&n);

	for(int i=1;i<=n;i++){scanf("%s",t);insert(t,i);}

	get_fail();

	scanf("%s",s);

	int p=0,len=strlen(s);

	for(int i=0;i<len;i++){

		p=trie[p][s[i]-'a'];

		++sum[p];

	}

	for(int i=1;i<=tot;i++) addedge(fail[i],i);

	dfs(0);

	for(int i=1;i<=n;i++) printf("%d\n",sum[match[i]]);

	return 0;

}

例题二

[TJOI2013]单词

因为题目中所有的模式串=文本串，所以本题甚至连 fail 树都不用建。

同样的运用 fail 树的思想，通过逆 BFS 序统计答案即可。

为什么是逆 BFS 序？其实就是从下往上想根节点集中，也就是上面的统计子树大小。

但是由于本题的特殊性质（所有的模式串=文本串），只要一个循环就可以搞定了。

#include <cstdio>

#include <algorithm>

#include <cmath>

#include <iostream>

#include <cstring>

#define N 1000010

using namespace std;

int n, trie[N][30], fail[N], sum[N], match[N];

int tot = 0, head, tail, q[N];

char s[N];

void insert(char* a, int x) {

    int p = 0, len = strlen(a);

    for (int i = 0; i < len; i++) {

        int ch = a[i] - 'a';

        if (!trie[p][ch])

            trie[p][ch] = ++tot;

        p = trie[p][ch];

        sum[p]++;

    }

    match[x] = p;

    return;

}

void get_fail() {

    tail = head = 0;

    for (int i = 0; i < 26; i++)

        if (trie[0][i])

            fail[trie[0][i]] = 0, q[++tail] = trie[0][i];

    while (head < tail) {

        int now = q[++head];

        for (int i = 0; i < 26; i++)

            if (trie[now][i]) {

                fail[trie[now][i]] = trie[fail[now]][i];

                q[++tail] = trie[now][i];

            } else

                trie[now][i] = trie[fail[now]][i];

    }

    return;

}

int main() {

    scanf("%d", &n);

    for (int i = 1; i <= n; i++) {

        scanf("%s", s);

        insert(s, i);

    }

    get_fail();

    for (int i = tail; i >= 0; i--) sum[fail[q[i]]] += sum[q[i]];

    for (int i = 1; i <= n; i++) printf("%d\n", sum[match[i]]);

    return 0;

}

结语

之前说了，我的了解只是皮毛。

想要更进一步的话，可以去看看集训队的论文。（2004 多串匹配算法及其启示——朱泽园）

网上应该是搜的到的，如果没有可以私信或者 QQ 找我要，我会不会回就看情况了。（QQ 自己去翻这篇文章）

注意，本文部分解释和我的 AC 自动机启蒙来自yyb 神犇的文章，侵权请删。

完结撒花。

浅析 AC 自动机的更多相关文章

AC自动机及KMP练习
好久都没敲过KMP和AC自动机了.以前只会敲个kuangbin牌板子套题.现在重新写了自己的板子加深了印象.并且刷了一些题来增加自己的理解. KMP网上教程很多,但我的建议还是先看AC自动机(Trie ...
基于trie树做一个ac自动机
基于trie树做一个ac自动机 #!/usr/bin/python # -*- coding: utf-8 -*- class Node: def __init__(self): self.value ...
AC自动机-算法详解
What's Aho-Corasick automaton? 一种多模式串匹配算法,该算法在1975年产生于贝尔实验室,是著名的多模式匹配算法之一. 简单的说,KMP用来在一篇文章中匹配一个模式串:但 ...
python爬虫学习(11) —— 也写个AC自动机
0. 写在前面本文记录了一个AC自动机的诞生! 之前看过有人用C++写过AC自动机,也有用C#写的,还有一个用nodejs写的.. C# 逆袭--自制日刷千题的AC自动机攻克HDU OJ HDU 自 ...
BZOJ 2434: [Noi2011]阿狸的打字机 [AC自动机 Fail树树状数组 DFS序]
2434: [Noi2011]阿狸的打字机 Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 2545 Solved: 1419[Submit][Sta ...
BZOJ 3172: [Tjoi2013]单词 [AC自动机 Fail树]
3172: [Tjoi2013]单词 Time Limit: 10 Sec Memory Limit: 512 MBSubmit: 3198 Solved: 1532[Submit][Status ...
BZOJ 1212: [HNOI2004]L语言 [AC自动机 DP]
1212: [HNOI2004]L语言 Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 1367 Solved: 598[Submit][Status ...
[AC自动机]【学习笔记】
Keywords Search Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)To ...
AC自动机 HDU 3065
大概就是裸的AC自动机了 #include<stdio.h> #include<algorithm> #include<string.h> #include< ...

随机推荐

Copy As HTML From VSCode
JS生成可自定义语法高亮HTMLcode cnblogs @ Orcim !deprecated! 这里有更好的方案,具体看我的这篇博客博客代码高亮的另一种思路这篇文章介绍了如何在博客里插入一段 ...
07 Sublime Text3常用快捷键
通用常用类(General) ↑↓←→:上下左右移动光标,注意不是不是 KJHL ! Alt:调出菜单 Ctrl + Shift + P:调出命令板(Command Palette) Ctrl + ` ...
Java知识系统回顾整理01基础01第一个程序01JDK 安装
一.首先第一步看JDK配置成功后的效果点WIN键->运行(或者使用win+r) 输入cmd命令输入java -version 注: -version是小写,不能使用大写,java后面有一个空 ...
03 Comments in C Programming C编程中的注释
Comments 注释简介 Let's take a quick break from programming and talk about comments. Comments help progr ...
【题解】【POI2000】病毒
题目链接这题让我们构造一个无限长的,不包括给定字符串的01串. 把给定字符串放到\(AC\)自动机上,在结尾处打上标记. 发现,如果我们要构造一个无限长的串,必然要有一个环. 那么这个环上就一定不能 ...
java -inally转
1.不管有木有出现异常,finally块中代码都会执行: 2.当try和catch中有return时,finally仍然会执行:3.finally是在return后面的表达式运算后执行的(此时并没有返 ...
多测师讲解selenium—自动化测试课堂面试题总结—高级讲师肖sir
1.你有做过自动化?你用什么语言? python2.自动化中如何使用语言打开一个网址?浏览器,浏览器对应驱动,导入库,类,get,url3.在一个浏览器中打开多个窗口?open_windows dri ...
MeteoInfoLab脚本示例：读取文本文件
此例中的降水文本文件下载自"中国气象科学数据共享服务网"(http://cdc.nmic.cn/sksj.do?method=ssrjscp),其实是ESRI的文本格点数据格式.对 ...
微信小程序 - 重置checkbox样式
/* 未选中的背景样式 */ checkbox .wx-checkbox-input { border-radius: 50%;/* 圆角 */ width: 30rpx; /* 背景的宽 */ h ...
net core 微服务快速开发框架 Viper 初体验2020-10-17
1.Viper是什么? Viper 是.NET平台下的Anno微服务框架的一个示例项目.入门简单.安全.稳定.高可用.全平台可监控.底层通讯可以随意切换thrift grpc. 自带服务发现.调用链追 ...

浅析 AC 自动机

简述