【Codeforces】CF Round #592 (Div. 2) - 题解

Problem - A

Tomorrow is a difficult day for Polycarp: he has to attend \(a\) lectures and \(b\) practical classes at the university! Since Polycarp is a diligent student, he is going to attend all of them.

While preparing for the university, Polycarp wonders whether he can take enough writing implements to write all of the lectures and draw everything he has to during all of the practical classes. Polycarp writes lectures using a pen (he can't use a pencil to write lectures!); he can write down \(c\) lectures using one pen, and after that it runs out of ink. During practical classes Polycarp draws blueprints with a pencil (he can't use a pen to draw blueprints!); one pencil is enough to draw all blueprints during \(d\) practical classes, after which it is unusable.

Polycarp's pencilcase can hold no more than \(k\) writing implements, so if Polycarp wants to take \(x\) pens and \(y\) pencils, they will fit in the pencilcase if and only if \(x+y \leq k\).

Now Polycarp wants to know how many pens and pencils should he take. Help him to determine it, or tell that his pencilcase doesn't have enough room for all the implements he needs tomorrow!

Note that you don't have to minimize the number of writing implements (though their total number must not exceed \(k\)).

题意

给定 \(a,b,c,d,k\)

求一对 \(x,y\) 使 \(cx \geq a,dy \geq b\) 且 \(x+y \leq k\)。

思路

模拟即可。

代码

#include <bits/stdc++.h>
int t,a,b,c,d,k;
int main() {
	for (scanf("%d",&t);t--;) {
		int x = -1,y = -1;
		scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
		for (int i = 0;i <= k;i++)
			for (int j = 0;i+j <= k;j++)
				if (c*i >= a && d*j >= b) {
					x = i,y = j;
					break;
				}
		if (x == -1) printf("-1\n");
		else printf("%d %d\n",x,y);
	}
	return 0;
}

Problem - B

Nikolay lives in a two-storied house. There are \(n\) rooms on each floor, arranged in a row and numbered from one from left to right. So each room can be represented by the number of the floor and the number of the room on this floor (room number is an integer between \(1\) and \(n\)).

If Nikolay is currently in some room, he can move to any of the neighbouring rooms (if they exist). Rooms with numbers \(i\) and \(i+1\) on each floor are neighbouring, for all \(1≤i≤n−1\). There may also be staircases that connect two rooms from different floors having the same numbers. If there is a staircase connecting the room \(x\) on the first floor and the room \(x\) on the second floor, then Nikolay can use it to move from one room to another.

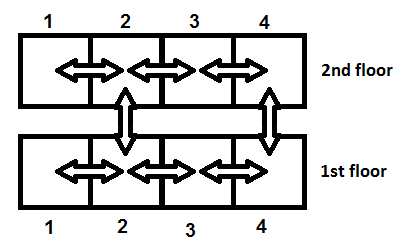
The picture illustrates a house with \(n=4\). There is a staircase between the room \(2\) on the first floor and the room \(2\) on the second floor, and another staircase between the room \(4\) on the first floor and the room \(4\) on the second floor. The arrows denote possible directions in which Nikolay can move. The picture corresponds to the string "0101" in the input.

Nikolay wants to move through some rooms in his house. To do this, he firstly chooses any room where he starts. Then Nikolay moves between rooms according to the aforementioned rules. Nikolay never visits the same room twice (he won't enter a room where he has already been).

Calculate the maximum number of rooms Nikolay can visit during his tour, if:

·he can start in any room on any floor of his choice,

·and he won't visit the same room twice.

题意

有一个两层的房子，每层有 \(n\) 间屋子，每层的相邻两个屋子可以到达。两层之间有一些屋子有电梯相连。

问从任意屋子开始，不经过重复屋子最多能经过多少屋子。

思路

开始的房屋肯定是第 \(1\) 间或 \(n\) 间（第一层或第二层都行），然后走到最远的电梯，经过的房屋数乘 \(2\)，取最大即可。

代码

#include <bits/stdc++.h>
using namespace std;
int t,n,S,T;
string s;
int main() {
	for (cin >> t;t--;) {
		S = -1;
		cin >> n >> s;
		for (size_t i = 0;i < s.size();i++)
			if (s[i] ==  '1') {
				T = i+1;
				if (S == -1) S = i+1;
			}
		if (S == -1) printf("%d\n",n);
		else printf("%d\n",max((n-S+1)*2,T*2));
	}
	return 0;
}

Problem - C

The football season has just ended in Berland. According to the rules of Berland football, each match is played between two teams. The result of each match is either a draw, or a victory of one of the playing teams. If a team wins the match, it gets \(w\) points, and the opposing team gets \(0\) points. If the game results in a draw, both teams get \(d\) points.

The manager of the Berland capital team wants to summarize the results of the season, but, unfortunately, all information about the results of each match is lost. The manager only knows that the team has played \(n\) games and got \(p\) points for them.

You have to determine three integers \(x, y\) and \(z\) — the number of wins, draws and loses of the team. If there are multiple answers, print any of them. If there is no suitable triple \((x,y,z)\), report about it.

题意

给定 \(n,p,w,d\)，求一个三元组 \((x,y,z)\) 使 \(x⋅w+y⋅d=p\) 且 \(x+y+z=n\)。

思路

暴枚就能过，讲道理枚举到 w 就够了。

代码

#include <cstdio>
using ll = long long;
ll n,p,d,w;
int main() {
    scanf("%lld%lld%lld%lld",&n,&p,&w,&d);
    for (ll a = 0;a < w && d*a <= p;a++) if (!((p-d*a)%w) && (p-d*a)/w+a <= n) return printf("%lld %lld %lld",(p-d*a)/w,a,n-(p-d*a)/w-a)*0;
    printf("-1");
    return 0;
}

Problem - D

You are given a tree consisting of \(n\) vertices. A tree is an undirected connected acyclic graph.

You have to paint each vertex into one of three colors. For each vertex, you know the cost of painting it in every color.

You have to paint the vertices so that any path consisting of exactly three distinct vertices does not contain any vertices with equal colors. In other words, let's consider all triples \((x,y,z)\) such that \(x≠y,y≠z,x≠z\), \(x\) is connected by an edge with \(y\), and \(y\) is connected by an edge with \(z\). The colours of \(x, y\) and \(z\) should be pairwise distinct. Let's call a painting which meets this condition good.

You have to calculate the minimum cost of a good painting and find one of the optimal paintings. If there is no good painting, report about it.

题意

给定一颗 \(n\) 个点的树，要给每个点染上 \(3\) 种颜色中的任意一种，相邻三个点不能有同色。每个点染上颜色 \(1,2,3\) 的代价都不同，求代价最小的合法染色方案。

思路

不难发现，给出的树不是链答案就是 -1，否则算一算 6 种情况的答案就行了。

代码

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll n,s,a[100001],b[100001],c[100001],deg[100001],p[100001],ans[100001];
vector<int> eg[100001];
ll ansx = 99999999999999999ll;
inline void dfs(int now,int fa,ll tot,ll A,ll B) {
	ll to = -1;
	for (size_t i = 0;i < eg[now].size();i++) if (eg[now][i] ^ fa) to = eg[now][i];
	if (to == -1) {
		if ((A == 1 || A == 2) && (B == 1 || B == 2)) p[now] = 3,tot += c[now];
		if ((A == 3 || A == 2) && (B == 3 || B == 2)) p[now] = 1,tot += a[now];
		if ((A == 1 || A == 3) && (B == 1 || B == 3)) p[now] = 2,tot += b[now];
		if (tot < ansx) {
			ansx = tot;
			for (int i = 1;i <= n;i++) ans[i] = p[i];
		}
		return;
	}
	if (!A && !B) {
		p[now] = 1,dfs(to,now,tot+a[now],1,0);
		p[now] = 2,dfs(to,now,tot+b[now],2,0);
		p[now] = 3,dfs(to,now,tot+c[now],3,0);
	}
	if (A && !B) {
		if (A == 1) {
			p[now] = 2,dfs(to,now,tot+b[now],A,2);
			p[now] = 3,dfs(to,now,tot+c[now],A,3);
		}
		if (A == 2) {
			p[now] = 1,dfs(to,now,tot+a[now],A,1);
			p[now] = 3,dfs(to,now,tot+c[now],A,3);
		}
		if (A == 3) {
			p[now] = 2,dfs(to,now,tot+b[now],A,2);
			p[now] = 1,dfs(to,now,tot+a[now],A,1);
		}
	}
	if (A && B) {
		if ((A == 1 || A == 2) && (B == 1 || B == 2)) p[now] = 3,dfs(to,now,tot+c[now],B,3);
		if ((A == 3 || A == 2) && (B == 3 || B == 2)) p[now] = 1,dfs(to,now,tot+a[now],B,1);
		if ((A == 1 || A == 3) && (B == 1 || B == 3)) p[now] = 2,dfs(to,now,tot+b[now],B,2);
	}
}
int main() {
	cin >> n;
	for (int i = 1;i <= n;i++) cin >> a[i];
	for (int i = 1;i <= n;i++) cin >> b[i];
	for (int i = 1;i <= n;i++) cin >> c[i];
	for (int i = 1,u,v;i < n;i++) {
		cin >> u >> v;
		eg[u].push_back(v);
		eg[v].push_back(u);
		deg[u]++;
		deg[v]++;
	}
	for (int i = 1;i <= n;i++) if (deg[i] > 2) return 0*printf("-1");
	for (int i = 1;i <= n;i++)
		if (deg[i] == 1) s = i;
	dfs(s,-1,0,0,0);
	cout << ansx<<endl;
	for (int i  = 1;i  <= n;i++) cout << ans[i] << ' ';
	return 0;
}

Problem - E

You are given a sequence \(a_1,a_2,…,a_n\) consisting of \(n\) integers.

You may perform the following operation on this sequence: choose any element and either increase or decrease it by one.

Calculate the minimum possible difference between the maximum element and the minimum element in the sequence, if you can perform the aforementioned operation no more than \(k\) times.

题意

给定一个数列，可以进行 \(k\) 次操作。每一次操作你可以将数列中的一个数加一或减一，问进行小于等于 \(k\) 次操作后数列中最大值减去最小值最小为多少。

思路

这个题直接维护左右两个指针，每次答案若要 \(-1\) 必须将所有最大值减一或所有最小值加一。搞花费小的就行了。

代码

#include <algorithm>
#include <iostream>
#include <cstdio>
using namespace std;
using ll = long long;
ll ans,n,k,l,r,a[100001];
int main(){
    cin >> n >> k;
    for (ll i = 1;i <= n;i++) cin >> a[i];
    sort(a+1,a+n+1); ans = a[n]-a[1];
    for (ll l = 1,r = n,x;l < r && k;ans -= x) k -= l < n-r+1 ? (x = min(a[l+1]-a[l],k/l))*l++ : (x = min(a[r]-a[r-1],k/(n-r+1)))*(n-r--)+x;
    cout << ans;
    return 0;
}

咕咕咕