【算法•日更•第五十七期】快速傅里叶变换（FFT）：从入门到放弃

▎一些用的上的东西

　　小编太菜了，很多东西都不会证明（主要是三角函数还没有学啊~~~）。

　　附上链接https://blog.csdn.net/enjoy_pascal/article/details/81478582

　　大家可以看看这个博主的证明。

　　所以小编就只提供讲解了。

▎前置知识

　　离散傅里叶变换，传送门。

▎FFT

　　在之前，一个多项式是长这个样子的：

　　

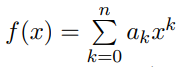
　　现在我们拆一下，定义两个多项式：

　　f₁(x)=a₀+a₂x+a₄x²+……+a_n-2x^n/2-1

　　f₂(x)=a₁+a₃x+a₅x²+……+a_n-1x^n/2-1

显然，f(x)=f₁(x²)+x·f₂(x²)。

　　

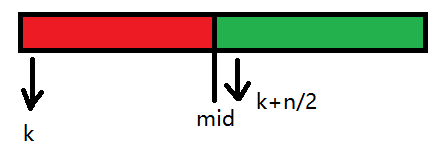
　　利用分治的思想，我们将ω_n^k和w_n^k+n/2分别当作x带入，易得：

　　f(ω_n^k)=f₁(ω_n/2^k)+ω_n^kf₂(ω_n/2^k)

　　f(w_n^k+n/2)=f₁(ω_n/2^k)-ω_n^kf₂(ω_n/2^k)

　　我们会发现只要算出f₁(ω_n/2^k)和ω_n^kf₂(ω_n/2^k)，f(ω_n^k)和f(w_n^k+n/2)就迎刃而解了。