牛客编程巅峰赛S2第4场

牛牛摆玩偶

题目描述

牛牛有$n(2 \leq n \leq 10^5)(2≤n≤105)$个玩偶，牛牛打算把这n个玩偶摆在桌子上，桌子的形状的长条形的，可以看做一维数轴。桌子上有 $M$ 个互不相交的区间$(1≤M≤10^5)$，这些区间上面可以放玩偶。一个位置只能放一个玩偶，玩偶之间的距离越大越美观，牛牛想最大化 D 的值，其中 D 为最近的两个玩偶之间的距离。请帮牛牛求出 D 的最大可能值。

示例1

输入

5,3,[[0,2],[4,7],[9,9]]

返回值

备注:

区间长度$\leq 2^{31} -1$

思路：

最大最小值，最小最大值，一看就是二分。比赛中就是过不了($90\%$的数据), 肯定思路没错，以为是数据错了(*^▽^*)。

思路数据没错，应该首先想到是不是时间复杂度太高，应该是judge函数的时间复杂度高了。下次一定注意。

代码

/**

 * struct Interval {

 *	int start;

 *	int end;

 *	Interval(int s, int e) : start(start), end(e) {}

 * };

 */

#define ll long long

const int maxn = 2e5+10;

class Solution {

public:

    /**

     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可

     *

     * @param n int整型 玩偶数

     * @param m int整型 区间数

     * @param intervals Interval类vector 表示区间

     * @return int整型

     */

    bool judge(ll x, vector<pair<ll, ll> > inv, int n){

        //n--;

        ll pos = -2e10;

        /*  复杂度太高？

        for(auto ine : inv){

            if(pos + x <= ine.first){

                pos = ine.first;

                n--;

            }

            if(n <= 0) return true;

            while(pos + x <= ine.second){

                pos += x;

                n--;

                if(n <= 0) return true;

            }

        }

        */

        for(auto in : inv){

            ll l = max(pos+x, in.first);

            if(l > in.second) continue;

            ll t = (in.second - l) / x;

            n -= (t+1);

            if(n <= 0) return true;

            pos = l + t*x;

        }

        return n <= 0;

    }

    int doll(int n, int m, vector<Interval>& intervals) {

        // write code here

        vector<pair<ll, ll> > inv;

        for(auto ine : intervals) {

            inv.push_back({1ll * ine.start, 1ll * ine.end});

        }

        sort(inv.begin(), inv.end(), [](const pair<ll, ll> &a, const pair<ll, ll> &b)->bool{

            return a.first < b.first;

        });

        ll l = 0, r = inv.back().second - inv[0].first;

        ll ans = -1;

        while(l <= r){

            ll mid = l + (r - l) / 2;

            if(judge(mid, inv, n)){

                ans = mid;

                l = mid + 1;

            }else r = mid - 1;

        }

        return ans;

    }

};

参数$a$为$vector<int>$，依次为$a_1,a_2,...,a_n$；

参数$query$为$vector<int>$，依次为$l_1,r_1,l_2,r_2,...,l_q,r_q$；

$n$为数组$a$长度，$q$为询问次数。

$30\%$ 数据满足 $1<=n,q<=1000$

$100\%$ 数据满足 $1<=n,q<=100000，1<=a_i<=100000，1<=l_i<=r_i<=n$

思路

没想出来，思路是听直播学的。

九九乘法表，划掉对角线，前缀和优化。

就是主对角线下面的等式之和，矩阵里对角线上面的元素和下面的元素和相同，故可以总体相加，如下图：

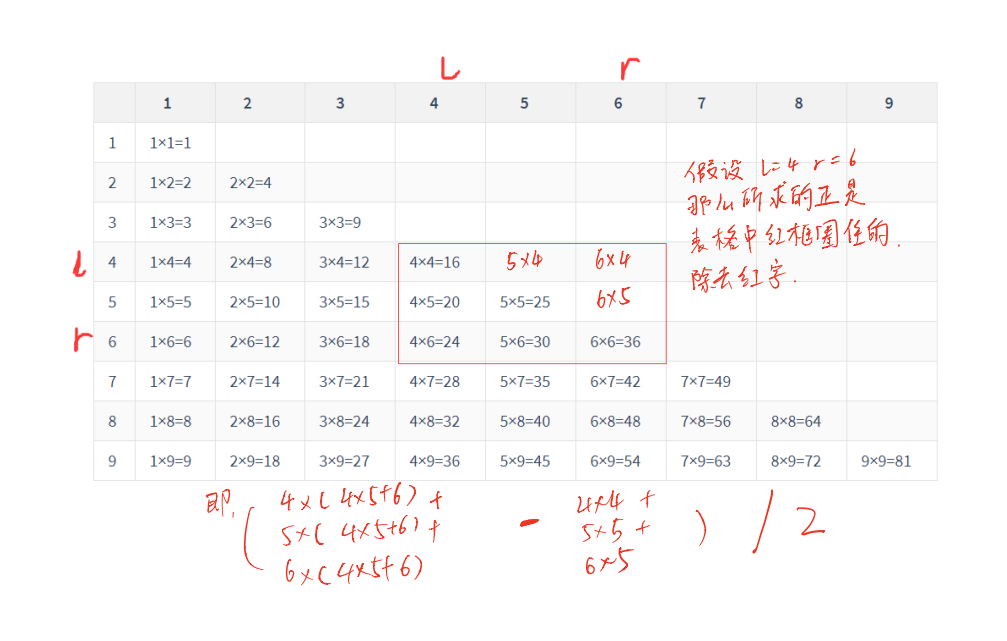
求和公式：$\sum_{i=l}^{r} \sum_{j=i+1}^{r} a_{i} * a_{j}=\frac{\left(\sum_{i=l}^{r} a_{i}\right)^{2}-\sum_{i=l}^{r} a_{i}^{2}}{2}$

另外：题目中数较大。需要开long long。用到了逆元的知识。

代码

#define ll long long

const int mod = 1e9+7;

const int maxn = 2e5+10;

ll sum[maxn], mul[maxn];

class Solution {

public:

    /**

     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可

     * 多次求交叉乘

     * @param a int整型vector a1,a2,...,an

     * @param query int整型vector l1,r1,l2,r2,...,lq,rq

     * @return int整型vector

     */

    vector<int> getSum(vector<int>& a, vector<int>& query) {

        // write code here

        sum[0] = mul[0] = 0;

        for(int i = 1; i <= a.size(); i++){

            sum[i] = (sum[i-1] + a[i-1]) % mod;

            mul[i] = (mul[i-1] + 1ll * a[i-1]*a[i-1] % mod) % mod;

        }

        vector<int> ans;

        for(int i = 0; i < query.size(); i+=2){

            int l = query[i], r = query[i+1];

            ll t = (sum[r] - sum[l-1]) % mod;

            ll res = (t * t % mod - (mul[r]-mul[l-1])% mod + mod)% mod ;

            res = (res * 500000004 % mod + mod) % mod;

            ans.push_back(res);

        }

        return ans;

    }

};