如何寻找决策最优解？熵权TOPSIS助你科学决策

熵权topsis是一种融合了熵值法与TOPSIS法的综合评价方法。熵值法是一种客观赋值法，可以减少主观赋值带来的偏差；而topsis法是一种常见的多目标决策分析方法，适用于多方案、多对象的对比研究，从中找出最佳方案或竞争力最强的对象。

熵权topsis是先由熵权法计算得到指标的客观权重，再利用TOPSIS法，对各评价对象进行评价。

熵权topsis法分析步骤通常可分为以下三步：

（1）数据标准化

（2）熵值法确定评价指标的权重

（3）topsis法得到评价对象的排名结果

其中第2、3步由SPSSAU自动计算输出。

一、研究背景

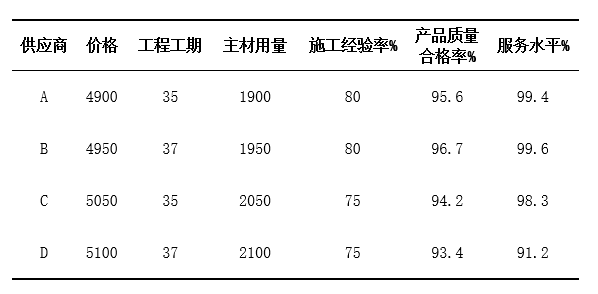
当前有一个项目进行招标，共有4个承包商，分别是A,B,C,D厂。由于招标需要考虑多个因素，各个方案指标的优劣程度也并不统一。为了保证评价过程中的客观、公正性。因此，考虑通过熵权TOPSIS法，对各个方案进行综合评价，从而选出最优方案。

二、操作步骤

（1）数据标准化

首先，需要对数据进行标准化处理。指标量纲（单位）不一致会造成不同指标的数据有大有小，这样会影响计算结果。为了消除量纲的影响，分析前需要先对数据进行处理。

正向指标：（X-Min）/(Max-Min) （生成变量-正向化MMS）

逆向指标：（Max-X）/(Max-Min) （生成变量-逆向化NMMS）

具体标准化的处理方式有很多种，具体结合文献和自身数据选择使用即可。不同的处理方式肯定会带来不同的结果，但结论一般不会有太大的偏倚。

本案例中，价格、工程工期、主材用量均为逆向指标；施工经验率、产品质量合格率、服务水平均为正向指标。按上述步骤分别对正向指标、逆向指标进行标准化处理。

（2）熵权TOPSIS法

选择【综合评价】--【熵权TOPSIS】。

将指标项放入【评价指标】框中，点击开始分析。

三、结果分析

（1）熵值法确定权重

上表是通过熵值法计算得出的6个指标权重，可以看出指标权重分布相对较为均匀。

各项指标的权重={0.1415, 0.2366, 0.1415, 0.1415, 0.2366, 0.1433, 0.1004}。

这一步仅仅得到了指标权重，熵值TOPSIS的核心在于TOPSIS法计算出相对接近度。权重值与数据相乘，得到新数据newdata，这一过程是SPSSAU自动完成，利用newdata进行TOPSIS法计算。

（2）topsis法得到每组样本的竞争力排名

从上表可知，利用熵权法后加权生成的数据(由SPSSAU算法自动完成)进行TOPSIS分析，针对6个指标进行TOPSIS评价。最终计算得出各评价对象与最优方案的接近程度(C值)，并对C值进行排序，得到最优方案。

根据结果显示，A厂（评价对象1）是最佳的供应商选择，其次为B厂。

四、其他说明

（1）分析之前是否需要进行标准化、归一化、正向化或逆向化处理等？

如果原始数据中有负向指标（数字越大反而越不好的意思），需要针对此类指标先‘逆向化’处理。当确认所有指标均为正向指标（数字越大越好的意思）后，需要接着进标准化处理。

数据进行标准化处理目的在于解决量纲问题，标准化处理的方式有很多，常见是‘归一化’，‘区间化’，‘均值化’，‘求和归一化’，‘平方和归一化’等等非常多。如果指标数据全部都大于0，SPSSAU建议是使用‘均值化’处理，如果指标数据有小于或等于0的数据，SPSSAU建议使用‘区间化’（默认将数据压缩成1~2之间）。

（2）如果分析数据中有负数或者0值如何办？

如果分析数据有负数或者0，这会导致无法进行熵值法计算，SPSSAU算法默认会进行‘非负平移’处理。SPSSAU非负平移功能是指，如果某列（某指标）数据出现小于等于0，则让该列数据同时加上一个‘平移值’【该值为某列数据最小值的绝对值+0.01】，以便让数据全部都大于0，因而满足算法要求。

以上就是本次分享内容，登录SPSSAU官网了解更多内容。