Git Best Practice All In One

Git Best Practice All In One

git workflow

本地开发环境：

开发人员自测的，可以是自己本地部署的静态服务器，当然也可类似是运行 npm server类似的环境，本地环境运行的代码可以是任何分支的

dev开发环境：

这个环境是用开发分支dev产出的代码来部署的，唯一的公用的

测试&预发布环境：

这个环境是用开发分支release产出的代码来部署的，唯一的公用的

线上生产环境：

这个环境是用开发分支master产出的代码来部署的，唯一的公用的

git 分支模型

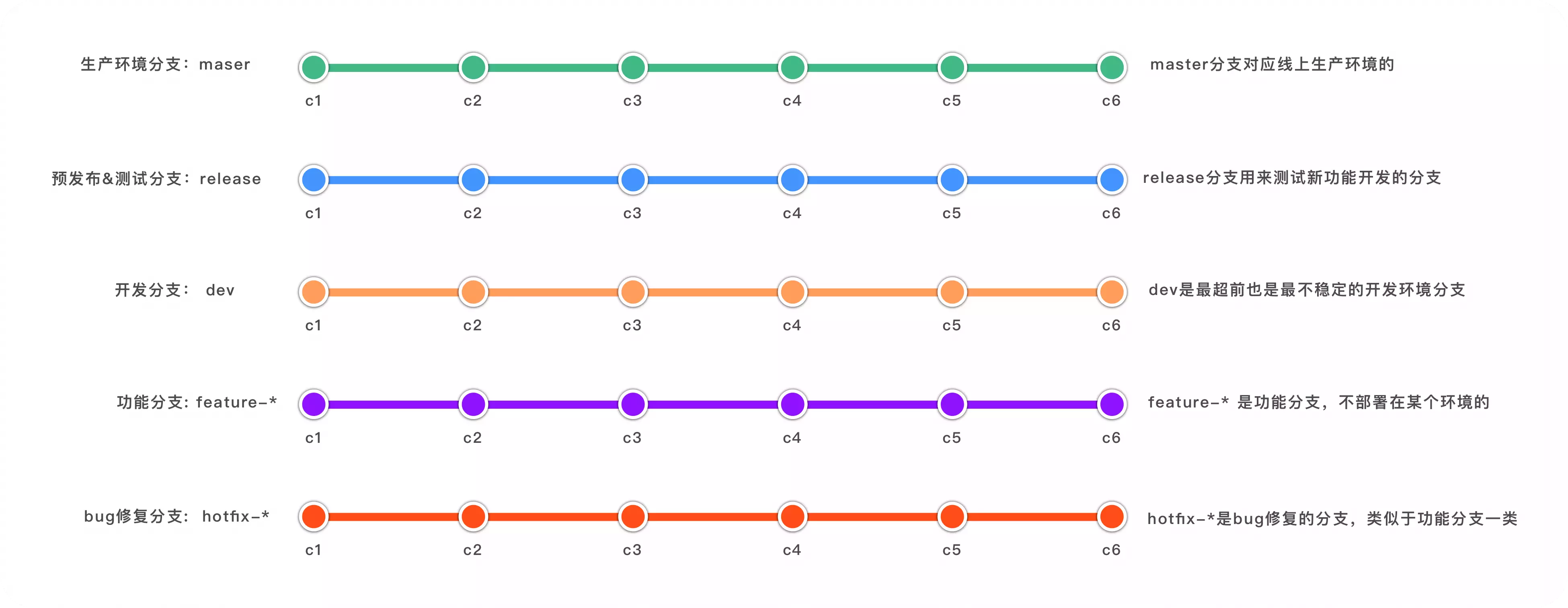
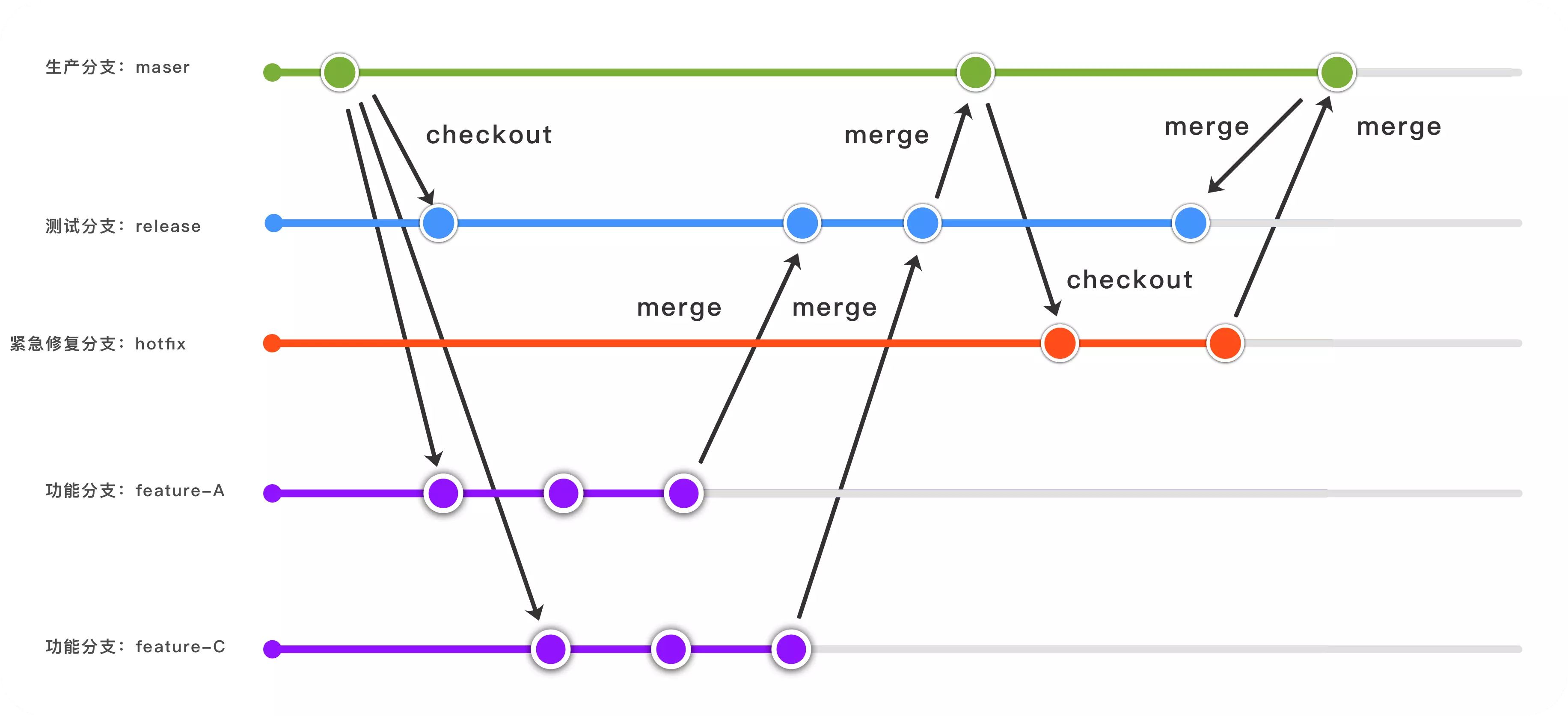
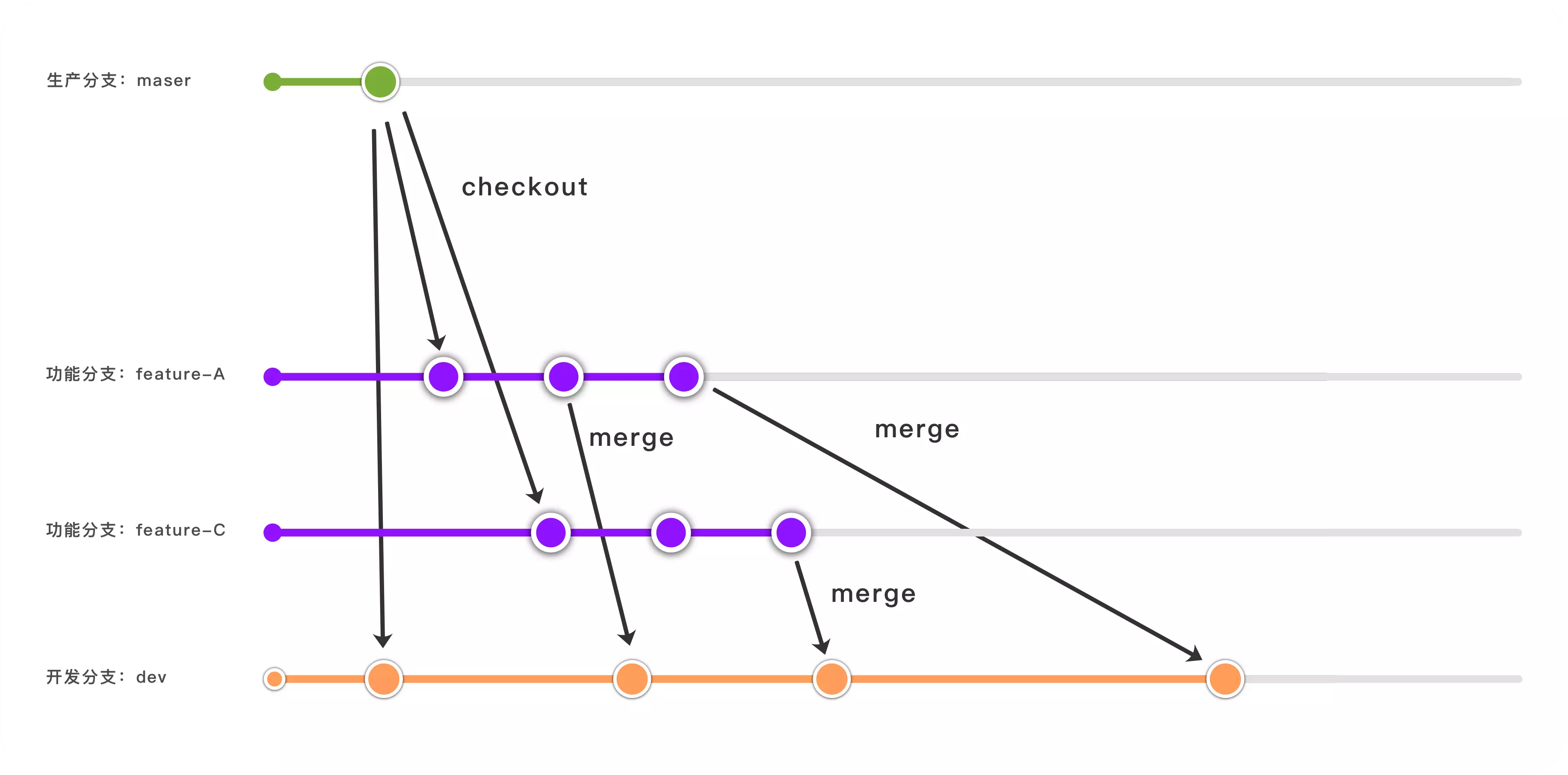
1. 所有的分支都是基于master分支检出

master ：保护分支，对应的就是生产环境的分支

release：保护分支，所有开发完成的分支会申请合并到release分支，提供给测试人员测试

feature--名字拼音缩写：功能分支，具体功能开发，（ 名字拼音缩写 ，方便定位某个开发人员，快速解决冲突问题，feature-fe-monitor-xgqfrms 或 feature/fe-monitor-xgqfrms）

dev：开发分支 & 脏分支( 不要 merge 到 feature 分支)，对应的是大家共用的开发环境，上面的代码会部署到一个公共的开发环境，供开发人员做自测，应付一些日常、非日常的调试

hotfix-：bug紧急修复分支，可以直接合并到master，

（假如release合并了几个feature分支，正在测试的情况下，发现需要紧急修复的buf，紧急修复测试完毕后，可以直接合并到master，如果合并到release，在由release合并到master，那些正在测试的功能或者还不准备上线的功能就会跟着直接上线了）

1. 工作流程

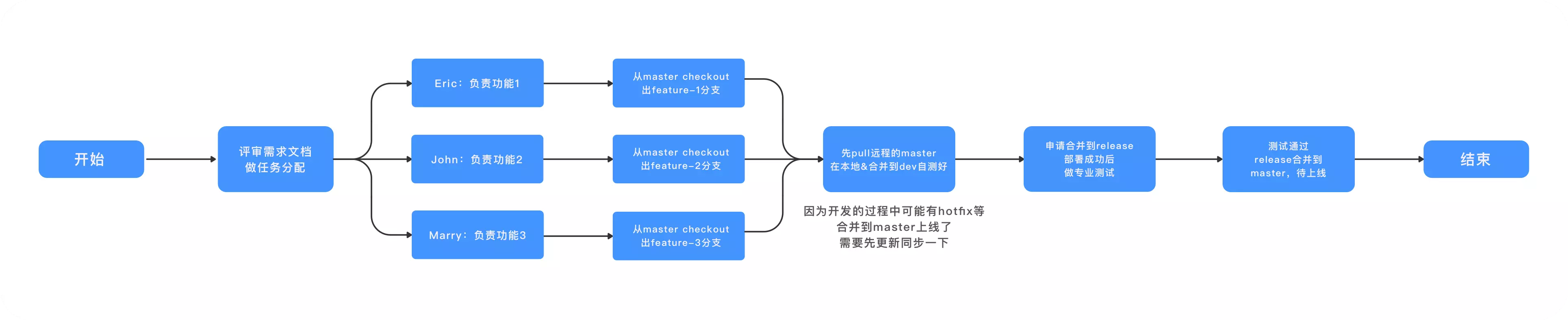
接到需求文档，做评审后分配个每个人或小组的功能开发，相关人员从master 检出 feature 功能分支

开发的时候除了会在本地测试，有需要还会合并到 dev分支，在公共的开发环境去自己做测试

因为在开发功能的期间，可能有 hotfix完成合并到master，合并代码的时候习惯 merge一下master，防止冲突等

自测完成之后，申请合并到 release，合并成功后部署到测试环境后通知测试人员做测试

测试通过后，release 申请合并到master，准备上线

如果测试不通过，在功能分支修改后重新 merge

上线成功稳定后删除对应的功能分支，dev 合并最新的master分支

一线大厂 git 分支流程

https://www.infoq.cn/article/EaC4c6yiJrzZ_Gtaf9Ne

https://zhuanlan.zhihu.com/p/45157955

http://yr87.cn/jxadd/article_detail/16393

https://biolxy.github.io/2018/12/04/Git-develop-SOAP/

refs

https://segmentfault.com/a/1190000024453209

music

NCS · Alan Walker - Fade [NCS Release]

---

---

xgqfrms 2012-2020

www.cnblogs.com 发布文章使用：只允许注册用户才可以访问！

---