题解：SDOI2017 新生舞会

Description

学校组织了一次新生舞会，Cathy 作为经验丰富的老学姐，负责为同学们安排舞伴。

有 $n$ 个男生和 $n$ 个女生参加舞会。一个男生和一个女生一起跳舞，互为舞伴。

Cathy 收集了这些同学之间的关系，比如两个人之前认不认识，计算得出 $a_{i,j}$ ，表示第 $i$ 个男生和第 $j$ 个女生一起跳舞获得的愉快程度。

Cathy 还需要考虑两个人一起跳舞是否方便，比如身高体重差别会不会太大，计算得出 $b_{i,j}$ ，表示第 $i$ 个男生和第 $j$ 个女生一起跳舞时的不协调程度。

一个方案中有 $n$ 对舞伴，假设每对舞伴的愉快程度分别为 $a'_1,a'_2,\dots,a'_n$ ，不协调程度分别为 $b'_1,b'_2,\dots,b'_n$ ，

我们令

\[\large
C = \frac{\sum_{i = 1}^{n} a'_i}{\sum_{i = 1}^{n} b'_i}
\]

Cathy 希望方案的 C 值最大。

当然，还需要考虑许多其他问题。

Cathy 想先用一个程序通过 $a_{i,j}$ 和 $b_{i,j}$ 求出一种方案，再手动对方案进行微调。

Cathy 找到你，希望你帮她写那个程序。

$1 \leq n \leq 100, 1 \leq a_{i,j},b_{i,j} \leq 10^4$

Algorithm

看见题目给了个 $\large C = \frac{\sum_{i = 1}^{n} a'_i}{\sum_{i = 1}^{n} b'_i}$ 的式子，阅题无数的同学一定就知道怎么做了：分数规划嘛。

题目要求最优化地安排一种方案，使得给定的描述方案性价比的比例式取得最值。

除非你能证明某种贪心策略的正确性，否则从正面考虑这样的问题是极端困难的。

01分数规划的思路则是从反面入手，我们二分答案。

我们二分最终的比值 $C$ ，如果存在某种方案的比值更优，则存在：

\[\begin{align*}
&\frac{\sum_{i = 1}^{n} a'_i}{\sum_{i = 1}^{n} b'_i} > C \\
\Rightarrow &\sum_{i = 1}^{n} a'_i > C \cdot \sum_{i = 1}^{n} b'_i \\
\Rightarrow &\sum_{i = 1}^{n} (C \cdot b'_i - a'_i) < 0
\end{align*}
\]

反之同理。

于是问题变成了不断验证是否存在 $\sum_{i = 1}^{n} (C \cdot b'_i - a'_i) > 0$ 继而不断缩小 $C$ 的可能取值范围。

换言之，如果我们实现了一个 $check(c)$ 函数能实现对应功能的话，就只需要这样写：

double l = 0, r = 1e6, mid;
while(r - l > eps)
{
    mid = (l + r) / 2;
    if(check(mid) < 0)	l = mid;
    else				r = mid;
}

我以为分数规划是一个令人心潮澎湃的算法。它既有理性的色彩，又极富暴力的美感，而且简单得惊人。

接下来考虑如何实现这个 $check(c)$ 。

先把题面上那个 $a'_i,b'_i$ 的一撇的扒掉。

现在问题本质上是给定一个矩阵 $c$ ，满足 $c_{i,j} = (C \cdot b_{i,j} - a_{i,j})$ ，

要求要在矩阵中选出 $n$ 个数字，满足不存在任意两个选中的数组在同一行或同一列。

怎么做呢？

我会暴力！$O(n!)$ 全排列！

……那还分数规划干啥
我会状压 DP ！用 $dp_{i,j}$ 表示现在考虑到第 $i$ 行，所有列是否已经取数的状态压缩成数字 $j$ 。

……复杂度 $O(n^2 \cdot 2^n \cdot log 1e6)$ ，大概能过 $40\%$ ？

我会费用流！

可以发现问题本质上是个男女匹配问题，于是考虑建立费用流模型。

考虑样例

\[a=\begin{bmatrix}
19 & 17 & 16 \\
25 & 24 & 23 \\
35 & 36 & 31 \\
\end{bmatrix}
,~~
b = \begin{bmatrix}
9 & 5 & 6 \\
3 & 4 & 2 \\
7 & 8 & 9 \\
\end{bmatrix}
\]

假如我们要验证 $C = 1$ 的情况，那么有

\[c = \begin{bmatrix}
10 & 12 & 10 \\
22 & 20 & 21 \\
28 & 28 & 22 \\
\end{bmatrix}
\]

建立这样一个图（本来想标注权值的，但是太糊了还是算了吧）：

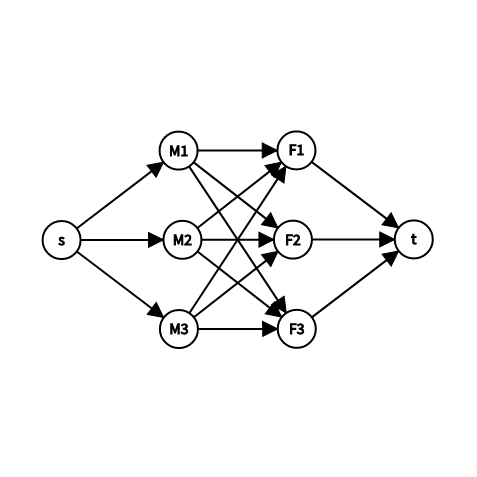
令图上所有边的流量上限都是 1 ，这就保证了最大流只能跑过图中的一些匹配。

令图中 $M_i \to F_j$ 的边权为 $c_{i,j}$ ，与 $s,t$ 连接的所有边权都为 0，那么我们需要验证的值就是跑最大流所经边权之和的最小值，也就是最小费用最大流。

有关最小费用最大流的实现，我是使用 $Dijkstra$ 配合势能函数魔改dinic的版本。

代码：

#include<bits/stdc++.h>
using namespace std;
const double eps = 1e-7;
template<const int N, const int M>
class Graph {
private:
	typedef pair<double, int> Node;
	priority_queue<Node> que;
	const double INF = 1e7;
	int beg[N], nex[M], tar[M], cap[M], ite[N], len;
	double pot[N], dis[N], cst[M];
	bool vis[N];
public:
	int n, s, t;
	inline void clear() {
		memset(pot, 0, sizeof(pot));
		memset(beg, 0, sizeof(beg));
		memset(nex, 0, sizeof(nex));
		len = 1;
	}
	Graph() {
		clear();
	}
	inline void add_edge(int a, int b, int c, double d)
	{
		++len, tar[len] = b, cap[len] = c, cst[len] = d;
		nex[len] = beg[a], beg[a] = len;
	}
	inline void add_pipe(int a, int b, int c, double d)
	{
		add_edge(a, b, c, +d);
		add_edge(b, a, 0, -d);
	}
	inline bool dijkstra(int s, int t)
	{
		fill(dis, dis + n + 1, INF);
		que.push(Node(dis[s] = 0, s));
		while(!que.empty())
		{
			Node cur = que.top();	que.pop();
			int u = cur.second;
			if(-cur.first > dis[u])	continue;
			for(int i = beg[u]; i; i = nex[i])
			{
				int v = tar[i];
				double tmp = dis[u] + cst[i] + pot[u] - pot[v];
				if(cap[i] && dis[v]- tmp > eps)
					que.push(Node(-(dis[v] = tmp), v));
			}
		}
		return dis[t] < INF;
	}
	int dfs(int u, int flo)
	{
		if(u == t)	return flo;
		int rst = flo;
		vis[u] = true;
		for(int &i = ite[u]; i; i = nex[i])
		{
			int v = tar[i];
			if(vis[v] || !cap[i])	continue;
			double tmp = dis[u] + cst[i] + pot[u] - pot[v];
			if(fabs(tmp - dis[v]) < eps)
			{
				int res = dfs(v, min(rst, cap[i]));
				rst -= res;
				cap[i] -= res;
				cap[i ^ 1] += res;
			}
		}
		vis[u] = false;
		return flo - rst;
	}
	inline Node costflow()
	{
		Node ret = Node(0, 0);
		while(dijkstra(s, t))
		{
			memcpy(ite, beg, sizeof(ite));
			int res = dfs(s, INF);
			for(int i = 1; i <= n; ++i)
				if(dis[i] < INF)	pot[i] += dis[i];
			ret.first += res * pot[t];
			ret.second += res;
		}
		return ret;
	}
};
template<class T>
inline void read(T &x)
{
	char c = getchar();	x = 0;
	while(c < '0' || '9' < c)	c = getchar();
	while('0' <= c && c <= '9')
	{
		x = (x << 1) + (x << 3) + c - 48;
		c = getchar();
	}
}
int n, a[128][128], b[128][128];
Graph<256, 32768> G;
double check(double c)
{
	G.clear();
	G.s = n + n + 2, G.n = G.t = G.s + 1;
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= n; ++j)
			G.add_pipe(i, j + n, 1, - a[i][j] + c * b[i][j]);
	for(int i = 1; i <= n; ++i)
	{
		G.add_pipe(G.s, i, 1, 0);
		G.add_pipe(i + n, G.t, 1, 0);
	}
	return G.costflow().first;
}
int main()
{
	read(n);
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= n; ++j)
			read(a[i][j]);
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= n; ++j)
			read(b[i][j]);
	double l = 0, r = 1e6, mid;
	while(r - l > eps)
	{
		mid = (l + r) / 2;
		if(check(mid) < 0)	l = mid;
		else				r = mid;
	}
	cout << fixed << setprecision(6) << mid << endl;
	return 0;
}