Leetcode（869）-重新排序得到 2 的幂

从正整数 N 开始，我们按任何顺序（包括原始顺序）将数字重新排序，注意其前导数字不能为零。

如果我们可以通过上述方式得到 2 的幂，返回 true；否则，返回 false。

示例 1：

输入：1
输出：true

示例 2：

输入：10
输出：false

示例 3：

输入：16
输出：true

示例 4：

输入：24
输出：false

思路：这个题的重点是求出数字的全排列（以0开头的除外），和数字是否2的幂

首先我们来总结下关于全排列。

这是一个c++函数，包含在头文件<algorithm>里面，下面是一般用法的基本格式。

1  int a[];
2  do{
3
4 }while(next_permutation(a,a+n));

STL提供了两个用来计算排列组合关系的函数，分别是next_permutation和prev_permutation。首先我们必须了解什么是“下一个”排列组合，什么是“前一个”排列组合。考虑三个字符所组成的序列{a,b,c}。这个序列有六个可能的排列组合：abc，acb，bac，bca，cab，cba。这些排列组合根据less-than操作符做字典顺序(lexicographical)的排序。也就是说，abc名列第一，因为每一个元素都小于其后的元素。acb是次一个排列组合，因为它是固定了a(序列内最小元素)之后所做的新组合。同样道理，那些固定b(序列中次小元素)而做的排列组合，在次序上将先于那些固定c而做的排列组合。以bac和bca为例，bac在bca之前，因为次序ac小于序列ca。面对bca，我们可以说其前一个排列组合是bac，而其后一个排列组合是cab。序列abc没有“前一个”排列组合，cba没有“后一个”排列组合。

所以一般在用next_permutation函数之前，都将数字排序好，按照从小到大的顺序。

下面来分析下next_permutation函数具体是怎么实现的。

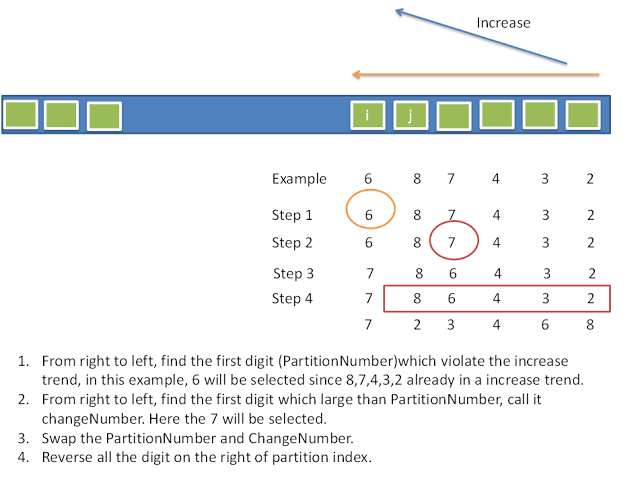
1. 从右往左扫描,发现第一个左邻小于右邻的数字,称之为 PartitionNumber, 如上图,6恰好是我们找到的 PartitionNumber .
2. 依然从右到左进行扫描,发现第一个比 PartitionNumber 要大的数,称之为 ChangeNumber.而7恰好是我们找到的 ChangeNumber ,需要注意的是,这样的数一定是存在的,否则的话,就找不到所以的 PartitionNumber 了.
3. 交换 PartitionNumber 和 ChangeNumber.这样一步,会使得新的排列组成的数比旧的排列组成的数要大,当然,新数增长的幅度不一定是最小的.
4. 交换之后，将当前ChangeNumber后面的数（或者原来PartitionNumber位置之后的数）从小到大排列一下,如此反转之后,可以保证,新的排列组成的数的增长幅度在所有的可能中最小.

 template<calss BidrectionalIterator>
 bool next_permutation(BidrectionalIterator first,BidrectionalIterator last)
 {
     if(first == last) return false; /* 空区间 */
     BidrectionalIterator i = first;
     ++i;
     if(i == last) return false;  /* 只有一个元素 */
     i = last;                    /* i指向尾端 */
     --i;
     for(;;)
     {
         BidrectionalIterator ii = i;
         --i;
         /* 以上锁定一组(两个)相邻元素 */
         if(*i < *ii)           /* 如果前一个元素小于后一个元素 */
         {
             BidrectionalIterator j = last; /* 令j指向尾端 */
             while(!(*i < *--j));     /* 由尾端往前找，直到遇到比*i大的元素 */
             iter_swap(i,j);          /* 交换i,j */
             reverse(ii,last);        /* 将ii之后的元素全部逆序重排 */
             return true;
         }
         if(i == first)       /* 进行至最前面了 */
         {
            reverse(first,last);    /* 全部逆序重排 */
             return false;
         }
     }
 }

接着我们讨论下，如何判断一个数是2的幂。

我们知道，1个数乘以2就是将该数左移1位，而2的0次幂为1， 所以2的n次幂（就是2的0次幂n次乘以2）就是将1左移n位， 这样我们知道如果一个数n是2的幂，则其只有首位为1，其后若干个0，必然有n & (n - 1)为0。（在求1个数的二进制表示中1的个数的时候说过，n&(n-1)去掉n的最后一个1）。因此，判断一个数n是否为2的幂，只需要判断n&(n-1)是否为0即可。

那如何判断是2的多少次方呢

int log2(int value)   //递归判断一个数是2的多少次方
{
 if (value == 1)
  return 0;
 else
  return 1+log2(value>>1);
}

下面附上本题的完整代码

 bool reorderedPowerOf2(int n)
 {
      int i,j,k,tmp;
      vector<int> a;
      a.clear();
      while (n>0)
      {
        a.push_back(n%10);
        n/=10;
      }
      sort(a.begin(),a.end());
      do
      {
        if (a[0]==0) continue;
        tmp=0;
        for (i=0;i<a.size();i++)
          tmp=tmp*10+a[i];
      if((tmp&tmp-1)==0)return true;
      }while (next_permutation(a.begin(),a.end()));
      return false;
    }