日照学习提高班day4测试

A

思路：

一看到这个题，他不仅要求输出字典序最小的串，还要满足两两不重复，所以我们可以先输出ababab...什么的，最后缀上要求的k-2种字母

坑点：

　　当然这样想是不完全的！该题是拥有许多特殊情况的！

　　例：

　　　　①当n==k的时候（直接从字符‘a’往后面一个一个接着输出就好啦~）

　　　　②除去①之后若k==1（即只允许一中字符出现，但是又需要输出多个字符的情况）（直接输出-1）

　　　　③当k>n的时候（直接输出-1）

　　　　④当k==2的时候（能输出多少对ab就输出几对ab，若不成对的话，倒数第二个输出a，即abababababababa什么的）

　　　　⑤当k==3的时候（最后输出‘c’，前面能输出几对ab就输出几对ab，若不成对的话，倒数第二个输出a，即abababababababa什么的）

　　　　⑥其余为普通情况（见思路）

上代码：

#include <iostream>
#include <cstdio>
using namespace std;

const int Maxn = ;
int n,k,cnt;
int p,p2;
//p是ab在不特殊情况下的总个数
//p2是在不特殊情况下除ab以外的总个数 

int main()
{
    freopen("str.in","r",stdin);
    freopen("str.out","w",stdout);
    scanf("%d%d",&n,&k);
    if(n==k) {
        for(int i=;i<n;++i)
            printf("%c",(char)i+'a');
        return ;
    }
    if(k== || k>n) {
        printf("-1");
        return ;
    }
    p=n-k+,p2=k-;
    bool flag=false;
    if(k<=) {
        while(cnt<n) {
            if(flag)
                printf("b"),flag=false;
            else
                printf("a"),flag=true;
            ++cnt;
        }
        return ;
    }
    if(k==) {
        while(cnt<n-) {
            if(flag)
                printf("b"),flag=false;
            else
                printf("a"),flag=true;
            ++cnt;
        }
        printf("c");
        return ;
    }
    while(cnt<p) {
        if(flag)
            printf("b"),flag=false;
        else
            printf("a"),flag=true;
        ++cnt;
    }
    for(int i=;i<+p2;++i)
        printf("%c",(char)i+);
    return ;
} 

---

B

思路:

　　①这是一道数论题，只需要根据排列组合推出来数学公式，然后用快速幂搞一搞即可（因为范围很大嘛~）

　　②在前k个点方案数的寻找中，也可以使用搜索

公式：

　　ans=ksm(k,k-1)%Mod * ksm(n-k,n-k)%Mod;

坑点:

一、我怎么知道这个公式啊啊啊!!!

所以需要手动推导一下!!!

①ksm(k,k-1)

• k==1的时候
• 只有一种情况：1 —> 1
• k==2的时候
• 只有2种情况：1 —> 2 ，2 —> 1
• k==3的时候
• 情况稍微多一点： 我们这里用一个表格来进行演示！
• 
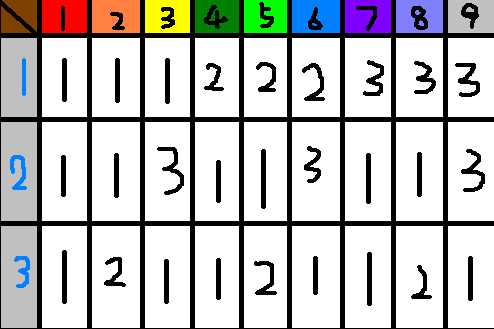
• 若还不懂，请自己手动实现一下吧还是。。。

②ksm(n-k,n-k)

• 因为题目中提到除那k个点之外，其他点不能够连到1，而又因为k个点每个点都必须能够走到1，这即是说明后n-k个点不能够连到k个点，所以他们能够胡乱连，只要不到k个点即可，
• 所以方案数为ksm(n-k,n-k);
• （因为每个点都有n-k种选择）

③至于为什么要%Mod

• 对此我只能说：题目要求。。。。

二、在搜索的时候数组一定不要开到8就算了，会T掉....

所以要开到9！！

看似数据中存在k==9的情况qwq ，因为我开到8后T了3个点，但是多加了一个之后就A了。。。

上代码:

• 数论版:

#include <iostream>
#include <cstdio>
#define LL long long
using namespace std;

const int Mod = 1e9 + ;
LL n,k,ans;

inline LL read(LL &AC)
{
    char ch=' ';LL x=,f=;
    for(; (ch!='-') && ((ch<'')||(ch>'')); ch=getchar());
    if(ch=='-') f=-,ch=getchar();
    for(; ch>='' && ch<=''; ch=getchar()) x=x*+ch-;
    AC=x*f;    return AC;
}

inline LL ksm(LL a,LL p) {
    LL ret = ;
    a%=Mod;
    for(; p; p>>=, a=a*a%Mod)
        if(p&)
            ret=ret*a%Mod;
    return ret;
}

int main() {
    read(n),read(k);
    ans=ksm(k,k-)%Mod*ksm(n-k,n-k)%Mod;
    printf("%lld",ans);
    return ;
}

• 搜索版:

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#define LL long long
using namespace std;

const int Mod = 1e9 + ;
const int Maxk = ;
LL n,k,ans;
int pi[Maxk];

inline LL read(LL &AC)
{
    char ch=' ';LL x=,f=;
    for(; (ch!='-') && ((ch<'')||(ch>'')); ch=getchar());
    if(ch=='-') f=-,ch=getchar();
    for(; ch>='' && ch<=''; ch=getchar()) x=x*+ch-;
    AC=x*f;    return AC;
}

inline LL ksm(LL a,LL p) {
    LL ret = ;
    a%=Mod;
    for(; p; p>>=, a=a*a%Mod)
        if(p&)
            ret=ret*a%Mod;
    return ret;
}

inline bool check() {
    bool vis[Maxk];
    memset(vis,false,sizeof(vis));
    int now=;
    while(!vis[now]) {
        vis[now]=true;
        now=pi[now];
    }
    ///从 1 出发必须能够回到 1
    if(now!=)
        return false;
    for(int i=; i<=k; ++i) {
        if(!vis[i]) {
            bool vis2[Maxk];
            memset(vis2,false,sizeof(vis2));
            int now2=i;
            while(!vis2[now2] && !vis[now2]) {
                vis2[now2]=true;
                now2=pi[now2];
            }
            if(!vis[now2])
                return false;
        }
    }
    return true;
}

void dfs(int now) {
    if(now==k+) {
        if(check())
            ans++;
        return ;
    }
    for(int i=; i<=k; ++i) {
        pi[now]=i;
        dfs(now+);
    }
}

int main() {
    read(n),read(k);
    dfs();
    ans=ans*ksm(n-k,n-k)%Mod;
    printf("%lld",ans);
    return ;
}

---

C

思路:

这题需要优化的dp！！！

　　但是为什么可以优化那？

　　首先时间上的优化：

　　　　因为每一次递推改变的是一个范围内的值，所以能用差值维护。

　　其次空间上的优化：

　　　　每一步仅与他的上一步有关，能用滚动数组。

坑点:

最后ans记录的时候用的是last,不是now，因为最后有一次互换操作！

上代码:

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#define LL long long
using namespace std;

const int Maxn = ;
const int Mod = 1e9 + ;
int n,a,b,k;
///滚动数组 ,二维是代表终点在第几层
LL dp[][Maxn];
///up代表第i层能走到的最上方的层数为...,down反之
int up[Maxn],down[Maxn];

int main() {
    freopen("lift.in","r",stdin);
    freopen("lift.out","w",stdout);
    scanf("%d%d%d%d",&n,&a,&b,&k);
    int last=,now=;
    ///初始化:自己从a出发到a的方法只有1种
    dp[last][a]=;
    for(int i=; i<=n; ++i) {
        ///处理每一层到达b的距离
        int dis=abs(i-b);
        /*
        1-n是从上到下,所以i-dis+1要比i+dis-1要小,所以i-dis+1在上方
        见图示
        又因为i可能减不了,但是up又不能够<1,所以在i-dis+1跟1中取max
        down同理
        */
        up[i]=max(,i-dis+);
        down[i]=min(n,i+dis-);
    }
    for(int i=; i<=k; ++i) {
        ///使用滚动数组要先将将要更新的清零
        for(int j=; j<=n; ++j)
            dp[now][j]=;
        for(int j=; j<=n; ++j) {
            (dp[now][up[j]]+=dp[last][j])%Mod;
            (dp[now][down[j]+]-=dp[last][j])%Mod;
        }
        ///处理前缀和
        for(int j=; j<=n; ++j)
            (dp[now][j]+=dp[now][j-])%Mod;
        ///滚动数组(处理完前缀和之后,上一个就已经没用了,减去)
        for(int j=; j<=n; ++j)
            (dp[now][j]-=dp[last][j])%Mod;
        ///进行交换
        swap(last,now);
    }
    int ans=;
    /*
    为什么用last不用now呢?
    因为上一个for循环中最后结束的时候又把last跟now换了
    所以本来最后i==k时now代表k,换完之后变为last
    */
    ///因为每一层都有可能是终点,ans都累加一遍即可
    for(int i=; i<=n; ++i)
        (ans+=dp[last][i])%Mod;
    ///防止出现负数
    ans=(ans+Mod)%Mod;
    cout<<ans;
    return ;
}