用matlab脚本语言写M文件函数时用三种方法简单实现实现DFT（离散傅里叶变换）

%用二重循环实现DFT：
function xk=dt_0(xn);     %define a function
N=length(xn);           %caculate the length of the variable
WN=exp(-j.*.*pi./N);
xk=zeros(,N);          %define a non-zero 一维矩阵
sum=zeros(,N);          %define a non-zero 一维矩阵
for k=:N            %二重循环实现离散傅里叶变换DFT

    for n=:N

       sum(n)=xn(n).*WN.^(k.*n);
       xk(k)=xk(k)+sum(n);

    end         

end
end

%用一重循环和内积实现DFT：
function xk=dt_1(xn);

 N=length(xn);
 WN=exp(-j.*.*pi./N);
 xk=zeros(,N);
  n=[:N-];
 for k=::N-;
   xk(k+)=xn*WN.^(k.*n');  %此处下标一定得从1开始，因为matlab的下标是从1开始的

 end    

end

%不用循环，仅有内积相乘实现DFT：
function xk=dt_2(xn);
N=length(xn);

WN=exp(-j**pi/N);
n=::N-;     %定义一个一维矩阵，即行向量,从0到N-
k=::N-;
nk=k'*n;      %行向量k变换为列向量 乘上 行向量n ，得到一个N x N的矩阵
WNnk=WN.^(nk);      %做幂运算后的参数仍为一个 N x N的系数矩阵
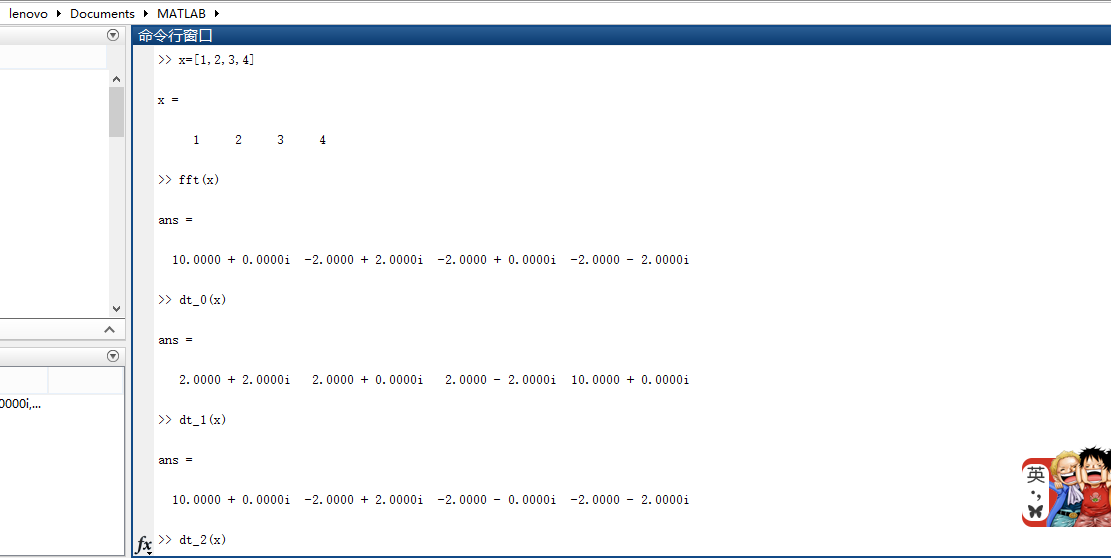
xk=xn*WNnk;       %行向量 乘以  N x N的系数矩阵 即为DFT变换后的矩阵

end

以下是输入一个行向量xn=[1,2,3,4]，MATLAB中用以上三种方法进行DFT的结果如下图所示：