[CSP-S模拟测试]:跳房子（模拟）

题目描述

跳房子，是一种世界性的儿童游戏，也是中国民间传统的体育游戏之一。
跳房子是在$N$个格子上进行的，$CYJ$对游戏进行了改进，该成了跳棋盘，改进后的游戏是在一个$N$行$M$列的棋盘上进行，并规定从第一行往上可以走到最后一行，第一列往左可以走到最后一列，反之亦然。每个格子上有一个数字。
在这个棋盘左上角$(1,1)$放置着一枚棋子。每次棋子会走到右、右上和右下三个方向格子中对应上数字最大一个。即任意时刻棋子都只有一种走法，不存在多个格子同时满足条件。
现在有两种操作：
$move\ k$将棋子前进$k$步。
$change\ a\ b\ e$将第$a$行第$b$列格子上的数字修改为$e$。
请对于每一个$move$操作输出棋子移动完毕后所处的位置。

---

输入格式

第一行包含两个正整数$N,M$，表示棋盘的大小。
接下来$N$行，每行$M$个整数，依次表示每个格子中的数字$a[i,j]$。
接下来一行包含一个正整数$Q$，表示操作次数。
接下来$m$行，每行一个操作。

---

输出格式

对于每个$move$操作，输出一行两个正整数$x,y$，即棋子所处的行号和列号。

---

样例

样例输入

4 4
1 2 9 3
3 5 4 8
4 3 2 7
5 8 1 6
4
move 1
move 1
change 1 4 100
move 1

样例输出

4 2
1 3
1 4

---

数据范围与提示

$10\%$的数据满足：$3\leqslant N,M\leqslant 50$，$Q\leqslant 5,000$，$k\leqslant 50$；
$20\%$的数据满足：$3\leqslant N,M\leqslant 200$，$Q\leqslant 5,000$，$k\leqslant 5,000$；
另有$20\%$的数据满足：$3\leqslant N,M\leqslant 200$，$Q\leqslant 5,000$，$k\leqslant {10}^9$；
$100\%$的数据满足：$3\leqslant N,M\leqslant 2,000$，$Q\leqslant 5,000$，$e,k\leqslant {10}^9$；

---

题解

$30\%$算法：

暴力模拟，注意边界问题，可以考虑将整张图向左上移一位，也就是说原来的$(1,1)$现在是$(0,0)$。

时间复杂度：$\Theta(k\times Q)$。

期望得分：$30$分。

$50\%$算法：

发现$k$巨大，所以我们考虑从$k$入手。

惊喜的发现，在走了一定的步数之后会出现循环，那么我们可以计算出这个循环的大小，然后直接用剩下的步数$mod$循环的大小即可。

注意$change$的时候清空循环标记的时候不要用$memset$，否则时间复杂度会退化。

时间复杂度：$\Theta(N^2\times Q)$。

期望得分：$50$分。

$100\%$算法：

正解似乎是线段树$+$置换$+$快速幂，我瞎搞了一个。

时间复杂度：$\Theta(Q\times N\log M)$。

期望得分：$100$分。

但是我还是挺晕的，所以我打了个大模拟，跑的比正解快（理论时间复杂度也比正解小）。

还是从$k$入手，开一个数组$jump[i]$表示从第一列的第$i$行开始，再走到第一列会走到哪一行。

预处理出来上面的那个数组，然后我们可以利用基环树的思想找环，并且记录环长，和哪些点在环上。

至于$move$，分三步走：

　$alpha.$先让它暴力往前走到第一列。

　$beta.$疯狂的跳，跳到环里直接$mod$环的大小，然后再疯狂的跳，直到剩余步数$<M$为止。

　$\gamma.$把剩下的步数暴力走完即可。

至于$change$，就显得麻烦多了：

　$alpha.$我们要注意到，$change$了点$(i,j)$，会影响的只有$(i-1,j-1)，(i,j-1)，(i+1,j-1)$，那么这时候这三个点还分三种情况：

　　

　　$\mathcal{a}.$原来走点$(i,j)$现在还走点$(i,j)$，那么不用管他。

　　$\mathcal{b}.$原来走点$(i,j)$但是现在不走点$(i,j)$，那么我们就要看这个点现在能走到第一列的哪个点，然后在看第一列中的那些点可以走到它，更改这些点的$jump$值即可。

　　$\mathcal{c}.$原来不走点$(i,j)$但是现在走点$(i,j)$，那么我们看点$(i,j)$能走到第一列中的哪个点，然后看第一列中的哪些点可以走向它，更改这些点的$jump$值即可。

　$beta.$显然上面的方法不优，理论上讲最劣的情况下每更改一个点会遍历半张图，也就是$2,000,000$个点，还有$5,000$次询问，显然是不能接受的，最多能够拿到$80$分。

　　那么开始考虑优化，我们会发现，下面这种情况一定不会发生：

　　

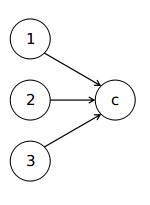
　　因为点$1$走向点$4$也就意味着点$4$的权值大于点$2$那么点$3$一定会走向点$4$而不是点$2$，转而言之，路径肯定不会交叉。

　　现在我们就找到了优化的方式，我们可以只找第一列中受影响的最上面的那一个点和最下面的那一个点，然后它们之间所有的点都是受影响的点。

　　如下图所示，我们只用从红边走回去，黑边不用走，找到上界点$1$和下界点$4$，所以点$1,2,3,4$都受影响，然而点$5$不受影响。

　　

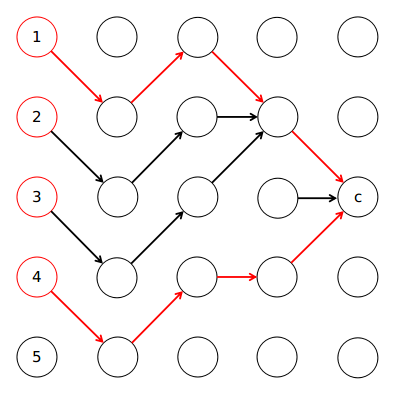
　　需要注意一些细节，你可能会发现球出来的上界比下界还大，这是为什么呢？

　　如下图：

　　

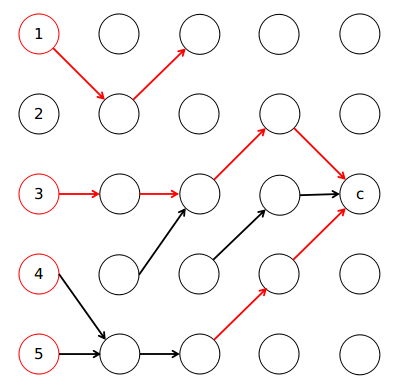
　　也就是说在往回找的过程中越过了边界，那么我们需要更改的区间是两侧，但是你可能有疑问，为什么不能包含整个区间呢？

　　

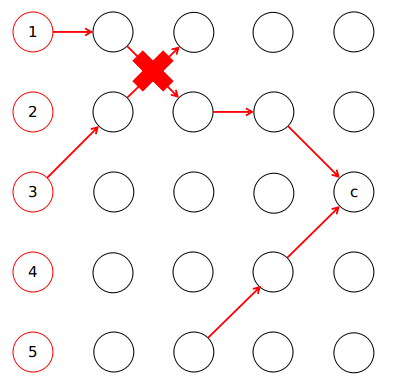
　　显然这时候会出现上面所说的交叉情况，所以这种情况一定不会发生，放心搞就好了。

时间复杂度：$\Theta(M\times Q)$（比正解还低）。

期望得分：$100$分。

---

代码时刻

$50\%$算法：

#include<bits/stdc++.h>
using namespace std;
int n,m,q;
int x,y;
int Map[2000][2000];
int vis[2000][2000];
int cnt;
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
			scanf("%d",&Map[i][j]);
	scanf("%d",&q);
	while(q--)
	{
		char opt[10];
		scanf("%s",opt+1);
		if(opt[1]=='m')
		{
			int k;
			scanf("%d",&k);
			while(k--)
			{
				int xu=(x-1+n)%n,xd=(x+1)%n,ny=(y+1)%m;
				int nowa=Map[xu][ny];
				int nowb=Map[x ][ny];
				int nowc=Map[xd][ny];
				if(nowa>nowb&&nowa>nowc)
				{
					cnt++;
					x=xu;
					y=ny;
				}
				else if(nowb>nowa&&nowb>nowc)
				{
					cnt++;
					y=ny;
				}
				else
				{
					cnt++;
					x=xd;
					y=ny;
				}
				if(vis[x][y])k=k%(cnt-vis[x][y]);
				vis[x][y]=cnt;
			}
			printf("%d %d\n",x+1,y+1);
		}
		else
		{
			int a,b,e;
			scanf("%d%d%d",&a,&b,&e);
			Map[a-1][b-1]=e;
			for(int i=0;i<n;i++)
				for(int j=0;j<m;j++)
					vis[i][j]=0;
			cnt=0;
		}
	}
	return 0;
}

$100\%$算法（模拟）：

#include<bits/stdc++.h>
using namespace std;
#define register
int n,m,q;
int Map[2000][2000],vis[2000],sta[2000],insta[2000],is_c[2000],jump[2000],num;
int nowx,nowy;
int nxtstep(int x,int y)
{
	int xup=(x-1+n)%n,xdown=(x+1+n)%n;
	if(y==m-1)return Map[x][0]>Map[xup][0]?(Map[x][0]>Map[xdown][0]?x:xdown):(Map[xup][0]>Map[xdown][0]?xup:xdown);
	return Map[x][y+1]>Map[xup][y+1]?(Map[x][y+1]>Map[xdown][y+1]?nxtstep(x,y+1):nxtstep(xdown,y+1)):(Map[xup][y+1]>Map[xdown][y+1]?nxtstep(xup,y+1):nxtstep(xdown,y+1));
}
void move(int k)
{
	while(nowy&&k)
	{
		k--;
		nowy=(nowy+1)%m;
		int xup=(nowx-1+n)%n,xdown=(nowx+1+n)%n;
		if(Map[nowx][nowy]>Map[xup][nowy]&&Map[nowx][nowy]>Map[xdown][nowy])nowx=nowx;
		else if(Map[xup][nowy]>Map[nowx][nowy]&&Map[xup][nowy]>Map[xdown][nowy])nowx=xup;
		else if(Map[xdown][nowy]>Map[nowx][nowy]&&Map[xdown][nowy]>Map[xup][nowy])nowx=xdown;
	}
	while(!is_c[nowx]&&k>=m)
	{
		k-=m;
		nowx=jump[nowx];
	}
	k%=num;
	while(k>=m)
	{
		k-=m;
		nowx=jump[nowx];
	}
	while(k)
	{
		k--;
		nowy=(nowy+1)%m;
		int xup=(nowx-1+n)%n,xdown=(nowx+1+n)%n;
		if(Map[nowx][nowy]>Map[xup][nowy]&&Map[nowx][nowy]>Map[xdown][nowy])nowx=nowx;
		else if(Map[xup][nowy]>Map[nowx][nowy]&&Map[xup][nowy]>Map[xdown][nowy])nowx=xup;
		else if(Map[xdown][nowy]>Map[nowx][nowy]&&Map[xdown][nowy]>Map[xup][nowy])nowx=xdown;
	}
}
void judge(int x)
{
	vis[x]=insta[x]=1;
	sta[++sta[0]]=x;
	if(insta[jump[x]])
	{
		int y;
		num=0;
		do
		{
			y=sta[sta[0]--];
			insta[y]=0;
			is_c[y]=1;
			num+=m;
		}while(y!=jump[x]);
	}
	else if(!vis[jump[x]])judge(jump[x]);
	insta[x]=0;
}
int updatel(int x,int y)
{
    if(y==0)return x;
    int xu1=(x-1+n)%n,xd1=(x+1+n)%n;
	int xu2=(xu1-1+n)%n,xd2=(xd1+1+n)%n;
	int l=-1;
    if(l==-1&&Map[x][y]>Map[xu1][y]&&Map[x][y]>Map[xu2][y])l=updatel(xu1,y-1);
    if(l==-1&&Map[x][y]>Map[xu1][y]&&Map[x][y]>Map[xd1][y])l=updatel(x  ,y-1);
    if(l==-1&&Map[x][y]>Map[xd1][y]&&Map[x][y]>Map[xd2][y])l=updatel(xd1,y-1);
    return l;
}
int updater(int x,int y)
{
    if(y==0)return x;
    int xu1=(x-1+n)%n,xd1=(x+1+n)%n;
	int xu2=(xu1-1+n)%n,xd2=(xd1+1+n)%n;
	int r=-1;
	if(r==-1&&Map[x][y]>Map[xd1][y]&&Map[x][y]>Map[xd2][y])r=updater(xd1,y-1);
	if(r==-1&&Map[x][y]>Map[xu1][y]&&Map[x][y]>Map[xd1][y])r=updater(x  ,y-1);
	if(r==-1&&Map[x][y]>Map[xu1][y]&&Map[x][y]>Map[xu2][y])r=updater(xu1,y-1);
	return r;
}
void update(int x,int y,int to)
{
    if(y==0)
    {
        jump[x]=to;
        return;
    }
	int xu1=(x-1+n)%n,xd1=(x+1+n)%n;
	int xu2=(xu1-1+n)%n,xd2=(xd1+1+n)%n;
	int l=-1,r=-1;
	if(Map[x][y]>Map[xu1][y]&&Map[x][y]>Map[xu2][y]&&l==-1)l=updatel(xu1,y-1);
	if(Map[x][y]>Map[xu1][y]&&Map[x][y]>Map[xd1][y]&&l==-1)l=updatel(x,y-1);
	if(Map[x][y]>Map[xd1][y]&&Map[x][y]>Map[xd2][y]&&l==-1)l=updatel(xd1,y-1);
    if(Map[x][y]>Map[xd1][y]&&Map[x][y]>Map[xd2][y]&&r==-1)r=updater(xd1,y-1);
	if(Map[x][y]>Map[xu1][y]&&Map[x][y]>Map[xd1][y]&&r==-1)r=updater(x,y-1);
    if(Map[x][y]>Map[xu1][y]&&Map[x][y]>Map[xu2][y]&&r==-1)r=updater(xu1,y-1);
	if(l==-1)return;
	if(l>r)
	{
	    for(int i=l;i<n;i++)jump[i]=to;
	    for(int i=0;i<=r;i++)jump[i]=to;
	}
	for(int i=l;i<=r;i++)jump[i]=to;
}
void change(int x,int y,int e)
{
	int xu1=(x-1+n)%n,xd1=(x+1+n)%n;
	int xu2=(xu1-1+n)%n,xd2=(xd1+1+n)%n;
	int ny=(y-1+m)%m;
	int tu1,tu2,td1,td2,to;
	if(y)
	{
		to=nxtstep(x,y);
	    tu1=nxtstep(xu1,y);
	    tu2=nxtstep(xu2,y);
	    td1=nxtstep(xd1,y);
	    td2=nxtstep(xd2,y);
	}
	else
	{
		to=x;
	    tu1=xu1,tu2=xu2;
	    td1=xd1,td2=xd2;
	}
	if((Map[xu1][y]>Map[x][y]||Map[xu2][y]>Map[x][y])&& e>Map[xu1][y]&&e>Map[xu2][y] )update(xu1,ny,to                             );
	if( Map[xu1][y]<Map[x][y]&&Map[xu2][y]<Map[x][y] &&(e<Map[xu1][y]||e<Map[xu2][y]))update(xu1,ny,Map[xu1][y]>Map[xu2][y]?tu1:tu2);
	if((Map[xu1][y]>Map[x][y]||Map[xd1][y]>Map[x][y])&& e>Map[xu1][y]&&e>Map[xd1][y] )update(x  ,ny,to                             );
	if( Map[xu1][y]<Map[x][y]&&Map[xd1][y]<Map[x][y] &&(e<Map[xu1][y]||e<Map[xd1][y]))update(x  ,ny,Map[xu1][y]>Map[xd1][y]?tu1:td1);
	if((Map[xd1][y]>Map[x][y]||Map[xd2][y]>Map[x][y])&& e>Map[xd1][y]&&e>Map[xd2][y] )update(xd1,ny,to                             );
	if( Map[xd1][y]<Map[x][y]&&Map[xd2][y]<Map[x][y] &&(e<Map[xd1][y]||e<Map[xd2][y]))update(xd1,ny,Map[xd1][y]>Map[xd2][y]?td1:td2);
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
			scanf("%d",&Map[i][j]);
	for(int i=0;i<n;i++)
		jump[i]=nxtstep(i,0);
	for(int i=0;i<n;i++)
		if(!vis[i])judge(i);
	scanf("%d",&q);
	while(q--)
	{
		char opt[10];
		scanf("%s",opt);
		if(opt[0]=='m')
		{
			int k;
			scanf("%d",&k);
			move(k);
			printf("%d %d\n",nowx+1,nowy+1);
		}
		else
		{
			int a,b,e;
			scanf("%d%d%d",&a,&b,&e);
			a--,b--;
			change(a,b,e);
			Map[a][b]=e;
			for(int i=0;i<n;i++)vis[i]=is_c[i]=0;
			sta[0]=0;
			for(int i=0;i<n;i++)
				if(!vis[i])judge(i);
		}
	}
}

$100\%$算法（正解）：

#include<bits/stdc++.h>
#define L(x) x<<1
#define R(x) x<<1|1
using namespace std;
int n,m,q;
struct rec{int nxt[2001];rec(){for(int i=1;i<=n;i++)nxt[i]=i;}}t[2001],tr[8001];
int Map[2001][2001];
int nxt[2001][2001];
int nowx=1,nowy=1;
int modd(int x,bool flag)
{
	if(x==(flag?m+1:n+1))return 1;
	if(!x)return flag?m:n;
	return x;
}
void change(int x,int y)
{
	x=modd(x,0);
	y=modd(y,1);
	int nxty=modd(y+1,1);
	int x_1=modd(x-1,0);
	int x_2=modd(x,0);
	int x_3=modd(x+1,0);
	int maxn=Map[x_1][nxty];
	t[y].nxt[x]=x_1;
	if(maxn<Map[x_2][nxty])
	{
		maxn=Map[x_2][nxty];
		t[y].nxt[x]=x_2;
	}
	if(maxn<Map[x_3][nxty])
	{
		maxn=Map[x_3][nxty];
		t[y].nxt[x]=x_3;
	}
}
void pushup(int x)
{
	for(int i=1;i<=n;i++)
		tr[x].nxt[i]=tr[R(x)].nxt[tr[L(x)].nxt[i]];
}
void build(int x,int l,int r)
{
	if(l==r)
	{
		tr[x]=t[l];
		return;
	}
	int mid=(l+r)>>1;
	build(L(x),l,mid);
	build(R(x),mid+1,r);
	pushup(x);
}
void move(int k){while(k--){nowx=t[nowy].nxt[nowx];nowy=modd(nowy+1,1);}}
rec qpow(rec x,int y)
{
	rec res;
	while(y)
	{
		if(y&1)
			for(int i=1;i<=n;i++)
				res.nxt[i]=x.nxt[res.nxt[i]];
		rec flag;
		for(int i=1;i<=n;i++)
			flag.nxt[i]=x.nxt[x.nxt[i]];
		x=flag;
		y>>=1;
	}
	return res;
}
void update(int x,int l,int r,int w)
{
	if(l==r)
	{
		tr[x]=t[w];
		return;
	}
	int mid=(l+r)>>1;
	if(w<=mid)update(L(x),l,mid,w);
	else update(R(x),mid+1,r,w);
	pushup(x);
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%d",&Map[i][j]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			change(i,j);
	build(1,1,m);
	scanf("%d",&q);
	while(q--)
	{
		char opt[10];
		scanf("%s",opt+1);
		if(opt[1]=='m')
		{
			int k;
			scanf("%d",&k);
			int len=min(k,m-nowy+1);
			move(len);
			k-=len;
			if(k){nowx=qpow(tr[1],k/m).nxt[nowx];k%=m;move(k);}
			printf("%d %d\n",nowx,nowy);
		}
		else
		{
			int a,b,e;
			scanf("%d%d%d",&a,&b,&e);
			Map[a][b]=e;
			change(a-1,b-1);
			change(a,b-1);
			change(a+1,b-1);
			update(1,1,m,modd(b-1,1));
		}
	}
	return 0;
}

---

rp++