EM 算法(一)-原理

讲到 EM 算法就不得不提极大似然估计，我之前讲过，请参考我的博客

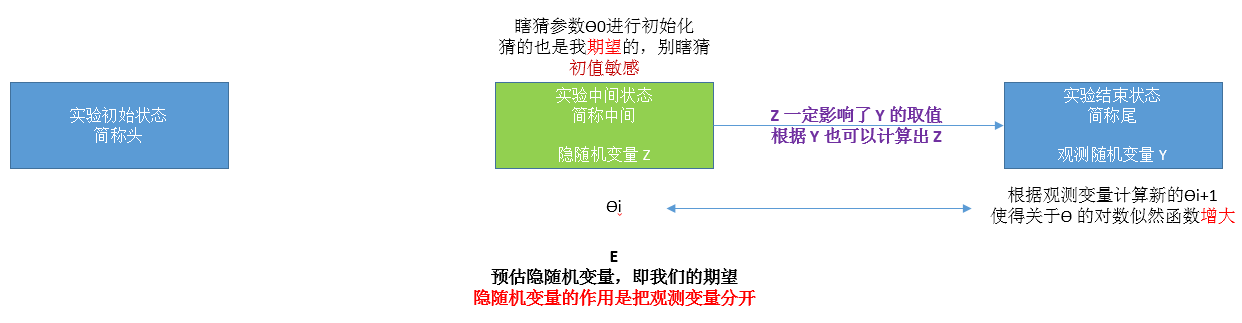
下面我用一张图解释极大似然估计和 EM 算法的区别

EM 算法引例1-抛3枚硬币

还是上图中抛硬币的例子，假设最后结果正面记为1，反面记为0，抛10次，结果为 1101001011；

下面我用数据公式解释下这个例子和 EM 算法；

三硬币模型可以写作

θ 表示模型参数，即三枚硬币正面的概率，用 π p q 表示；

y 表示观测随机变量，取值为 0,1；

z 表示隐随机变量，在本例中就是 A 的正反面，或者是选择 B 还是不选择 B；

P(y|θ) 表示该参数下，y 出现的概率；

剩下的不多解释，很容易理解

将观测变量表示为 Y=(Y1,Y2...YN)，将隐变量表示为 Z=(Z1,Z2...ZN)，则观测变量的似然函数为

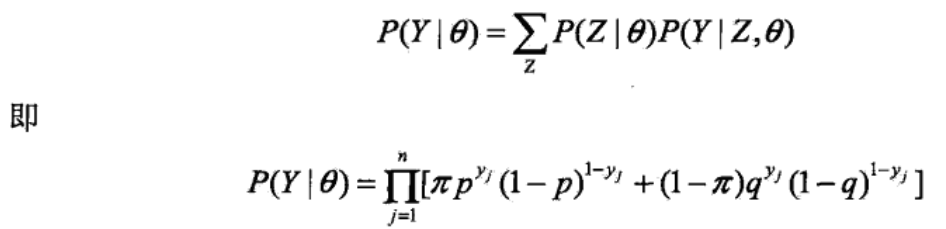n 是实验次数

连乘取 log，转换成 θ 的对数似然函数

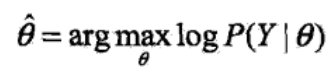
这个式子是问题的本质，但是它没有解析解，只能通过迭代求解

EM 算法就是一种迭代的算法

迭代首先要有个初值，即 θ 的初始化

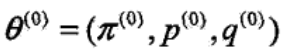
假设我们已经迭代了 i 次，获得新的 θ

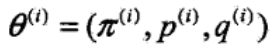
接下来要求 i+1 次的 θ　　　　　　【这里就是要建立迭代关系，很重要的一步】

重点是得到隐随机变量的期望，根据 θⁱ 得到第 i+1 次 B 出现的概率

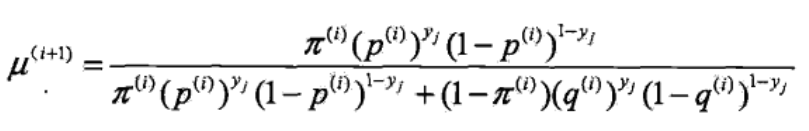　　【B/B+C】

上式用概率表示为 P(B|y,θ) ，也就是在参数为 θ 时，基于 y 计算 B 的概率　　　　【上式是李航教材里这么写的，个人认为应该是把所有观测变量带入该式子，然后求平均，也就是 B 的期望】

这是 B 出现的概率，也就是预估，或者说期望，Exception，也就是 EM 的 E 步

1-uⁱ⁺¹ 也就是 C 出现的概率；

然后就可以根据观测变量，重新计算 θ

π 代表 A 出现正面的概率，等价于隐随机变量是 B 的概率，实验 n 次，求均值即可

p 代表 B 出现正面的概率，即隐变量是 B，然后观测变量是 1

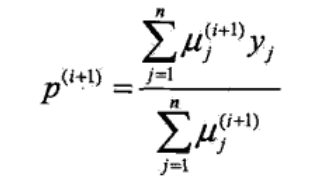
q 代表 C 出现正面的概率，即隐变量是 C，然后观测变量是 1

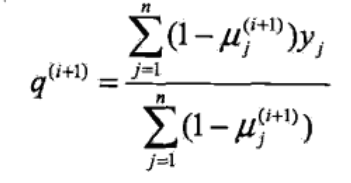
似然函数解析

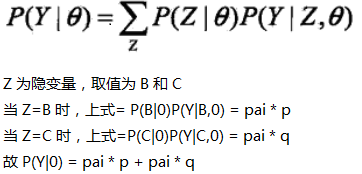
这一步使得 θ 的对数似然函数更大，即 EM 的 M 步，max

有了新的 θ，继续迭代即可，直至 θ 不变或者 θⁱ⁺¹-θⁱ<阈值，停止迭代

笔者展示了如下迭代

我想强调的是初值对结果有影响，也就是 EM 算法对初值敏感

小结

EM 算法引例2-抛2枚硬币

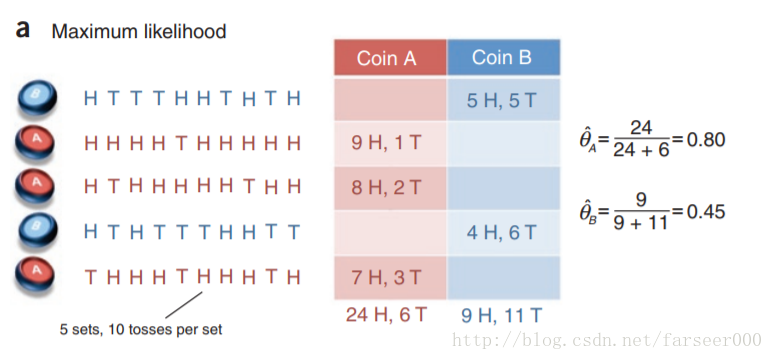
有两枚硬币 A B，每次从两枚硬币中随机取一个，抛 10 次，记录每次正反面，总共取 5 次，也就是抛 50 次；

目标是预测 A B 各自正面朝上的概率

抛开这个问题，我们考虑一下，随便拿个硬币，抛100次，正面出现60次，反面出现40次，那这枚硬币正面朝上的概率岂不就是 0.6，是的，然后回到我们的实验

极大似然

假如我们知道每次取得是 A 还是 B，那就没有隐变量，转换成极大似然问题，很简单；

EM

现在我们不知道取出来的是 A 还是 B，就有了隐变量，转换成 EM 问题

EM 算法

由以上两个例子，我们引出 EM 算法的具体描述

EM 算法的收敛

EM算法是可以正面收敛性的，后续在补充吧，毕竟麻烦

参考资料：

https://zhuanlan.zhihu.com/p/36331115　　人人都懂EM算法

https://www.zhihu.com/question/40797593/answer/275171156

https://zhuanlan.zhihu.com/p/78311644

https://zhuanlan.zhihu.com/p/60376311　　猴子也能理解的EM算法

https://blog.csdn.net/u014157632/article/details/65442165

《统计学习方法》　李航

《机器学习》周志华