BZOJ 4017 小 Q 的无敌异或 ( 树状数组、区间异或和、区间异或和之和、按位计贡献思想 )

题目链接

题意 : 中文题

分析 :

首先引入两篇写的很好的题解

题解一、题解二

听说这种和异或相关区间求和的问题都尽量按位考虑

首先第一问、按二进制位计贡献的话、那么对于第 k 位而言

其贡献 = 区间异或和第 k 位为 1 的子区间个数 * 2^k

而能产生贡献的子区间必定满足 xorSum(R) ^ xorSum(L-1) 第 k 位为 1

注 : xorSum 为前缀异或和

要快速计算这个东西其实很简单、先计算出 xorSum

然后枚举右端点 R 、累计到目前为止每个位的 0 和 1 的数量

就能做到 O(1) 转移

假设 xorSum(R) 的第 k 位为 0

那么其贡献就应该为前面所有累计的 1 的数量  * 2^k

第二问就稍许复杂了些、但大体思路也是使用按位计贡献的思路

如果一个区间的所有子区间之和的第 k 位为 1 的话、那么所有子区间的和

在第 k 位上为 1 的子区间个数应当为奇数

也就是说 PreSum(R) - PreSum(L-1) 第 k 位为 1、这样子的二元组 (L、R) 有奇数个

注 : PreSum(i) 为前缀和

“PreSum(R) - PreSum(L-1) 第 k 位为 1”

这句话可以用一个不等式来表示

( PreSum(R) - PreSum(L-1) ) mod (2^(k+1)) ≥ 2^k

( 假设最后一位为第 0 位、即 k 从 0 开始算 )

原理可以这样子思考、你想你在十进制下截取一个数的后 k 位用什么办法？

是不是直接 mod 10^(k+1) ( 假设最后一位为第 0 位 )

二进制下也是一样的道理

不过模数涉及到减法就可能产生负数、需要对结果另加模数

那么对上述式子进行变形、有两种满足条件

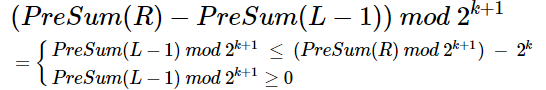
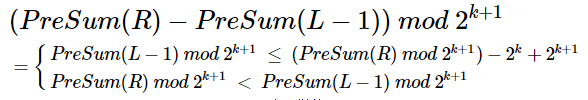
可以发现如果枚举右端点的话、那么就是统计满足条件的 PreSum(L-1) mod 2^(k+1) 的个数了

那么由于是不等关系、那么可以先离散化所有的 PreSum(L-1) mod 2^(k+1) 值

存进去树状数组中便可轻易统计数量

不过与其算出数量再来判断奇偶、官方题解给出了更为巧妙的实现方法

也是用到了异或的性质、把树状数组存的值变成前缀异或和

那么如果查询的异或和是 1 那么说明是奇数、否则是偶数、可以看程序去体会一下

有一点要注意、就是离散的值都是 PreSum[i] mod 2^(k+1)

所以在二分查找的时候、可能不会在离散化后的数组里面找到相对应的值

那么要将它的贡献放入树状数组当中的话就要二分查找出一个 ≤ 它的位置、然后去异或 1

#include<bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
 
#define scl(i) scanf("%lld", &i)
#define scll(i, j) scanf("%lld %lld", &i, &j)
#define sclll(i, j, k) scanf("%lld %lld %lld", &i, &j, &k)
#define scllll(i, j, k, l) scanf("%lld %lld %lld %lld", &i, &j, &k, &l)
 
#define scs(i) scanf("%s", i)
#define sci(i) scanf("%d", &i)
#define scd(i) scanf("%lf", &i)
#define scIl(i) scanf("%I64d", &i)
#define scii(i, j) scanf("%d %d", &i, &j)
#define scdd(i, j) scanf("%lf %lf", &i, &j)
#define scIll(i, j) scanf("%I64d %I64d", &i, &j)
#define sciii(i, j, k) scanf("%d %d %d", &i, &j, &k)
#define scddd(i, j, k) scanf("%lf %lf %lf", &i, &j, &k)
#define scIlll(i, j, k) scanf("%I64d %I64d %I64d", &i, &j, &k)
#define sciiii(i, j, k, l) scanf("%d %d %d %d", &i, &j, &k, &l)
#define scdddd(i, j, k, l) scanf("%lf %lf %lf %lf", &i, &j, &k, &l)
#define scIllll(i, j, k, l) scanf("%I64d %I64d %I64d %I64d", &i, &j, &k, &l)
 
#define lson l, m, rt<<1
#define rson m+1, r, rt<<1|1
#define lowbit(i) (i & (-i))
#define mem(i, j) memset(i, j, sizeof(i))
 
#define fir first
#define sec second
#define VI vector<int>
#define ins(i) insert(i)
#define pb(i) push_back(i)
#define pii pair<int, int>
#define VL vector<long long>
#define mk(i, j) make_pair(i, j)
#define all(i) i.begin(), i.end()
#define pll pair<long long, long long>
 
#define _TIME 0
#define _INPUT 0
#define _OUTPUT 0
clock_t START, END;
void __stTIME();
void __enTIME();
void __IOPUT();
using namespace std;
 
;
;
 
int n;
int ans1;
int xorSum[maxn];
int c[maxn];
int arr[maxn];
LL id[maxn];
LL PreSum[maxn];
LL ans2;
LL one[maxn][];
LL zero[maxn][];
 
inline void BitAdd(int i)
{
    ){
        c[i] ^= ;
        i += lowbit(i);
    }
}
 
int BitSum(int i)
{
    ) ;
    ;
    ){
        ret ^= c[i];
        i -= lowbit(i);
    }return ret;
}
 
int idx(LL key)
{
    , R = n;
    ;///过滤掉负数的情况、key<0 <=> ret+1 = 0
                 ///在树状数组里面不产生贡献
    while(L <= R){
        ;
        ;
        ;
    };
}
 
int main(void){__stTIME();__IOPUT();
 
    sci(n);
 
    ; i<=n; i++){
        sci(arr[i]);
        xorSum[i] = xorSum[i-] ^ arr[i];
        PreSum[i] = PreSum[i-] + arr[i];
    }
 
    ; i<; i++) zero[][i] = 1LL;
    ; i<=n; i++){
        ; j<; j++){
            one[i][j] = one[i-][j];
            zero[i][j] = zero[i-][j];
            if((xorSum[i] & (1LL<<j))){
                one[i][j]++;
                ans1 += zero[i-][j] * 1LL * (1LL<<j) % mod;
                if(ans1 >= mod) ans1 -= mod;
            }else{
                zero[i][j]++;
                ans1 += one[i-][j] * 1LL * (1LL<<j) % mod;
                if(ans1 >= mod) ans1 -= mod;
            }
        }
    }
 
    ; (1LL<<j)<=PreSum[n]; j++){
        ;
        ; i<=n; i++)
            id[i] = PreSum[i] & ((1LL << j + ) - );
 
        sort(id, id+n+);
 
        mem(c, );
        ; i<=n; i++){
            LL cur = PreSum[i] & ((1LL<< j + ) - );
            BitAdd(idx(cur));
            res ^= BitSum(idx(cur - (1LL<<j))) ^
                   BitSum(idx(cur + (1LL<<j))) ^
                   BitSum(idx(cur));
        }
        if(res) ans2 |= 1LL << j;
    }
 
    printf("%d %lld\n", ans1, ans2);
 
__enTIME();;}
 
void __stTIME()
{
    #if _TIME
        START = clock();
    #endif
}
 
void __enTIME()
{
    #if _TIME
        END = clock();
        cerr<<"execute time = "<<(double)(END-START)/CLOCKS_PER_SEC<<endl;
    #endif
}
 
void __IOPUT()
{
    #if _INPUT
        freopen("in.txt", "r", stdin);
    #endif
    #if _OUTPUT
        freopen("out.txt", "w", stdout);
    #endif
}