[笔记] 三元环 && 四元环计数

Thanks to i207M && iki9!

---

三元环计数

无向图的三元环计数

我们首先需要对无向边按一定规则定向：

设 \(in[u]\) 表示 \(u\) 的度数

• 若 \(in[u]>in[v]\) ，从 \(u\) 向 \(v\) 连边，反之则从 \(v\) 向 \(u\) 连边。
• 若 \(in[u]==in[v]\) ，我们从编号大的点向编号小的点连边。

此时这张图是一张有向无环图。

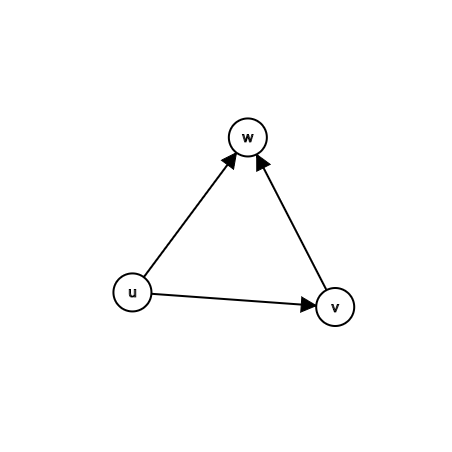
枚举每个点 \(u\) ，标记所有 \(u\) 的出点；然后枚举点 \(u\) 的出点 \(v\) ，再枚举 \(v\) 的出点 \(w\) ，若 \(w\) 被标记，则 \((u,v,w)\) 成三元环。

每个三元环只会在 \(u\) 被统计一次，如下图。

代码：

#define R register int
inline void main() {
	n=g(),m=g();
	for(R i=1,u,v;i<=m;++i) u=g(),v=g(),++d[u],++d[v],e[i]=edge(u,v);
	for(R i=1,u,v;i<=m;++i) { u=e[i].u,v=e[i].v;
		if(d[u]>d[v]||(d[u]==d[v]&&u>v) add(u,v);
		else add(v,u);
	} R ans=0;
	for(R u=1;u<=n;++u) { ++C;
		for(R i=fir[u];i;i=nxt[i]) flg[vr[i]]=C;
		for(R i=fir[u];i;i=nxt[i])
			for(R j=fir[vr[i]];j;j=nxt[j]) ans+=(flg[vr[j]]==C);
	} printf("%d\n",ans);
}

时间复杂度：

有向完全图（竞赛图）的三元环计数

\(C(n,3)-\sum_{u} C(in_u,2)\) ，\(in_u\) 表示 \(u\) 的入度。

---

四元环计数

还是要对边定向，同样类似上边的定向。

但此时注意枚举点 \(u\) 相邻的点 \(v\) 是原图中的边（而非重定向后的边），而枚举 \(v\) 相邻的点 \(w\) 则要是重定向后的点（可以交换图的顺序），原因是我们相当于是枚举两个部分拼起来。

还是在 \(u\) 被枚举一次，因为 \(rk[u]<rk[w]\).

代码：

inline bool cmp(const int& _this,const int& _that)
	{return d[_this]<d[_that]||(d[_this]==d[_that]&&_this<_that);}
#define con const int&
inline void main() {
	n=g(),m=g(); for(R i=1,u,v;i<=m;++i)
		u=g(),v=g(),e[u].push_back(v),e[v].push_back(u);
	for(R i=1;i<=n;++i) d[id[i]=i]=e[i].size();
	sort(id+1,id+n+1,cmp);
	for(R i=1;i<=n;++i) rk[id[i]]=i;
	for(R u=1;u<=n;++u) for(con v:e[u])
		if(rk[v]>rk[u]) f[u].push_back(v);
	for(R u=1;u<=n;++u) {
		for(con v:e[u]) for(con w:f[v]) if(rk[w]>rk[u]) ans+=c[w],++c[w]; //交换e与f的枚举顺序也是对的。
		for(con v:e[u]) for(con w:f[v]) if(rk[w]>rk[u]) c[w]=0; //清空桶。
	} printf("%lld\n",ans);
}

时间复杂度同上。

还有一种别的写法：

const int N=510;
int n,m; ll ans; bitset <N> e[N];
inline void main() {
	n=g(),m=g(); for(R i=1,u,v;i<=m;++i) u=g(),v=g(),e[u][v]=true,e[v][u]=true;
	for(R i=1,tmp;i<=n;++i) for(R j=i+1;j<=n;++j) {
		tmp=(e[i]&e[j]).count(); ans+=tmp*(tmp-1);
	} printf("%lld\n",ans>>2);
}

\(\mathcal{O}(n^3/32)\)

---

2019.10.28

18