DP,数论————洛谷P4317 花神的数论题(求1~n二进制中1的个数和)
玄学代码(是洛谷题解里的一位dalao小粉兔写的)
//数位DP(二进制)计算出f[i]为恰好有i个的方案数。
//答案为∏(i^f[i]),快速幂解决。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int mod=;
ll n,ans=;
ll c,f[];
ll qpow(ll b,ll e){
ll a=;
for(;e;b=b*b%mod,e>>=)
e&?a=a*b%mod:;
return a;
} int main(){
scanf("%lld",&n);
for(int j=;~j;--j){
for(int i=;i;--i)
f[i]+=f[i-];
if(n>>j&)++f[c++];
}++f[c];
for(int i=;i<=;++i)
ans=ans*qpow(i,f[i])%mod;
printf("%lld",ans);
return ;
}
下面是另一位dalaoStyx写的简单易懂的题解


代码如下
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mod 10000007
using namespace std; long long ans=,n,k,cnt,dp[][]; long long kasumi(long long a,long long b)
{
long long tmp=;
while(b)
{
if(b&) tmp=(tmp%mod)*a%mod;
a=(a%mod)*a%mod;
b>>=;
}
return tmp%mod;
} int main()
{
scanf("%lld",&n);
for(int i=; i<=; i++)
{
dp[i][]=;
}
for(int i=; i<=; i++)
{
dp[i][i]=;
}
for(int i=; i<=; i++)
{
for(int j=; j<i; j++)
{
dp[i][j]=dp[i-][j-]+dp[i-][j];
}
}
for(k=; k<=n; k<<=)
{
n-=k;
cnt++;
for(int j=; j<=cnt; j++)
{
ans=(ans%mod)*kasumi(j,dp[cnt][j])%mod;
ans%=mod;
}
}
cnt=;
for(int i=;i>=;i--)
{
if((1ll<<i)<=n)
{
for(int j=;j<=i+;j++)
{
ans=(ans%mod)*kasumi(j+cnt,dp[i+][j]);
ans%=mod;
}
cnt++;
n-=(1ll<<i);
}
}
printf("%lld\n",ans);
}
至于为什么不用扩展欧拉定理降幂,那是因为杨辉三角在总和等于1e15的时候 ,每一个数肯定不会爆longlong
DP,数论————洛谷P4317 花神的数论题(求1~n二进制中1的个数和)的更多相关文章
- 洛谷P4317 花神的数论题
洛谷题目链接 数位$dp$ 我们对$n$进行二进制拆分,于是就阔以像十进制一样数位$dp$了,基本就是套模板.. 接下来是美滋滋的代码时间~~~ #include<iostream> #i ...
- 洛谷 P4317 花神的数论题 || bzoj3209
https://www.lydsy.com/JudgeOnline/problem.php?id=3209 https://www.luogu.org/problemnew/show/P4317 设c ...
- 洛谷 P4317 花神的数论题(组合数)
题面 luogu 题解 组合数 枚举有多少个\(1\),求出有多少种数 扫描\(n\)的每一位\(1\), 强制选\(0\)然后组合数算一下有多少种方案 Code #include<bits/s ...
- P4317 花神的数论题
题目 洛谷 数学方法学不会%>_<% 做法 爆搜二进制下存在\(i\)位\(1\)的情况,然后快速幂乘起来 My complete code #include<bits/stdc++ ...
- P4317 花神的数论题 dp
这题我一开始就想到数位dp了,其实好像也不是很难,但是自己写不出来...常规套路,f[i][j][k][t],从后往前填数,i位,j代表是否卡着上沿,k是现在有几个1,t是想要有几个.记忆化搜索就ok ...
- 棋盘DP三连——洛谷 P1004 方格取数 &&洛谷 P1006 传纸条 &&Codevs 2853 方格游戏
P1004 方格取数 题目描述 设有N $\times N$N×N的方格图(N $\le 9$)(N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字00.如下图所示(见样例): A ...
- P4317 花神的数论题 动态规划?数位DP
思路:数位$DP$ 提交:5次(其实之前A过,但是调了调当初的程序.本次是2次AC的) 题解: 我们分别求出$sum(x)=i$,对于一个$i$,有几个$x$,然后我们就可以快速幂解决. 至于求个数用 ...
- Luogu P4317 花神的数论题
也是一道不错的数位DP,考虑先转成二进制后再做 转化一下问题,考虑统计出\([1,n]\)中在二进制下有\(i\)个\(1\)的方案数\(cnt_i\),那么答案显然就是\(\prod i^{cnt_ ...
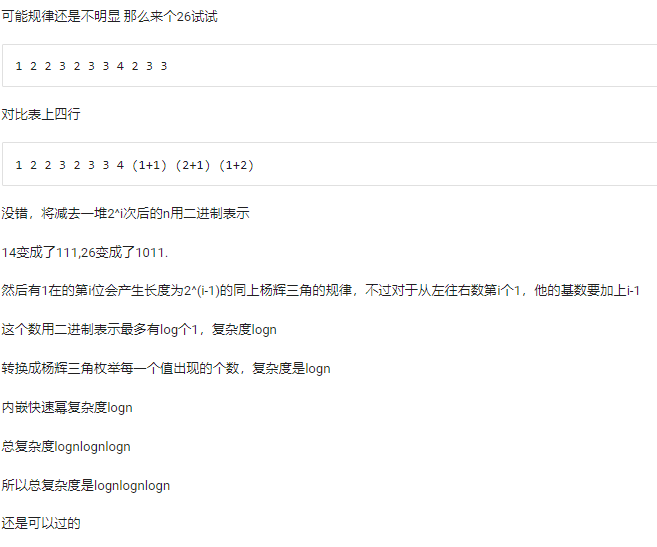
- P4317 花神的数论题,关于luogu题解粉兔做法的理解
link 题意 设 \(\text{sum}(i)\) 表示 \(i\) 的二进制表示中 \(1\) 的个数.给出一个正整数 \(N\) ,求 \(\prod_{i=1}^{N}\text{sum}( ...
随机推荐
- bzoj4009: [HNOI2015]接水果(整体二分)
题目描述 风见幽香非常喜欢玩一个叫做 osu!的游戏,其中她最喜欢玩的模式就是接水果.由于她已经DT FC 了The big black, 她觉得这个游戏太简单了,于是发明了一个更加难的版本. 首先有 ...
- 牛客练习赛3 F - 监视任务——贪心&&树状数组
题目 链接 $Reki$ 在课余会接受一些民间的鹰眼类委托,即远距离的狙击监视防卫..$Reki$ 一共接收到$m$份委托,这些委托与 $n$ 个直线排布的监视点相关.第 $i$ 份委托的内容为:对于 ...
- 正整数n拆分成几个不同的平方数——DFS&&打表
考虑将正整数n拆分成几个不同的平方数之和,比如30=1^2 + 2^2 + 5^2=1^2 + 2^2 + 3^2 + 4^2,而8不存在这样的拆分. #include<bits/stdc++. ...
- Python程序设计《集美大学各省成绩分析》
分析文件‘集美大学各省录取分数.xlsx’,完成以下功能: 1)集美大学2015-2018年间不同省份在本一批的平均分数,柱状图展示排名前10的省份, 2)分析福建省这3年各批次成绩情况,使用折线图展 ...
- vue上传大文件的解决方案
众所皆知,web上传大文件,一直是一个痛.上传文件大小限制,页面响应时间超时.这些都是web开发所必须直面的. 本文给出的解决方案是:前端实现数据流分片长传,后面接收完毕后合并文件的思路. 实现文件夹 ...
- gcc/g++以c++11编译
方法一: //在程序头加上预定义编译器命令 #pragma GCC diagnostic error "-std=c++11" //通过#pragma 指示 GCC编译器处理错误的 ...
- Java并发之同步工具类
1. CountDownlatch(计数器) 描述: 一个同步工具类,允许一个或多个线程等待其它线程完成操作 类图 通过指定的count值进行初始化,调用await方法的线程将被阻塞,直到count值 ...
- JavaWeb_(Spring框架)Spring整合Hibernate
Dao层类要继承HibernateDaoSupport.java父类 原先使用Hibernate框架hibernate.cfg.xml配置数据库 <hibernate-configuration ...
- 清空Linux缓存
清空Linux的缓存 sync > /proc/sys/vm/drop_caches > /proc/sys/vm/drop_caches > /proc/sys/vm/drop_c ...
- [转]五步git操作搞定Github中fork的项目与原作者同步
命令如下: git clone xxx-fork.git git remote add xxx xxx.git git fetch xxx git merge xxx/master git push ...
