JMeter 十一：参数化

Test Plan中定义变量

打开测试计划，在用户定义的变量中定义变量。

这里定义了一个HOST变量，值为“www.baidu.com”。

之后就可以使用 ${HOST} 来引用这个变量。

User Defined Variables中定义变量

线程组上右键 –> 添加 –> 配置元件 –> User Defined Variables 。

User Defined Variables最好放置在 Thread Group 的开头位置，或者 Test Plan下面。

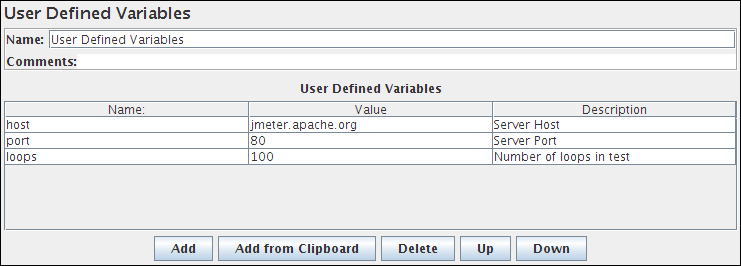
Name：输入变量名

Value：输入变量值

使用函数生成动态值

1. 打开函数助手对话框

JMeter –> 选项 –> 函数助手对话框

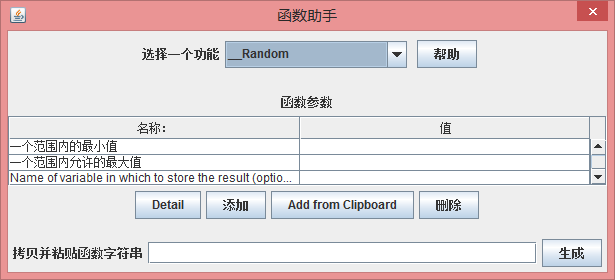
2. 生成字符串

选择一个功能：这里选择 “__Random”

选择一个功能之后，可以看到下方“函数参数”会随着变化。这里有3个函数参数。

一个范围内的最小值：生成的随机数最小范围，比如我们这里可以输入 “1”。

一个范围内允许的最大值：生成的随机数的最大范围，比如我们这里可以输入“100”。

Name of variable in which to store the result(option)：变量名称。比如这里可以输入”var1“。主要用作区分。可以不填。

上面都填写好之后，点击右下方的“生成”按钮，就可以生成函数字符串。这里就是“${__Random(1,100,var1)}”。

3. 使用

在需要用到随机数的地方，用“${__Random(1,100,var1)}”代替即可。

使用 Random Variable 控件生成变量

线程组上右键 –> 添加 –> 配置元件 –> Random Variable 。

Random Variable 会产生随机数字给变量。相当于 User Defined Variables + __Random(）函数的结合。

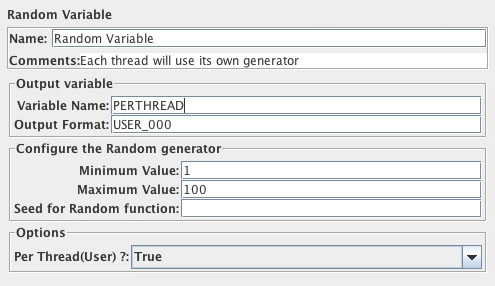
Variable Name: 储存随机数的变量名称。这里就是 “PERTHREAD”。

Output Format：输出格式。默认就是参数的数字。如果定义的话，比如这里是“USER_000”，假设产生的随机数是076，那么PERTHREAD=USER_076。

Minimum Value：产生随机数的最小值

Maximum Value：产生随机数的最大值

Random Seed：随机数产生器的种子。默认是当前时间。

Per Thread：如果选择False，则所有线程共享该随机数产生器。否则，每个线程拥有自己的随机数产生器。

从CSV文件读取数据

1. 新建配置元件

在线程组上右键 –> 添加 –> 配置元件 –> CSV Data Set Config 。

2. 配置元件配置

Filename：这里填写保存数据的文件名。可以是相对路径也可以是绝对路径。这里我把 log.csv和xx.jmx文件放在一个路径下，所以直接填写 log.csv即可。

File encoding：数据文件的编码。可以不填写。

Variable Names：这里填写保存数据的变量名。多个的话，以“，”进行分隔。比如这里填写“num1,num2”，到时候就可以使用 ${num1} 获取变量值。这里的顺序决定取到的数据的内容。

Delimiter：数据文件里面，变量的分隔符。默认是“，”。

Allow quoted data：这个不知道是啥意思。。。。。

Recycle on EOF ：数据读取到最后一行后，是否运行程序从第一行开始继续读取数据。

Stop thread on EOF: Recycle on EOF是 False的情况下，数据读取到最后一行，是否停止Thread。

Sharing mode ：这里可以选择哪些Thread 共享数据文件指针。比如选中“All threads”的话，当前Thread读取到第4行，下一个Thread就可以沿着第5行开始读。

3. 使用参数

在需要使用数据的地方，使用 ${num1}即可。

这里没有LoadRunner那么灵活，有多种取值方式。

我试验之后发现，数据是顺序取值。假设线程数是2，循环次数为10。那么第一个Thread 读取第一行数据，第二个Thread读取第二行数据，这样一直顺序下来。如果循环多次，也继续顺序下去，比如第一个Thread进行第二次循环时，就读取第3行数据。

4. 其他

这里也可以使用函数 __CSVRead 来读取CSV数据。这里不细说。