【找规律】【DFS】XVII Open Cup named after E.V. Pankratiev Stage 14, Grand Prix of Tatarstan, Sunday, April 2, 2017 Problem A. Arithmetic Derivative

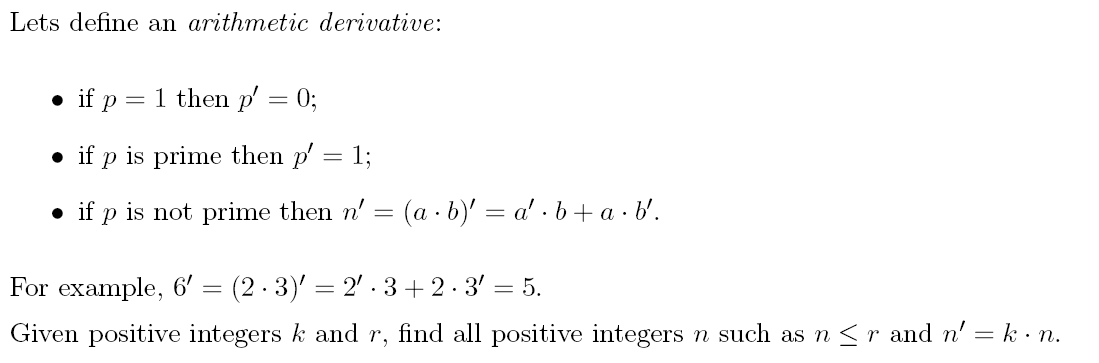
假设一个数有n个质因子a1,a2,..,an，那么n'=Σ(a1*a2*...*an)/ai。

打个表出来，发现一个数x，如果x'=Kx，那么x一定由K个“基础因子”组成。

这些基础因子是2^2,3^3,5^5,7^7,11^11,13^13。只有6个，K不超过30，于是可以dfs。

要注意搜索顺序（每次枚举的时候，都从大于等于前项的开始搜）和可行性剪枝（如果超过r则剪枝，虽说有可能爆long long，但其实整除就可以判，而且没有精度误差）。

#include<cstdio>
//#include<set>
#include<algorithm>
#include<cmath>
using namespace std;
//const long double EPS=0.0000000001;
typedef long long ll;
//set<ll>S;
ll base[11],path[1000010];
int pr[11];
int K,e;
ll r;
void dfs(int cur,int pre,ll now){
	if(cur==K){
//		if(S.find(now)==S.end()){
			path[++e]=now;
//			S.insert(now);
//		}
		return;
	}
	for(int i=pre;i<=6;++i){
		if(base[i]>r/now){
			break;
		}
		dfs(cur+1,i,now*base[i]);
	}
}
int main(){
//	freopen("a.in","r",stdin);
//	freopen("a1.out","w",stdout);
	pr[1]=2; pr[2]=3; pr[3]=5; pr[4]=7; pr[5]=11; pr[6]=13;
	for(int i=1;i<=6;++i){
		base[i]=1;
		for(int j=1;j<=pr[i];++j){
			base[i]*=(ll)pr[i];
		}
	}
	while(scanf("%d%lld",&K,&r)!=EOF){
		e=0;
//		S.clear();
		dfs(0,1,1ll);
		printf("%d\n",e);
		sort(path+1,path+e+1);
		if(e){
			for(int i=1;i<e;++i){
				printf("%lld ",path[i]);
			}
			printf("%lld\n",path[e]);
		}
	}
	return 0;
}