线性可分支持向量机与软间隔最大化--SVM(2)

线性可分支持向量机与软间隔最大化--SVM

---

给定线性可分的数据集

假设输入空间(特征向量)为，输出空间为。
输入
表示实例的特征向量，对应于输入空间的点；
输出
表示示例的类别。

我们说可以通过间隔最大化或者等价的求出相应的凸二次规划问题得到的分离超平面

以及决策函数：

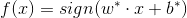
但是，上述的解决方法对于下面的数据却不是很友好， 例如，下图中黄色的点不满足间隔大于等于1的条件

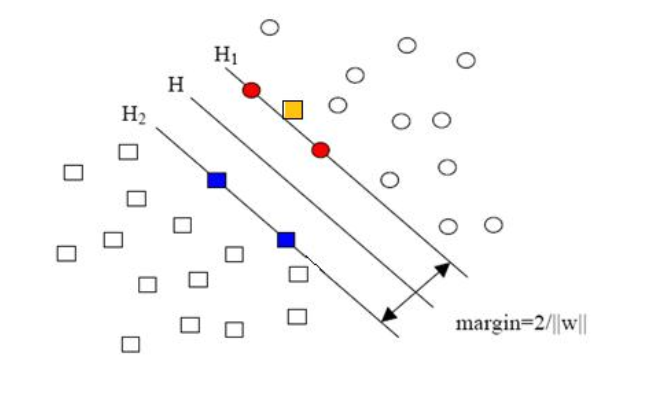
这样的数据集不是线性可分的， 但是去除少量的异常点之后，剩下的点都是线性可分的， 因此， 我们称这样的数据集是近似线性可分的。
对于近似线性可分的数据集，我们引入了松弛变量，使得函数间隔加上松弛变量大于等于1。这样就得到了下面的解决方案：

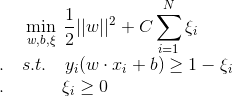
其中，每个样本点都对应一个松弛变量， C > 0 称为惩罚参数。C越大，对误分类的点的惩罚越大。
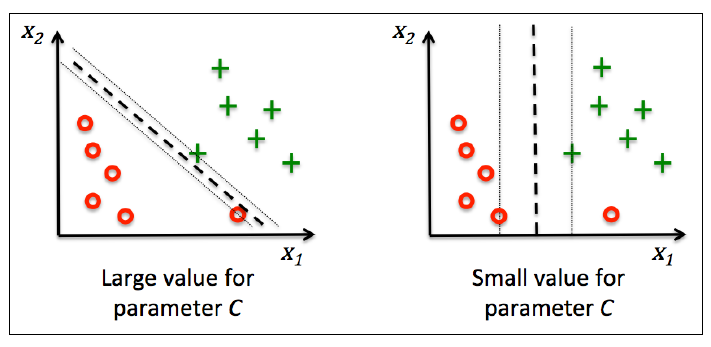
这个解决方案旨在使得间隔最大化的同时减少误分类个数。下图是C对分类的影响，左图是大C， 右图是小C：

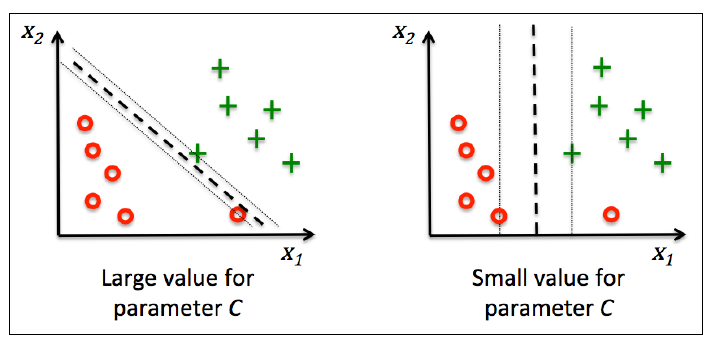
可以证明w是唯一的， 但是b不唯一，而是存在一个区间

---

下面来解决这个问题

首先引入拉格朗日函数（Lagrange Function）：

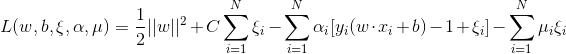
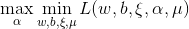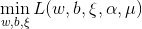他的对偶问题(参考拉格朗日对偶性(Lagrange duality))是极大极小问题， 首先求。对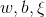求导，解法如下：

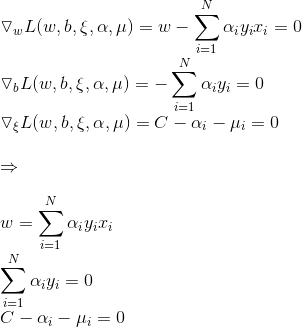
代入得到：

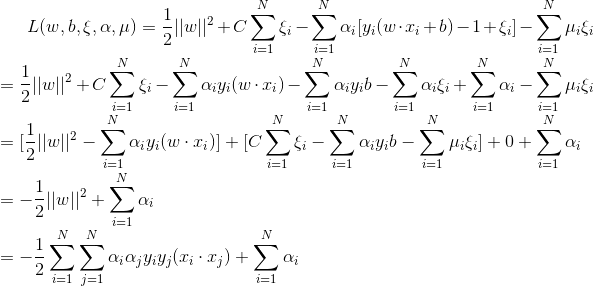
问题转化为：

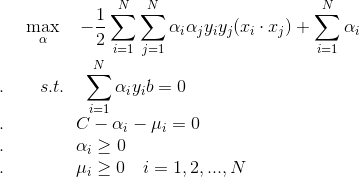
怎么求最优的w， b呢？
我们来看，原问题的KKT条件如下：

根据KKT条件的性质可以知道（参考拉格朗日乘子（Lagrange multify）和KKT条件)：

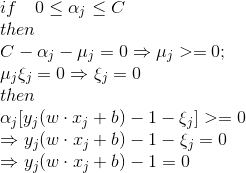
所以可以求得：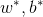

---

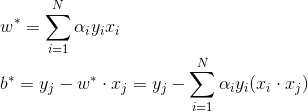
综上， 引入松弛变量后线性支持向量机算法为：

.

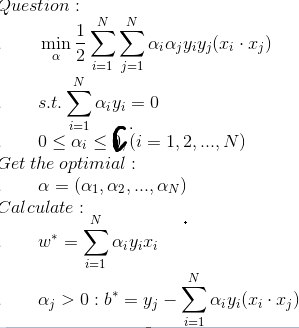
*我们引入的松弛变量去哪里了呢？为什么算法中没有了？
其实， 松弛变量在通过惩罚参数C隐式的作用。
我们可以改变C值，看看改变C哪些变量会随着改变。
增大C，由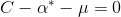知， 就更有可能大于0， 再根据，松弛变量取0就更简单， 这样就没有约束作用了。对整个数据集来说相当于是小的约束作用。
反之也可推出约束作用更强。
可以用这张图来解释：