洛谷p1006 传纸条 三维解法

原题目如下 原地址https://www.luogu.com.cn/problem/P1006

题目描述

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个 m 行 n 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 (1,1)，小轩坐在矩阵的右下角，坐标 (m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 0 表示），可以用一个 [0,100] 内的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

[0,100][0,100] 内的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

输入格式

第一行有两个用空格隔开的整数 m 和 n，表示班里有 m 行 n 列。

接下来的 m 行是一个 m×n 的矩阵，矩阵中第 i 行 j 列的整数表示坐在第 i 行 j 列的学生的好心程度。每行的 n 个整数之间用空格隔开。

m \times nm×n 的矩阵，矩阵中第 ii 行 jj 列的整数表示坐在第 ii 行 jj 列的学生的好心程度。每行的 nn 个整数之间用空格隔开。

输出格式

输出文件共一行一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

输入输出样例

  输入

3 3
0 3 9
2 8 5
5 7 0

输出

34

注：

1<=m,n<=50

以上为题目内容，已标明出处，如有侵权请联系我删除

思路：

可以看出纸条的传递有如下特点：

1.传过去传回来是两条路，但是事实上回来的路程仍然可以看作另一段“去程”，没有区别，所以为了简便看作在一个矩阵中找两条从左上角到右下角的路径

2.每人只帮一次，也就是两条路径不重合，且由于两条路的方向只有“右”和“下”，那么我们便可以想象出这两条路径它们的特点：一条在“左下”一条在“右上”，互不交叉。

所以显然我们不可以搜出好心值最大的一条路之后再搜出第二大的另一条，因为不交叉的性质会使得第二大的路无合法存在或者具有片面性。

然后根据数据范围 n， m <= 50，可以尝试动态规划的方式。

开始动态规划：

由于之前已提到不能把两条路分割开来看待，所以我们需要让这两条路“同时推进”。

那么需要找到表示每个状态的方法，考虑到每个点都是一对坐标“x， y”，所以走到某个点的最大好心值可以用F[x][y]表示

然后有两条路径，同时推进时，每一步都会走到两个点，所以每一步都可以用F[x1][y1][x2][y2]表示当两条路推进到（x1 ， y1）与（x2， y2）点时的最大好心值

显然，这样的话，在边界之内，每个状态F[x1][y1][x2][y2]由F[x1 - 1][y1][x2 - 1][y2], F[x1 - 1][y1][x2][y2 + 1], F[x1][y1 - 1][x2 - 1][y2], F[x1][y1 - 1][x2][y2 - 1]四个先前的状态转移而来，同时要考虑两路不交叉的特性，所以当上一个状态中的（x1 ， y1）与（x2， y2）重合时不要加入计算。最后显然，F[n - 1][m][n][m - 1]就是我们需要的答案。

复杂度分析

这样最大所需的存储空间是int * 50的四次幂 也就是6250000 * 4字节 == 25000000B == 25M，符合范围要求

时间复杂度是O（m * m * n * n）是6250000接近1e7，此方法是可以通过此题的，但是如果常数处理不当可能会有问题。而且如果题中的n ，m范围若扩大到200的话，此方法便行不通了。

核心优化

显然降维是首要任务，首先我们可以发现，四维解法中，由于两条路同时推进，有一些状态是根本不可能存在的，除了（x1 ， y1）与（x2， y2）重合的状态，还有比如F[1][3][4][1]，显然（1 ， 3）与（4， 1）分别需要一步与两步才能走得到，根本不可能来表示一个状态。另外，可以发现，由于不交叉，所以下面一条路的下方的点都不可能是上面的那条路的经过的点。

这样便发现了大量的不存在的状态

我们从条路同时推进时，到达的两点之间的关系来考虑：

首先上面的那条路的起点必然在（2， 1），下面的起点则在（1， 2），这两点在同一条左下到右上的斜线上

而过程中，方向只有“右”和“下”，显然我们可以发现，对一条路来说，它的下一步，总是会走到同一条斜线上（如图）

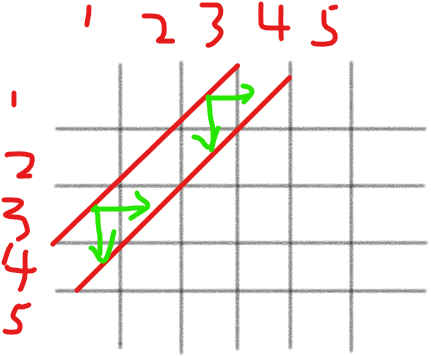
那么显然，两条路的下一步肯定也会处于同一条左下到右上的斜线上。

而我们知道，在本题坐标系中，这样的一条斜线上，x + y 等于一个常数，且对于不同的在此方向的斜线来说，这个常数是不同的

那么也就是说，

　　x1 + y1 == x2 +  y2

关系找到了。

这样我们就可以开始降维了，因为每一步两点会处于同一条左下到右上的斜线上，所以可以用一个维度来表示现在推进到了哪一条斜线上，令C = x + y

同时，我们知道，与这条斜线垂直方向的斜线上，x - y的值也是一个类似的常数，所以对于目前推进到的这条直线，我们可以在上面用x - y的值来代表一条路在此“左下-右上”方向斜线上的位置

所以，另外两个维度用此点所在的“左上-右下”方向的斜线的”x - y”值表示就可以了，同时为了防止出现负数，我们让y - x 加 n，令D = n + x - y

同时为了简便，在读入好心值时，我们就把这些值从x - y坐标转化为“C - D“坐标

所以显然：

F[C][D1][D2] = max(F[C - 1][D1 + 1][D2  - 1], F[C - 1][D1 - 1][D2 - 1], F[C - 1][D1 + 1][D2 + 1], F[C - 1][D1 + 1][D2 + 1]) + W[C][D1] + W[C][D2]; 同时要注意D1 < D2 恒成立，同时忽略上一步两点重合的情况就可以了

同时，在同一条“左下-右上”斜线上时，我们循环中的D值应该是递加、递减2的

显然，F[m + n - 1][n + 1][n - 1]即为我们要求的结果

最后

相信看到这个数组以及图片之后我们就可以想到了，C这一维数组空间，完全是可以去掉的，因为相邻的两层状态所占空间不冲突，而后面的状态只需要上一层的状态来转移，正好覆盖掉上上层状态完成更替，所以，用F[D1][D2]就可以了，所以最终结果是F[n + 1][n - 1]

复杂度分析

这样，每一维最大为100，所需空间是int * 100 * 100 = 10000B * 4 = 40KB，空间大大减少

时间复杂度最大时小于O（100 / 2 * 100 / 2 * （m + n）） 即小于250000，远小于限制

AC代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;

int abss(int a)
{
    return a <  ? -a : a;
}
int n, m;
int aa[][] = {  };
int bb[][] = {  };
int ff[][];
int main()
{
    cin >> m >> n;
    for (int i = ; i <= m; ++i)
    {
        for (int j = ; j <= n; ++j)
        {
            cin >> aa[i][j];
            bb[i + j][m + (j - i)] = aa[i][j];//加m防止出现负数下标
        }
    }
    ff[m - ][m + ] = bb[][m - ] + bb[][m + ];
    for (int i = ; i < n + m; ++i)
    {
        for (int j = abss(i -  - m); j < m + n -  - abss(n - i + ); j += )
        {
            for (int k = m + n -  - abss(n - i + ); k > j; k -= )
            {
                ff[j][k] = ff[j - ][k + ] + bb[i][j] + bb[i][k];
                if (j +  < k - )
                {
                    ff[j][k] = max(ff[j][k], ff[j + ][k - ] + bb[i][j] + bb[i][k]);
                }
                if (j +  < m + n -  - abss(n - i + ))
                {
                    ff[j][k] = max(ff[j][k], ff[j + ][k + ] + bb[i][j] + bb[i][k]);
                }
                ff[j][k] = max(ff[j][k], ff[j - ][k - ] + bb[i][j] + bb[i][k]);
            }
        }
    }
    printf("%d\n", ff[n - ][n + ]);
    return ;
}

本题从四维时间/四维空间 降为三维时间/二维空间的关键，是找到不存在的无用状态，并利用方向限制带来的坐标之间的关系，最终将x-y坐标进行转换，从斜线的角度去思考矩阵

30\%30% 的数据，1 \le m,n \le 101≤m,n≤10； 对于 100\%100% 的数据满足：1 \le m,n \le 501≤m,n≤5030\%30% 的数据，1 \le m,n \le 101≤m,n≤10； 对于 100\%100% 的数据满足：1 \le m,n \le 501≤m,n≤50