机器学习实战：意大利Covid-19病毒感染数学模型及预测

作者：Gianluca Malato

deephub翻译组：刘欣然

当今世界正在与一个新的敌人作斗争，那就是Covid-19病毒。

该病毒自首次在中国出现以来，在世界范围内迅速传播。不幸的是，意大利的Covid-19感染人数是欧洲最高的，为19人。我们是西方世界第一个面对这个新敌人的国家，我们每天都在与这种病毒带来的经济和社会影响作斗争。

在本文中，我将用Python向您展示感染增长的简单数学分析和两个模型，以更好地理解感染的演变。

数据收集(Data collection)

意大利民防部门每天都会更新感染者的累积数据。这些数据在GitHub上作为开放数据公开在Github这里：

https://raw.githubusercontent.com/pcm-dpc/COVID-19/master/dati-andamento-nazionale/dpc-covid19-ita-andamento-nazionale.csv
我的目标是创建迄今为止受感染人数（即实际感染人数加上已感染人数）的时间序列模型。这些模型具有参数，这些参数将通过曲线拟合进行估算。

我们用Python来做。

首先，让我们导入一些库。

importpandas as pd
importnumpy as np
from datetime import datetime,timedelta
from sklearn.metrics import mean_squared_error
from scipy.optimize import curve_fit
from scipy.optimize import fsolve
import matplotlib.pyplot as plt
%matplotlib inline

现在，让我们看一下原始数据。

url = https://raw.githubusercontent.com/pcm-dpc/COVID-19/master/dati-andamento-nazionale/dpc-covid19-ita-andamento-nazionale.csv
df =pd.read_csv(url)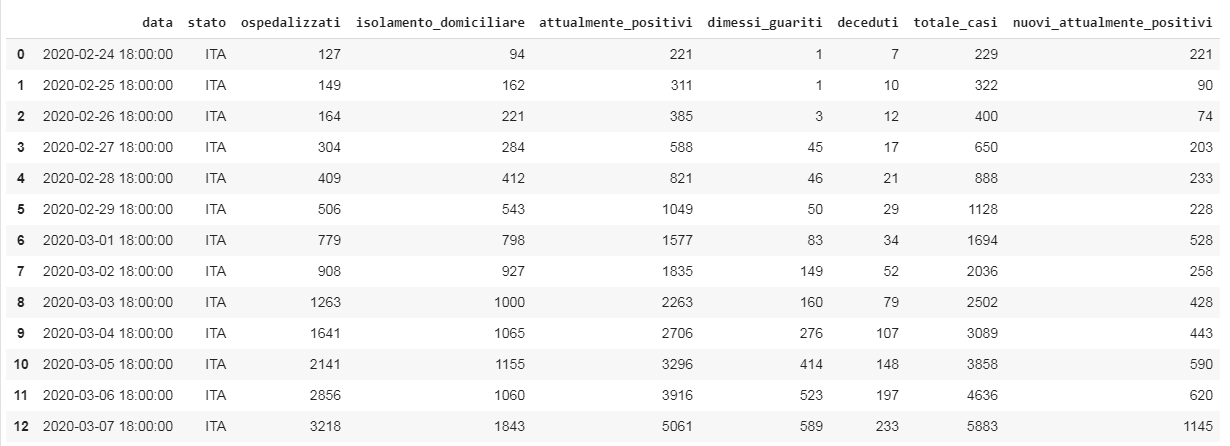

我们需要的列是' totale_casi '，它包含到目前为止的累计感染人数。

这是原始数据。现在，让我们为分析做准备。

数据准备（Data preparation）

首先，我们需要将日期改为数字。我们将从一月一日起开始算。

df =df.loc[:,['data','totale_casi']]
FMT ='%Y-%m-%d %H:%M:%S'
date =df['data']
df['data']= date.map(lambda x : (datetime.strptime(x, FMT) -datetime.strptime("2020-01-01 00:00:00", FMT)).days  )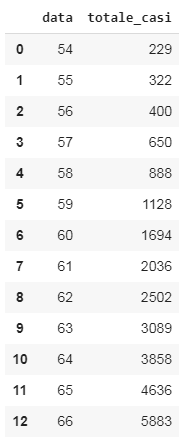

现在，我们可以分析要参加测试的两个模型，分别是逻辑函数（logistic function）和指数函数（exponential function）。

每个模型都有三个参数，这些参数将通过对历史数据进行曲线拟合计算来估计。

logistic模型（The logistic model）

logistic模型被广泛用于描述人口的增长。感染可以被描述为病原体数量的增长，因此使用logistic模型似乎是合理的。

这个公式在数据科学家中非常有名，因为它被用于逻辑回归分类器，并且是神经网络的一个激活函数。

logistic函数最一般的表达式为:

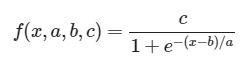
在这个公式中，我们有变量x（它是时间）和三个参数:a,b,c。

•a为感染速度
•b为感染发生最多的一天
•c是在感染结束时记录的感染者总数

在高时间值时，被感染的人数越来越接近c值，也就是我们说感染已经结束的时间点。这个函数在b点也有一个拐点，也就是一阶导数开始下降的点(即感染开始减弱并下降的峰值)。

让我们在Python中定义模型：

def logistic_model(x,a,b,c):
    return c/(1+np.exp(-(x-b)/a))

我们可以使用scipy库中的curve_fit函数从原始数据开始估计参数值和错误。

x =list(df.iloc[:,0])
y =list(df.iloc[:,1])fit = curve_fit(logistic_model,x,y,p0=[2,100,20000])

这里是一些值：

·       a: 3.54
·       b: 68.00
·       c: 15968.38

该函数也返回协方差矩阵，其对角值是参数的方差。取它们的平方根，我们就能计算出标准误差。

errors= [np.sqrt(fit[1][i][i]) for i in [0,1,2]]

·       a的标准误差：0.24
·       b的标准误差：1.53
·       c的标准误差：4174.69

这些数字给了我们许多有用的见解。

预计感染人数在感染结束时为15968+/-4174。

感染高峰预计在2020年3月9日左右。

预期的感染结束日期可以计算为受感染者累计计数四舍五入约等于到最接近整数的c参数的那一天。

我们可以使用scipy的fsolve函数来计算出定义感染结束日的方程的根。

sol =int(fsolve(lambda x : logistic_model(x,a,b,c) - int(c),b))

求解出来时间是2020年4月15日。

指数模型（Exponential model）

logistic模型描述了未来将会停止的感染增长，而指数模型描述了不可阻挡的感染增长。例如，如果一个病人每天感染2个病人，1天后我们会有2个感染，2天后4个，3天后8个，等等。

最通用的指数函数是：

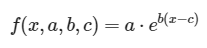
变量x是时间，我们仍然有参数a, b, c，但是它的意义不同于logistic函数参数。

让我们在Python中定义这个函数，并执行与logistic增长相同的曲线拟合过程。

def exponential_model(x,a,b,c):

    return a*np.exp(b*(x-c))exp_fit =curve_fit(exponential_model,x,y,p0=[1,1,1])

参数及其标准差为:

·       a: 0.0019 +/- 64.6796
·       b: 0.2278 +/- 0.0073
·       c: 0.50 +/- 144254.77

画图

我们现在有了所有必要的数据来可视化我们的结果。

pred_x= list(range(max(x),sol))
plt.rcParams['figure.figsize']= [7, 7]
plt.rc('font',size=14)

## Realdata
plt.scatter(x,y,label="Real data",color="red")
#Predicted logistic curve
plt.plot(x+pred_x,[logistic_model(i,fit[0][0],fit[0][1],fit[0][2]) for i inx+pred_x], label="Logistic model" )
#Predicted exponential curve
plt.plot(x+pred_x,[exponential_model(i,exp_fit[0][0],exp_fit[0][1],exp_fit[0][2])for i in x+pred_x], label="Exponential model" )
plt.legend()
plt.xlabel("Days since 1 January 2020")
plt.ylabel("Total number of infected people")
plt.ylim((min(y)*0.9,c*1.1))plt.show()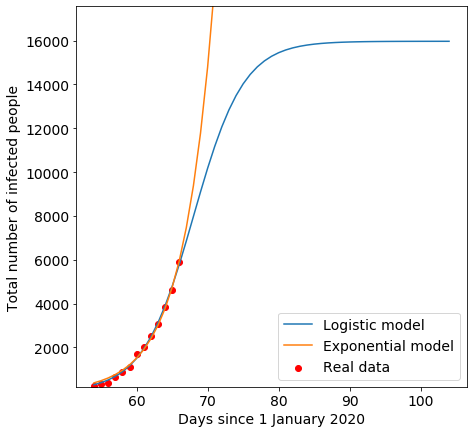

这两条理论曲线似乎都很接近实验趋势。哪一个更好?让我们看一下残差(residuals.)。

残差分析

残差是指各实验点与相应理论点的差值。我们可以通过分析两种模型的残差来验证最佳拟合曲线。在第一次近似中，理论和实验数据的均方误差越小，拟合越好。

y_pred_logistic=[logistic_model(i,fit[0][0],fit[0][1],fit[0][2])
for iin x]y_pred_exp = [exponential_model(i,exp_fit[0][0], exp_fit[0][1], exp_fit[0][2]) for iin  x]
mean_squared_error(y,y_pred_logistic)
mean_squared_error(y,y_pred_exp)

Logistic模型MSE(均方误差):8254.07

指数模型MSE: 16219.82

哪个是正确的模型？

残差分析似乎指向逻辑模型。很可能是因为感染应该会在将来的某一天结束；即使每个人都会被感染，他们也会适当地发展出免疫防御措施以避免再次感染。只要病毒没有发生太多变异(例如，流感病毒)，这就是正确的模型。

但是有些事情仍然让我担心。自感染开始以来，我每天都在拟合logistic曲线，而且每天都有不同的参数值。感染的人数最终会增加，最大感染日通常是当天或第二天（与该参数的1天标准误差是一致的）。

这就是为什么我认为，尽管逻辑模型似乎是最合理的模型，但是曲线的形状可能会由于新的感染热点，政府约束感染的行动措施等外在影响而发生变化。

因此，我认为这个模型的预测只有在感染高峰期之后的几周内才会开始有用。

原文地址：https://imba.deephub.ai/p/cced87c064f711ea90cd05de3860c663