Floyd —Warshall（最短路及其他用法详解）

一、多元最短路求法

多元都求出来了，单源的肯定也能求。

思想是动态规划的思想：从任意节点A到任意节点B的最短路径不外乎2种可能，1是直接从A到B，2是从A经过若干个节点X到B。所以，我们假设Dis(AB)为节点A到节点B的最短路径的距离，对于每一个节点X，我们易写出状态转移方程Dis(AB) =min（Dis(AX) + Dis(XB) ，Dis(AB)）这样一来，当我们遍历完所有节点X，Dis(AB)中记录的便是A到B的最短路径的距离。

memset（Dis，0x3f,sizeof(Dis);
//初始化，这里采用0x3f而非0x7f，是当两个0x7f7f7f7f相加符号变号成为一个无穷小量。
void floyd(int N）
{
	int i,j,k;
	for(k=0;k<N;k++)
	{
		for(i=0;i<N;i++)
		{
			for(j=0;j<N;j++)
			{
				if(Dis[i][k]+Dis[k][j]<Dis[i][j])
				{
					Dis[i][j]=Dis[i][k]+Dis[k][j];

				}
			}
		}
	}
}

这里一定要把K写到外边，需要先更新K前面的点在更新K后的点才有意义。

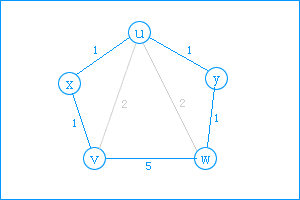
结合代码 并参照上图所示 我们来模拟执行下 这样才能加深理解：

第一关键步骤：当k执行到x，i=v,j=u时，计算出v到u的最短路径要通过x，此时v、u联通了。

第二关键步骤：当k执行到u，i=v，j=y，此时计算出v到y的最短路径的最短路径为v到u，再到y(此时v到u的最短路径上一步我们已经计算过来，直接利用上步结果)。

第三关键步骤：当k执行到y时，i=v，j=w，此时计算出最短路径为v到y(此时v到y的最短路径长在第二步我们已经计算出来了)，再从y到w。

依次扫描每一点(k)，并以该点作为中介点，计算出通过k点的其他任意两点(i,j)的最短距离，这就是floyd算法的精髓！同时也解释了为什么k点这个中介点要放在最外层循环的原因.

完整代码：

#include<iostream>
#include<stack>
using namespace std;
#define MAX 1000
int Graph[MAX][MAX];
int Dis[MAX][MAX];
#define infinite 1000
int path[MAX][MAX];

void floyd(int N)
{
	int i,j,k;
	for(k=0;k<N;k++)
	{
		for(i=0;i<N;i++)
		{
			for(j=0;j<N;j++)
			{
				if(Dis[i][k]+Dis[k][j]<Dis[i][j])
				{
					Dis[i][j]=Dis[i][k]+Dis[k][j];
					path[i][j]=k;

				}
			}
		}
	}

}

void print_path(int N)
{
	int i,j;
	for(i=0;i<N;i++)
	{
		for(j=0;j<N;j++)
		{
			if((i!=j) &&Dis[i][j]!=infinite)
			{
				cout<<i+1<<"----"<<j+1<<"   distance:"<<Dis[i][j]<<endl;
				cout<<"path:"<<endl;
				int k=j;
				stack <int> ph;
				do
				{
					k=path[i][k];
					ph.push(k);
				}while(k!=i);
				cout<<ph.top()+1;
				ph.pop();
				while(!ph.empty())
				{
					cout<<"->"<<ph.top()+1;
					ph.pop();
				}
				cout<<"->"<<j+1<<endl;
			}
		}
	}
}

void main()
{
	int N,i,j;
	cin>>N;
	for(i=0;i<N;i++)
	{
		for(j=0;j<N;j++)
		{
			int g;
			cin>>g;
			Graph[i][j]=g;
			Dis[i][j]=g;
		}
	}
//初始化路径
		for(i=0;i<N;i++)
		{
			for(j=0;j<N;j++)
			{
				path[i][j]=i;
			}
		}
	floyd(N);
	print_path(N);
    system("pause");
}

二、连通性

讲Dis[i][j]不连联通时设置为0，联通时设置为1.

则可得状态转移方程

dis[i][j]=dp[i][j]||(dp[i][k]&&dp[k][j]);

跟上面代码除了状态转移方程之外还有初始化不同，这个都初始化为0；

其余都一样。要么ij直接连通，要么ij通过K联通。

void floyd(int N)
{
	int i,j,k;
	for(k=0;k<N;k++)
	{
		for(i=0;i<N;i++)
		{
			for(j=0;j<N;j++)
			{
				if((dp[i][k]&&dp[k][j])&&!Dis[i][j])
				{
					Dis[i][j]=Dis[i][k]+Dis[k][j];
					path[i][j]=k;
				}
			}
		}
	}
}

三、求无向图中可以删除一些边，使得任意两点的最短路不改变，求这些边能删除的最大的条数。（最小生成树问题）

首先先在输入边的时候将重边去掉，保留最小的。

然后进行佛洛依德。

如果原来两点的最短距离大于经过第三个点的最短距离的话，那么我们就将这两点的最短距离

替换成经过第三条边的最短距离，当循环节结束后通过对比两点之间的距离变化，即可知哪些边将被删去。但是~~~当两点之间本来没有边的情况下，我们肯定是经过第三个点所到达的。那么就没有替换原来的边，这种情况的话，就直接continue；

四、无向图最小环

若用dis[i][j]表示ij之间的最小值，则由i j 加线外一点k的环值为dis[i][j]+length[i][k]+length[k][j];

枚举中间点k，在用其更新最短路前，先找最小环，令1<=i<j<k，即k点必定不在i,j的最短路上，则这个环中至少有三个点，可得状态转移方程 ans=min(ans,dis[i][j]+length[i][k]+length[k][j]);

#include <cstdio>
#include <cstring>
#include <map>
#include <queue>
#include <algorithm>

using namespace std;

struct Node {
    int s[9];//s数组表示包括本端所连的fence

    Node() {
        memset(s,0,sizeof(s));
    }

    bool operator < (const Node& a) const {
    for(int i=0;i<9;++i)
        if(s[i]<a.s[i])
            return true;
        else if(s[i]>a.s[i])
            return false;
    return false;
}

bool operator ==(const Node& a) const {
    for(int i=0;i<9;++i)
        if(s[i]!=a.s[i])
            return false;
    return true;
}

}fence[205];
int n,s,ls,ns,n1s,n2s,sta,des,cur;
int g[105][105],cnt=0,dis[105][105];
bool vis[105];
map<Node,int> mp;
int floyd() {
    int ans=0x1f1f1f1f;
    for(int i=1;i<=n;++i)
        for(int j=i;j<=n;++j)
            dis[i][j]=dis[j][i]=g[i][j];

    for(int k=1;k<=cnt;++k) {
        for(int i=1;i<k;++i)//寻找最小环
        for(int j=i+1;j<k;++j)
            if(dis[i][j]+g[i][k]+g[k][j]<ans)//由于此处会存在三个INF相加，所以INF设为0x1f1f1f1f
                ans=dis[i][j]+g[i][k]+g[k][j];
    for(int i=1;i<=n;++i)//更新最短路
        for(int j=1;j<=n;++j)
            if(dis[i][j]>dis[i][k]+dis[k][j])
                dis[i][j]=dis[i][k]+dis[k][j];
}
return ans;
}
int main() {
    //freopen("fence6.in","r",stdin);
   // freopen("fence6.out","w",stdout);

    memset(g,0x1f,sizeof(g));
    scanf("%d",&n);
    for(int i=1;i<=n;++i) {//读入边数据，并给每个点标一个数
        scanf("%d%d%d%d",&s,&ls,&n1s,&n2s);
        fence[i<<1].s[8]=fence[(i<<1)|1].s[8]=s;

    while(n1s-->0)
        scanf("%d",&fence[i<<1].s[n1s]);
    sort(fence[i<<1].s,fence[i<<1].s+9);
    if(mp[fence[i<<1]]==0)
        mp[fence[i<<1]]=++cnt;

    while(n2s-->0)
        scanf("%d",&fence[(i<<1)|1].s[n2s]);
    sort(fence[(i<<1)|1].s,fence[(i<<1)|1].s+9);
    if(mp[fence[(i<<1)|1]]==0)
        mp[fence[(i<<1)|1]]=++cnt;

    sta=mp[fence[i<<1]];
    des=mp[fence[(i<<1)|1]];
    g[sta][des]=g[des][sta]=ls;//边信息转成点信息
}
printf("%d\n",floyd());
return 0;
}

五、传递闭包问题

邻接矩阵是显示两点的直接关系，如a直接能到b，就为1。而传递闭包显示的是传递关系，如a不能直接到c，却可以通过a到b到d再到c，因此a到c为1。



另外矩阵A进行自乘即A^{{2}得到的矩阵中，为1的值表示走最多两步可以到达。A}{3}矩阵中为1的值表示，最多走三步可以到达。

简单来说，就是有向图确定先后顺序。

/*
题目：n头牛进行m场比赛，问能确定排名的有多少头牛。
  解答：构造一个n个点的有向图，如果牛a胜b，那么a->b，如果a->b，b->c，则有a->c，这个用floyd。
  最后得到该图的传递闭包link的二维数组。最后统计每一个点入度和出度和为n-1的点的个数即可。
*/
#include<stdio.h>
#include<string.h>
const int MAX=105;
/*
有向图的传递闭包！
注意传递之前一定要初始化！
如果i!=j&&(i,j)不属于E(边的集合) t[i][j]=0;
如果i=j||(i,j)属于E(边的集合)     t[i][j]=1;
*/

//传递闭包
void Transitive_Closure(int n,bool t[][MAX])
{
	int i,j,k;
	for(k=1;k<=n;k++)
		for(i=1;i<=n;i++)
			for(j=1;j<=n;j++)
				t[i][j]=t[i][j]|(t[i][k]&t[k][j]);
}
int main()
{
	int n,i,j,m,st,ed,sum,num;
	bool t[MAX][MAX];
	while(scanf("%d%d",&n,&m))
	{
		if(n==0&&m==0)
			return 0;
		memset(t,false,sizeof(t));
		for(i=1;i<=n;i++)
			t[i][i]=true;
		for(i=1;i<=m;i++)
		{
			scanf("%d%d",&st,&ed);
			t[st][ed]=true;
		}//上面的代码都是初始化
		Transitive_Closure(n,t);
		sum=0;
		for(i=1;i<=n;i++)
		{
			num=0;
			for(j=1;j<=n;j++)
				if(i==j)
					continue;
				else
					num+=(t[i][j]||t[j][i]);//统计出度和入度的个数!
				sum+=(num==n-1);
		}
		printf("%d\n",sum);
	}
	return 0;
}
/*
5 5
4 3
4 2
3 2
1 2
2 5
  2
*/