变分推断到变分自编码器(VAE)

EM算法

EM算法是含隐变量图模型的常用参数估计方法，通过迭代的方法来最大化边际似然。

带隐变量的贝叶斯网络

给定N 个训练样本D={x⁽ⁿ⁾}，其对数似然函数为：

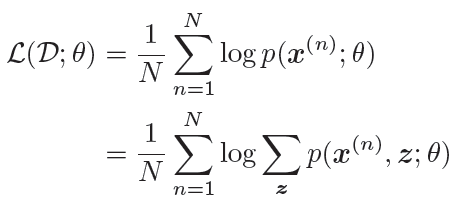
通过最大化整个训练集的对数边际似然L(D; θ)，可以估计出最优的参数θ^∗。然而计算边际似然函数时涉及p(x) 的推断问题，需要在对数函数的内部进行求和（或积分）

注意到，对数边际似然log p(x; θ) 可以分解为

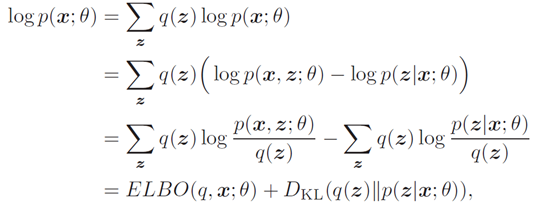
其中D_KL(q(z)∥p(z|x; θ))为分布q(z)和后验分布p(z|x; θ)的KL散度.

由于D_KL(q(z)∥p(z|x; θ)) ≥ 0，并当且仅当q(z) = p(z|x; θ) 为0，因此 ELBO(q, x; θ) 为log p(x; θ) 的一个下界

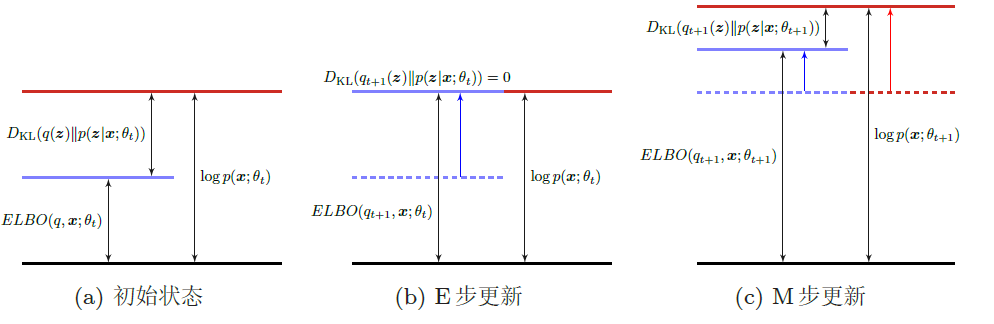
EM算法具体分为两个步骤：E步和M步。这两步不断重复，直到收敛到某个局部最优解。在第t 步更新时，E步和M步分别为

• E步（Expectation Step）：固定参数θ_t，找到一个分布使得ELBO(q, x; θ_t)最大，即等于log p(x; θ_t)

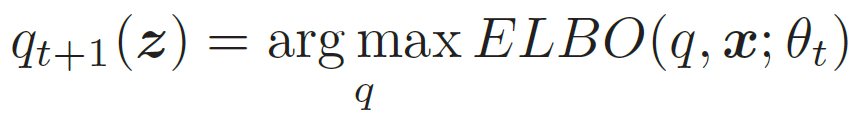
• • 所以我们希望q(z) = p(z|x, θ_t) ，这样ELBO(q, x; θ_t)最大。而计算后验分布p(z|x; θ)是一个推断（Inference）问题。如果z是有限的一维离散变量 。（比如混合高斯模型），计算起来还比较容易。否则，p(z|x; θ) 一般情况下很难计算，需要通过变分推断的方法来进行近似估计
• M步（Maximization Step）：固定q_t+1(z)，找到一组参数使得证据下界最大，即

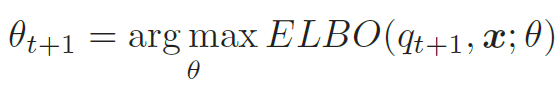
EM算法在第t 步迭代时的示例

变分自编码

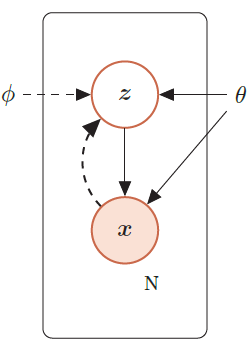
变分自编码器

生成模型的联合概率密度函数

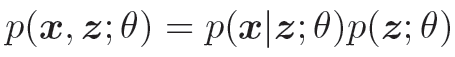
给定一个样本x，其对数边际似然log p(x; θ) 可以分解为

其中q(z; ϕ)是额外引入的变分密度函数, 其参数为ϕ，ELBO(q, x; θ, ϕ)为证据下界，

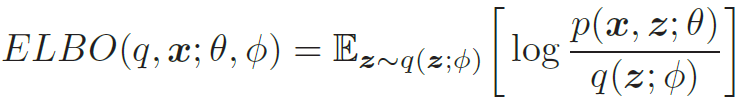
最大化对数边际似然log p(x; θ) 可以用EM算法来求解，具体可以分为两步：

　　E步：寻找一个密度函数q(z; ϕ) 使其等于或接近于后验密度函数p(z|x; θ)；
　　M步：保持q(z; ϕ) 固定，寻找θ 来最大化ELBO(q, x; θ, ϕ)。

PS: 当p(z|x; θ)比较复杂时，很难用简单的变分分布q(z; ϕ)去近似，此时，q(z; ϕ)也相对比较复杂，除此之外，概率密度函数p(x|z; θ)一般也比较复杂。那怎么办呢？很简单，我们可以用神经网络来近似这两个复杂的概率必读函数。这就是变分自编码器（Variational AutoEncoder，VAE）的精髓。

• 推断网络：用神经网络来估计变分分布q(z; ϕ)，理论上q(z; ϕ) 可以不依赖x。但由于q(z; ϕ) 的目标是近似后验分布p(z|x; θ)，其和x相关，因此变分密度函数一般写为q(z|x; ϕ)。推断网络的输入为x，输出为变分分布q(z|x; ϕ)。
• 生成网络：用神经来估计概率分布p(x|z; θ)，生成网络的输入为z，输出为概率分布p(x|z; θ)。

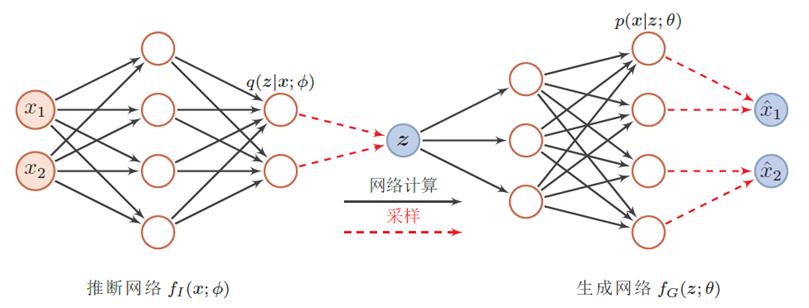
变分自编码器的网络结构

推断网络

为了简单起见，假设q(z|x; ϕ) 是服从对角化协方差的高斯分布

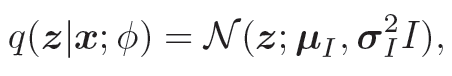
均值和方程我们可以用推断网络f_I(x; ϕ)来预测

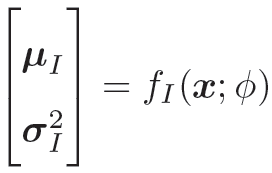
目标：q(z|x; ϕ) 尽可能接近真实的后验p(z|x; θ)，

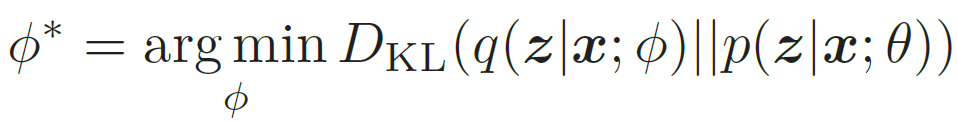
然而，直接计算上面的KL散度是不可能的，因为p(z|x; θ) 一般无法计算。注意到，

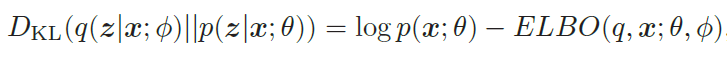
所以，推断网络的目标函数为

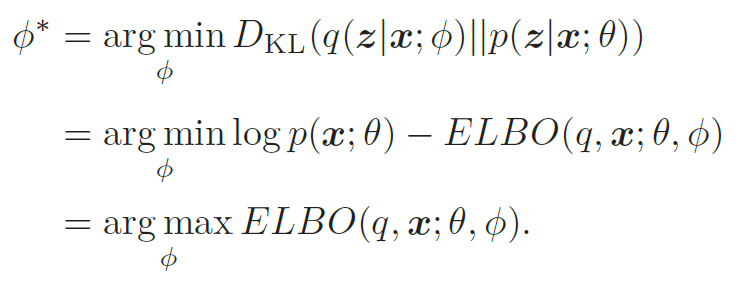
生成网络

生成模型的联合分布p(x, z; θ) 可以分解为两部分：隐变量z 的先验分布p(z; θ) 和条件概率分布p(x|z; θ)，

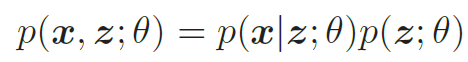
为了简单起见，我们假设先验分布

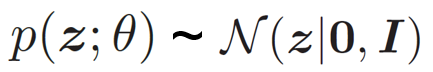
而条件概率分布p(x|z; θ)我们可以用生成网络来建模，里面的参数可以用生成网络计算得到。

根据变量x 的类型不同，可以假设p(x|z; θ) 服从不同的分布族

• x in {0, 1}^d, 可以假设log p(x|z; θ) 服从多变量的伯努利分布,即

• x in R^d, 可以假设p(x|z; θ) 服从对角化协方差的高斯分布,即

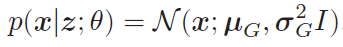
目标：找到一组θ^∗ 来最大化证据下界ELBO(q, x; θ, ϕ)，

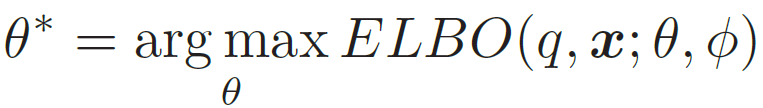
模型

总目标函数

其中先验分布p(z; θ) = N(z|0, I)，θ 和ϕ 分别表示生成网络和推断网络的参数。

训练

可以采用随机梯度方法，每次从数据集中采集一个样本x，然后根据q(z|x; ϕ)采集一个隐变量z，则目标函数为

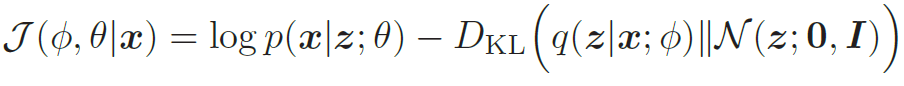
此时，KL 散度可以直接计算出闭式解。对于d 维空间中的两个正态分布N(μ₁,Σ₁) 和N(μ₂,Σ₂)，其KL散度为

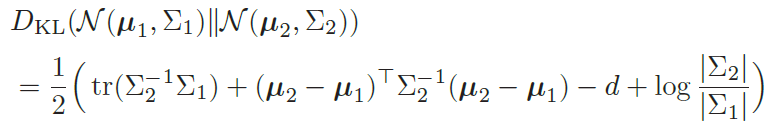
其中tr(·)表示矩阵的迹，| · |表示矩阵的行列式。具体可以看这个链接。

所以，我们有

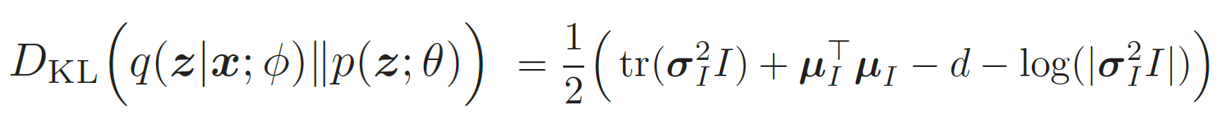
最后，VAE里面有一个非常重要的trick -- Reparameterization

再参数化

问题: 如何求随机变量z 关于参数ϕ 的导数，。因为随机变量z 采样自后验分布q(z|x; ϕ)，和参数ϕ相关。但由于是采样的方式，无法直接刻画z 和ϕ 之间的函数关系，因此也无法计算z 关于ϕ 的导数

假设q(z|x; ϕ) 为正态分布N(μ_I ,σ_I²I)，其中μ_I 和σ_I 是推断网络f_I (x; ϕ) 的输出。我们可以采用下面方式来采样z。

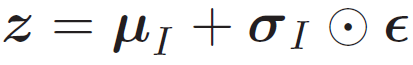
其中ϵ ∼ N(0, I)。这样z 和μ_I ,σ_I 的关系从采样关系变为函数关系，就可以求z关于ϕ 的导数。

通过再参数化，变分自编码器可以通过梯度下降法来学习参数了。如果进一步假设p(x|z; θ) 服从高斯分布N(x|μ_G, I)，其中μ_G = f_G(z; θ) 是生成网络的输出，则目标函数可以简化为

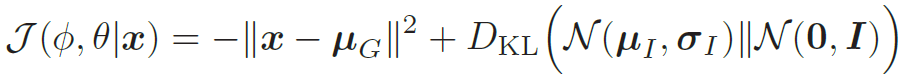
下面是整个变分自编码器的训练过程