BUUCTF--rsa

测试文件：https://buuoj.cn/files/ed10ec009d5aab0050022aee131a7293/41c4e672-98c5-43e5-adf4-49d75db307e4.zip?token=eyJ0ZWFtX2lkIjpudWxsLCJ1c2VyX2lkIjoxOTAzLCJmaWxlX2lkIjoyMDV9.XYl7ag.BZcdhjGojXT726Y0wj4m2X_OOyw

文件分析

第一次遇到这种题，不过看到题目知道这是一个rsa解密题。

公钥n = p * q，其中p和q是两个大素数

e是随机选择的数，作为公钥

d是跟e有关的一个数，满足条件式：ed=1（mod phi（n））

phi（n）是欧拉函数，phi（n）=（p-1）（q-1）

转自：https://blog.csdn.net/kevin66654/article/details/54087647

pub.key是公钥，flag.enc是rsa加密后的文件，因此我们只要通过公钥文件解析出n,e,p,q,d，再利用脚本解密rsa加密文件。

公钥处理

提取公钥

IDA打开pub.key后，转换里面的十六进制为字符串，提取出公钥。

-----BEGIN PUBLIC KEY-----
MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMAzLFxkrkcYL2wch21CM2kQVFpY9++
/AvKr1rzQczdAgMBAAE=
-----END PUBLIC KEY-----

公钥解析(提取e,n)

在http://tool.chacuo.net/cryptrsakeyparse对公钥进行解析

公钥指数及模数信息:

key长度：	256
模数：	C0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD
指数：	65537 (0x10001)

获取到

e = 65537

n=86934482296048119190666062003494800588905656017203025617216654058378322103517(模数转换为十进制)

公钥解析(提取p,q)

使用yahu或者http://www.factordb.com/index.php?query=86934482296048119190666062003494800588905656017203025617216654058378322103517 通过n解析p,q

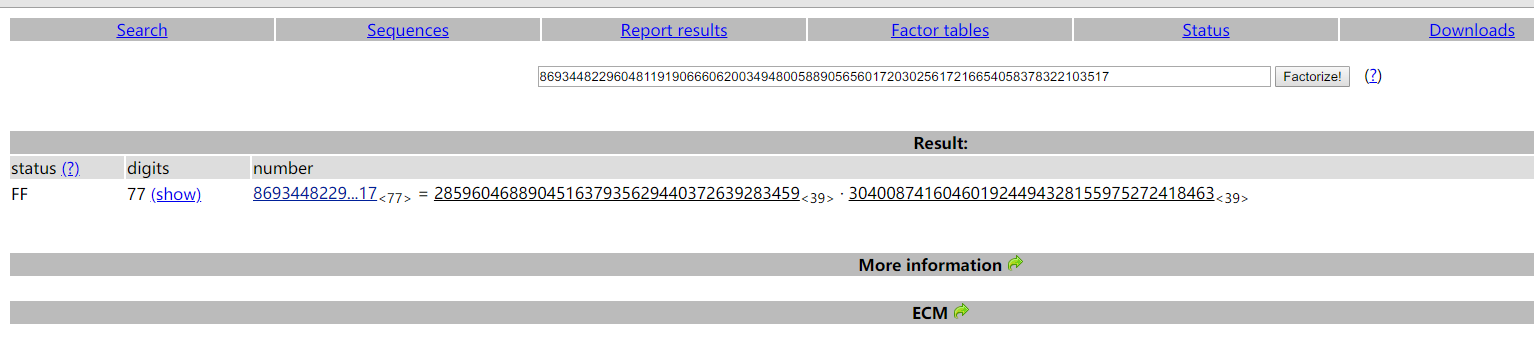
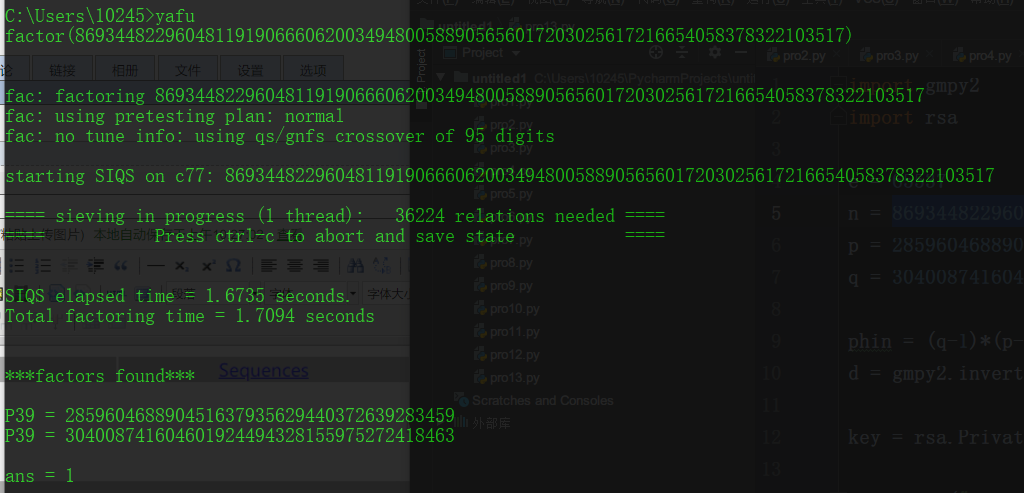
p = 285960468890451637935629440372639283459

q = 304008741604601924494328155975272418463

脚本解密

import gmpy2
import rsa

e = 65537
n = 86934482296048119190666062003494800588905656017203025617216654058378322103517
p = 285960468890451637935629440372639283459
q = 304008741604601924494328155975272418463

phin = (q-1)*(p-1)
d = gmpy2.invert(e, phin)

key = rsa.PrivateKey(n, e, int(d), p, q)

with open("C:\\Users\\10245\\Desktop\\output\\flag.enc", "rb+") as f:
    f = f.read()
    print(rsa.decrypt(f, key))

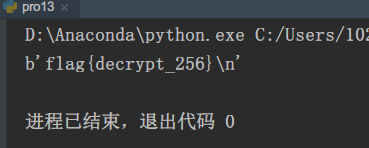
get flag！

flag{decrypt_256}

想要详细了解CTF中的rsa，可以看看https://err0rzz.github.io/2017/11/14/CTF%E4%B8%ADRSA%E5%A5%97%E8%B7%AF/