POJ 3728 The merchant （树形DP+LCA）

题目：https://vjudge.net/contest/323605#problem/E

题意：一棵n个点的树，然后有m个查询，每次查询找(u->v)路径上的两个数，a[i],a[j],（i<j）a[j]-a[i]的最大值，j必须是u->v路径上出现的比i晚

思路：首先我们路径肯定是确定只有一条的，然后我们怎么找出那条路径呢，我们可以求LCA，求出u->LCA（u，v）   LCA(u,v)->v  ，这样我们就能把路径给确定出来

然后我们先简化问题，如果是一个序列，我们要找两个数的最大差值，我们可以维护一个单调栈，然后每次求最大差值，复杂度为O(n)，我们可以先用LCA把路径求出来，然后直接O(n)遍历出来即可，但是查询数量有 <=50000,会超时，这个时候我们只能想能不能预处理一些有用的东西，然后O(1)查询出来，因为LCA复杂度为O(logn)*（O(m)查询数）复杂度正好，我们可以优化上述算法，首先我们肯定和最大值最小值有关，我们求出每个点到LCA的最小值，和LCA到当前点的最大值，然后如何练习起来呢，其实我们可以把路径合并，首先两个点之间间隔一条边，肯定就是max(value[v]-value[u],0),然后合并的时候有一个转移方程，max(u->LCA(u,v)的利润，LCA(u,v)->v的利润，max(LCA(u,v)->v)-min(u,LCA(u,v))   ), 为什么呢下面给出三个例子

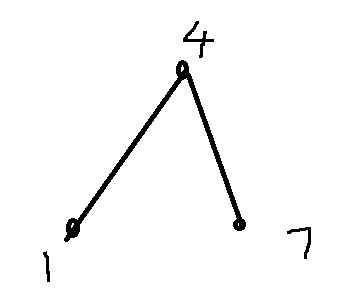
例子一，这个就是用maxvalue-minvalue

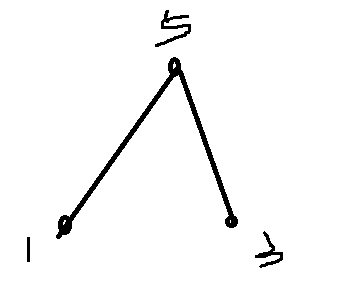
例子二，这个就是u->LCA(u,v)情况

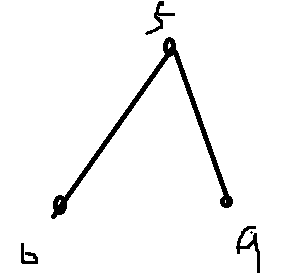
例子三，这个就是LCA（u，v）->v的情况

然后差不多就可以解出来了，因为本人对LCA还不会太操作，然后就没写代码了，发现自己思路是对的，就直接贴别人代码了>_<

来源：https://blog.csdn.net/xingyeyongheng/article/details/20402603

/*分析:先求出点u,v的最近公共祖先f,然后求u->f->v的利润最大值maxval
对于这个maxval可能有三种情况:
1:maxval是u->f的maxval
2:maxval是f->v的maxval
3:maxval是u->f的最小w[i]减去f->v的最大w[i]
分析到这很明显需要设置4个变量来求maxval:
up[u]表示u->f的最大maxval
down[u]表示f->u的最大maxval
maxw[u]表示u-f的最大w[i]
minw[u]表示u-f的最小w[i]
所以maxval=max(max(up[u],down[v]),maxw[v]-minw[u]);
现在问题就是如何快速的求出这四个变量,在这里我们可以对u,v的LCA(u,v)进行分类解决
对于LCA(u,v)是f的询问全部求出,然后再求LCA(u,v)是f的父亲的询问
这样当我们求LCA(u,v)是f的父亲的询问的时候就可以借用已经求出的LCA(u,v)是f的询问
 的结果,这样就不用反复去求u->f的那四个变量值,u->father[f]也能快速求出
 这个变化主要在寻找father[v]这个过程中进行,具体看代码
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <algorithm>
#include <map>
#include <cmath>
#include <iomanip>
#define INF 99999999
typedef long long LL;
using namespace std;

const int MAX=+;
int n,m,size;
int uu[MAX],vv[MAX],ww[MAX],sum[MAX];
int up[MAX],down[MAX],maxw[MAX],minw[MAX],father[MAX];
int head[MAX],head2[MAX],head3[MAX];
bool mark[MAX];

struct Edge{
    int v,id,next;
    Edge(){}
    Edge(int V,int ID,int NEXT):v(V),id(ID),next(NEXT){}
}edge[MAX*],edge2[MAX*],edge3[MAX*];

void Init(int num){
    for(int i=;i<=num;++i)head[i]=head2[i]=head3[i]=-,mark[i]=false;
    size=;
}

void InsertEdge(int u,int v,int id){
    edge[size]=Edge(v,id,head[u]);
    head[u]=size++;
}

void InsertEdge2(int u,int v,int id){
    edge2[size]=Edge(v,id,head2[u]);
    head2[u]=size++;
}

void InsertEdge3(int u,int v,int id){
    edge3[size]=Edge(v,id,head3[u]);
    head3[u]=size++;
}

int findset(int v){
    if(v == father[v])return father[v];
    int fa=father[v];
    father[v]=findset(father[v]);
    up[v]=max(max(up[v],up[fa]),maxw[fa]-minw[v]);
    down[v]=max(max(down[v],down[fa]),maxw[v]-minw[fa]);
    maxw[v]=max(maxw[v],maxw[fa]);
    minw[v]=min(minw[v],minw[fa]);
    return father[v];
}

void LCA(int u){
    mark[u]=true;
    father[u]=u;
    for(int i=head2[u];i != -;i=edge2[i].next){//对LCA(u,v)进行分类
        int v=edge2[i].v,id=edge2[i].id;
        if(!mark[v])continue;
        int f=findset(v);
        InsertEdge3(f,v,id);
    }
    for(int i=head[u];i != -;i=edge[i].next){
        int v=edge[i].v;
        if(mark[v])continue;
        LCA(v);
        father[v]=u;
    }
    for(int i=head3[u];i != -;i=edge3[i].next){
        int id=edge3[i].id;
        findset(uu[id]);
        findset(vv[id]);
        sum[id]=max(max(up[uu[id]],down[vv[id]]),maxw[vv[id]]-minw[uu[id]]);
    }
}

int main(){
    int u,v;
    while(~scanf("%d",&n)){
        Init(n);
        for(int i=;i<=n;++i){
            scanf("%d",ww+i);
            up[i]=down[i]=;
            maxw[i]=minw[i]=ww[i];
        }
        for(int i=;i<n;++i){
            scanf("%d%d",&u,&v);
            InsertEdge(u,v,i);
            InsertEdge(v,u,i);
        }
        size=;
        scanf("%d",&m);
        for(int i=;i<m;++i){
            scanf("%d%d",&uu[i],&vv[i]);
            InsertEdge2(uu[i],vv[i],i);
            InsertEdge2(vv[i],uu[i],i);
        }
        size=;
        LCA();
        for(int i=;i<m;++i)printf("%d\n",sum[i]);
    }
    return ;
}