OSPF与ACL 综合应用

1.企业内网运行OSPF路由协议，区域规划如图所示；
2.财务和研发所在的区域不受其他区域链路不稳定性影响；
3.R1、R2、R3只允许被IT登录管理；
4.YF和CW之间不能互通，但都可以与IT互通；
5.IT和YF可以访问Client1，但CW不能访问Client1；
6.YF和CW只能访问Server1的WWW服务；

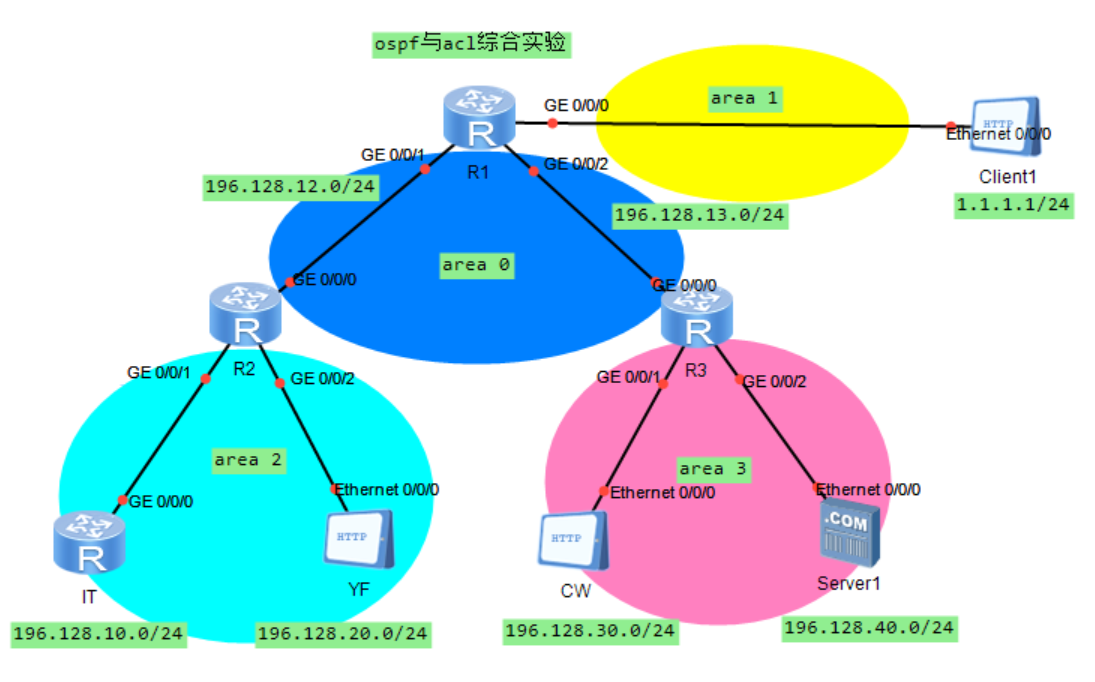
分析：
CW
1.YF和CW之间不能互通，但都可以与IT互通；
2.CW不能访问Client1；
3.CW只能访问Server1的WWW服务；
YF
1.YF和CW之间不能互通，但都可以与IT互通；
3.YF只能访问Server1的WWW服务；
IT
1.R1、R2、R3只允许被IT登录管理；
2.IT可以访问Client1；

一、配置基本网络

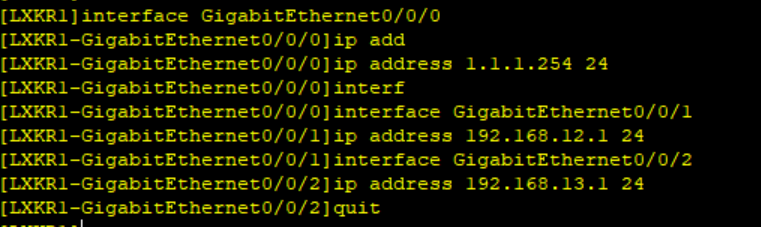
二、配置OSPF

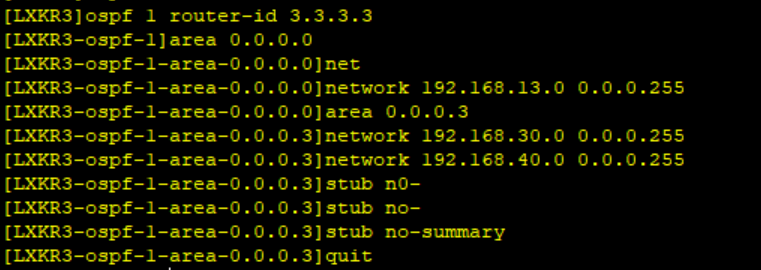
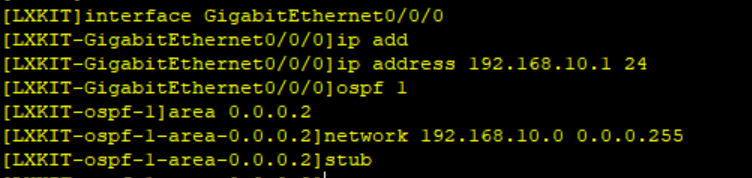
三、配置ACL,，满足企业需求

财务部ACL设置

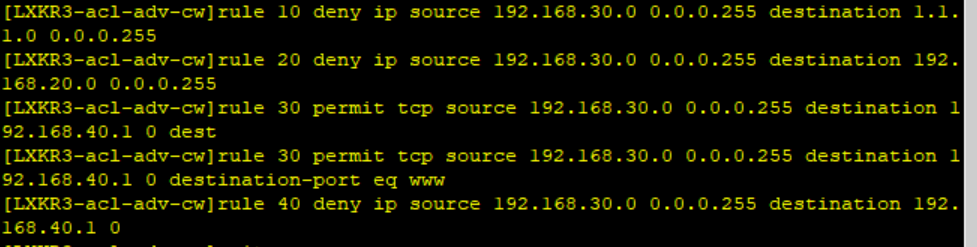
研发部ACL设置

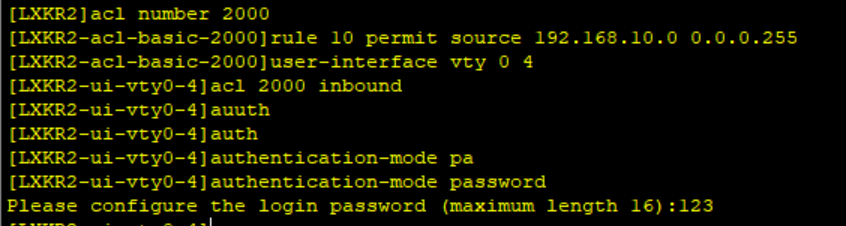
IT部ACL设置

项目验证：
    验证一：在CW网络进行验证，如下
    财务可以访问server1服务器的web服务

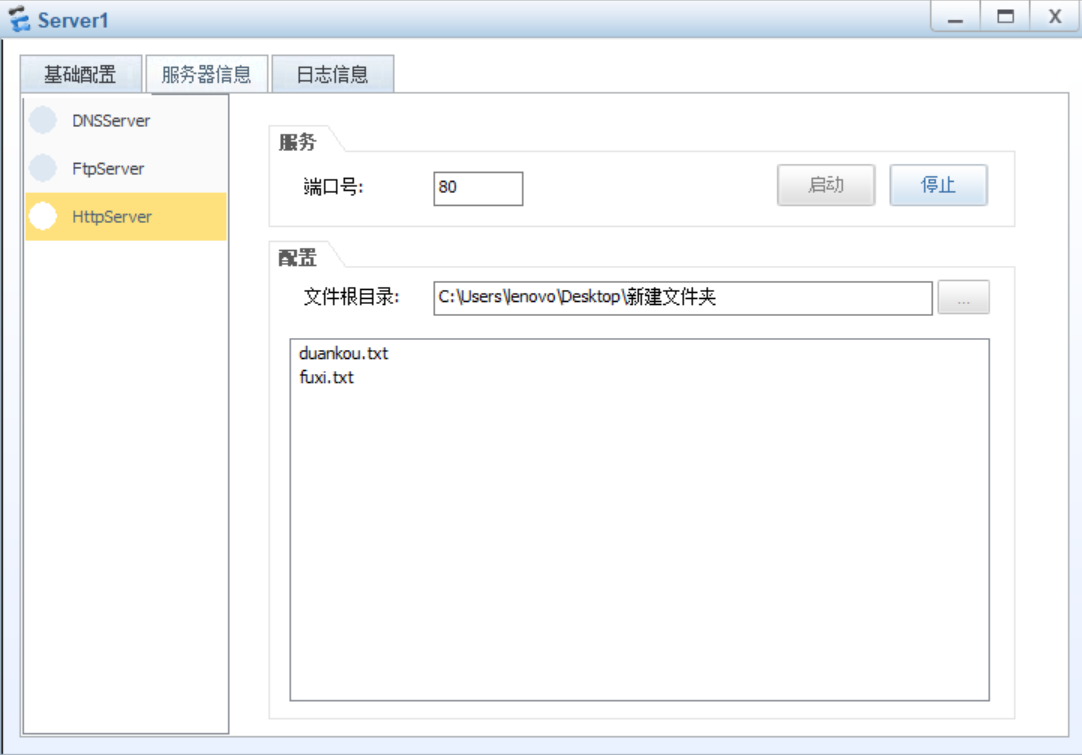
但无法ping通server1服务器

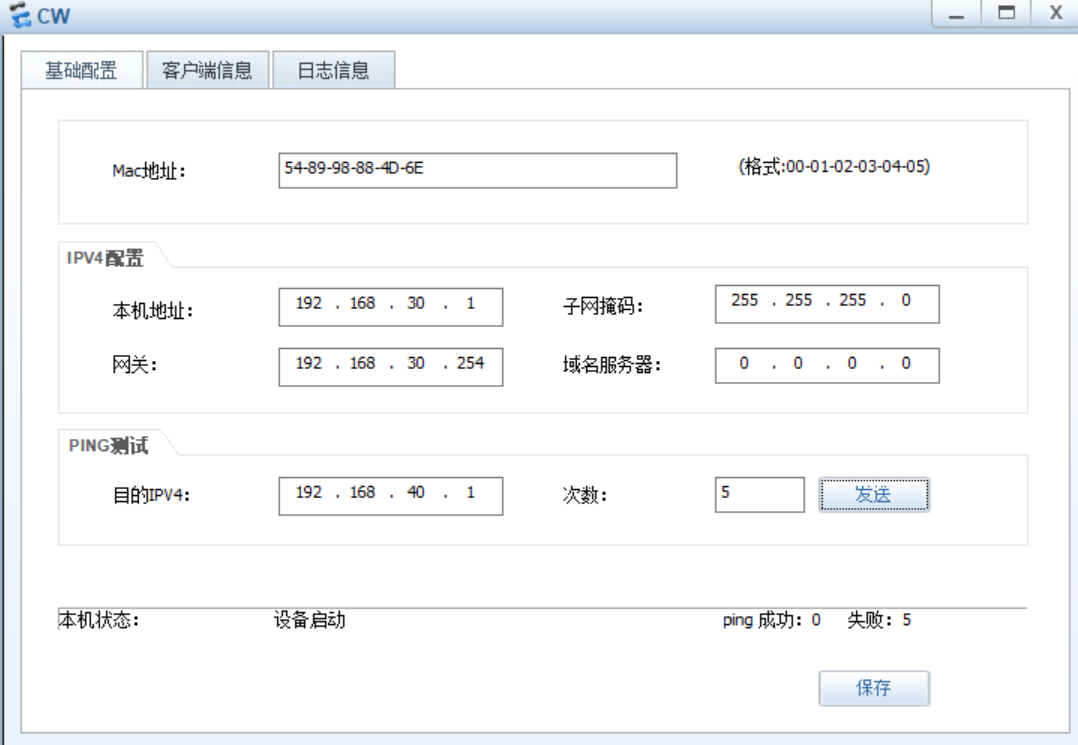
验证二：在YF网络进行验证，如下

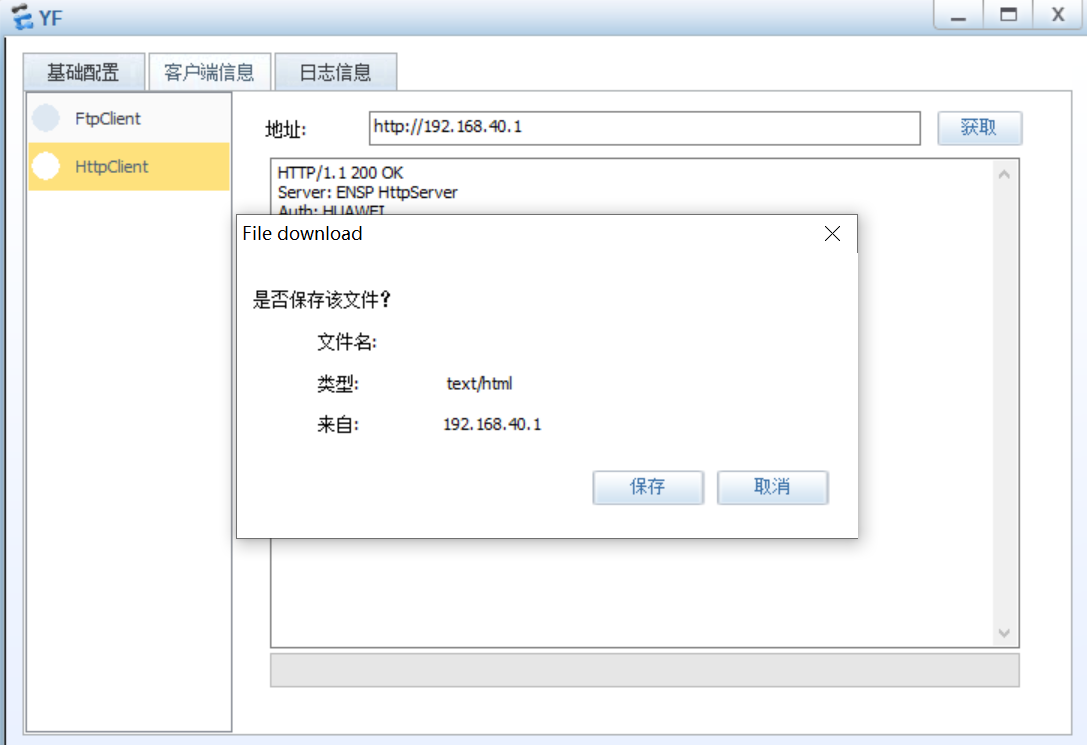
但是无法ping通

验证三：R1、R2、R3只允许被IT登录管理，如下
IT可以登录R2：

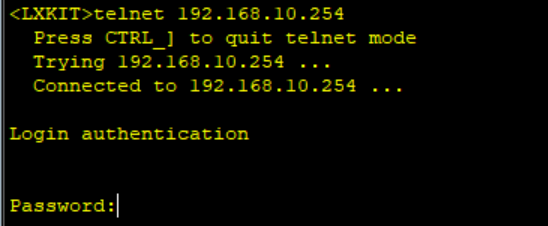
R1不可以登陆R2

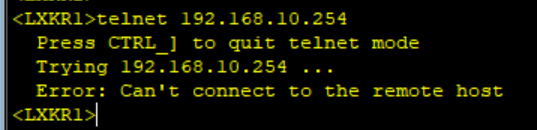
所以项目要求验证成功

        项目总结：
                    1.项目在配置ospf时一定要注意特殊区域的配置要完整；
                    2.在配置acl时要主要序列号和源、目标ip地址配置正确。