Minimum Snap轨迹规划详解（1）轨迹规划

一. 轨迹规划是什么？

在机器人导航过程中，如何控制机器人从A点移动到B点，通常称之为运动规划。运动规划一般又分为两步：

1、路径规划：在地图（栅格地图、四\八叉树、RRT地图等）中搜索一条从A点到B点的路径，由一系列离散的空间点（waypoint）组成。

2、轨迹规划：由于路径点可能比较稀疏、而且不平滑，为了能更好的控制机器人运动，需要将稀疏的路径点变成平滑的曲线或稠密的轨迹点，也就是轨迹。

2. 轨迹是什么？注意低次项在前

轨迹一般用n阶多项式(polynomial)来表示，即

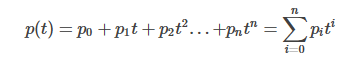
其中p0,p1,...,pn为轨迹参数（n+1个），设参数向量p=[p0,p1,...,pn]T，则轨迹可以写成向量形式。

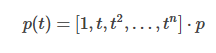
对于任意时刻t，可以根据参数计算出轨迹的位置P(osition)，速度V(elocity)，加速度A(cceleration)，jerk，snap等。

一个多项式曲线过于简单，一段复杂的轨迹很难用一个多项式表示，所以将轨迹按时间分成多段，每段各用一条多项式曲线表示，形如：

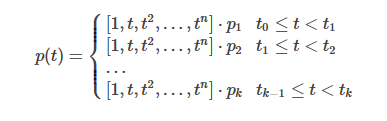
k为轨迹的段数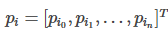，为第i段轨迹的参数向量。

此外，实际问题中的轨迹往往是二维、三维甚至更高维，通常每个维度单独求解轨迹。

3. Minimum Snap轨迹规划

轨迹规划的目的：求轨迹的多项式参数p1,...,pk。
我们可能希望轨迹满足一系列的约束条件，比如：希望设定起点和终点的位置、速度或加速度，希望相邻轨迹连接处平滑（位置连续、速度连续等），希望轨迹经过某些路径点，设定最大速度、最大加速度等，甚至是希望轨迹在规定空间内（Obstruction check）等等。
通常满足约束条件的轨迹有无数条，而实际问题中，往往需要一条特定的轨迹，所以又需要构建一个最优的函数，在可行的轨迹中找出“最优”的那条特定的轨迹。所以，我们将问题建模（fomulate）成一个约束优化问题，形如：

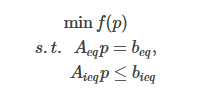
这样，就可以通过最优化的方法求解出目标轨迹参数p。注意：这里的轨迹参数p是多端polynomial组成的大参数向量

我们要做的就是：将优化问题中的f(p)函数和A_e_q,b_e_q,A_i_e_q,b_ieq参数给列出来，然后丢到优化器中求解轨迹参数p。

Minimum Snap顾名思义，Minimum Snap中的最小化目标函数是Snap（加速度的二阶导），当然你也可以最小化Acceleration（加速度）或者Jerk（加速度的导数），至于它们之间有什么区别，quora上有讨论。一般不会最小化速度。

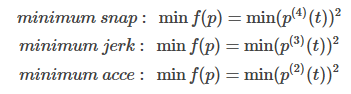
4. 一个简单的例子

给定包含起点终点在内的k+1个二维路径点p_t₀,p_t₁,...,p_t_k，p_t_i=(x_i,y_i)，给定起始速度和加速度为v₀,a₀，末端加速度为v_e,a_e，给定时间T，规划出经过所有路径点的平滑轨迹。

a. 初始轨迹分段与时间分配

根据路径点，将轨迹分为k段，计算每段的距离，按距离平分时间T(匀速时间分配)，得到时间序列t₀,t₁,...,t_k。对x,y维度单独规划轨迹。后面只讨论一个维度。

时间分配的方法：匀速分配或梯形分配，假设每段polynomial内速度满足匀速或梯形速度变化，根据每段的距离将总时间T分配到每段。

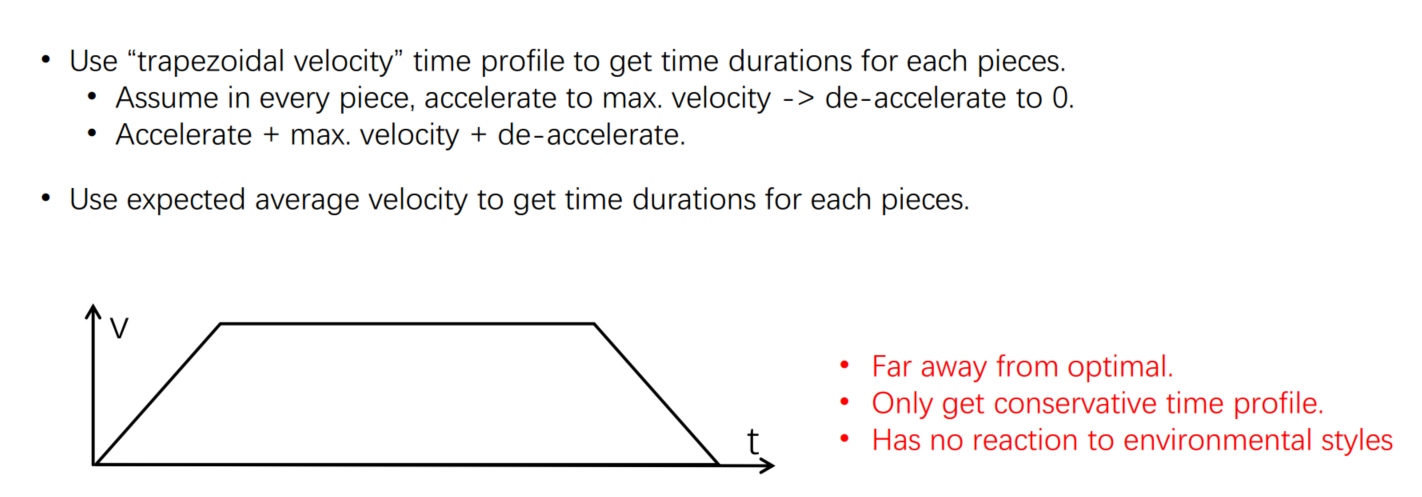
这里的轨迹分段和时间分配都是初始分配，在迭代算法中，如果 Obstruction check和 feasibility check不满足条件，会插点或增大某一段的时间。

b. 构建优化函数

Minimum Snap的优化函数为：

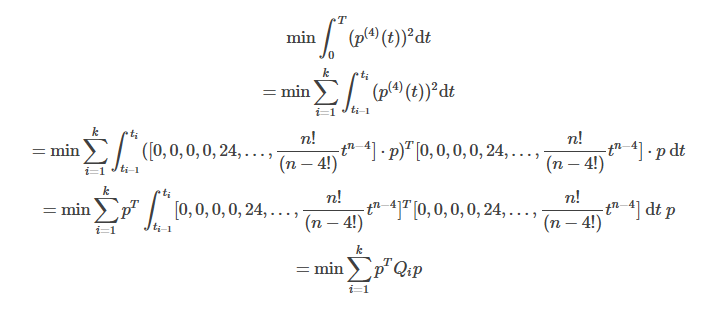
其中，

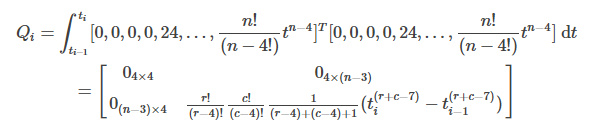
注意：r,c为矩阵的行索引和列索引，索引从0开始，即第一行 r=0。

可以看到，问题建模成了一个数学上的二次规划（Quadratic Programming，QP）问题。

c. 构建等式约束方程

设定某一个点的位置、速度、加速度或者更高为一个特定的值，可以构成一个等式约束。
例如：

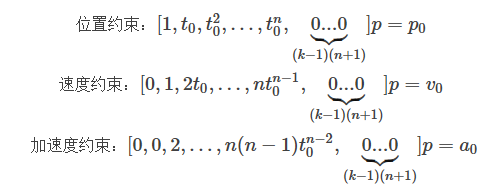
由于要过中间点，对中间点的位置也构建等式约束，方法同上。

2. 相邻段之间的位置、速度、加速度连续可以构成一个等式约束

例如第i、i+1段的位置连续构成的等式约束为

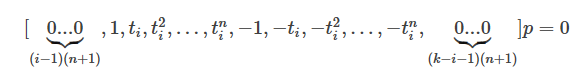
合并所有等式约束，得到

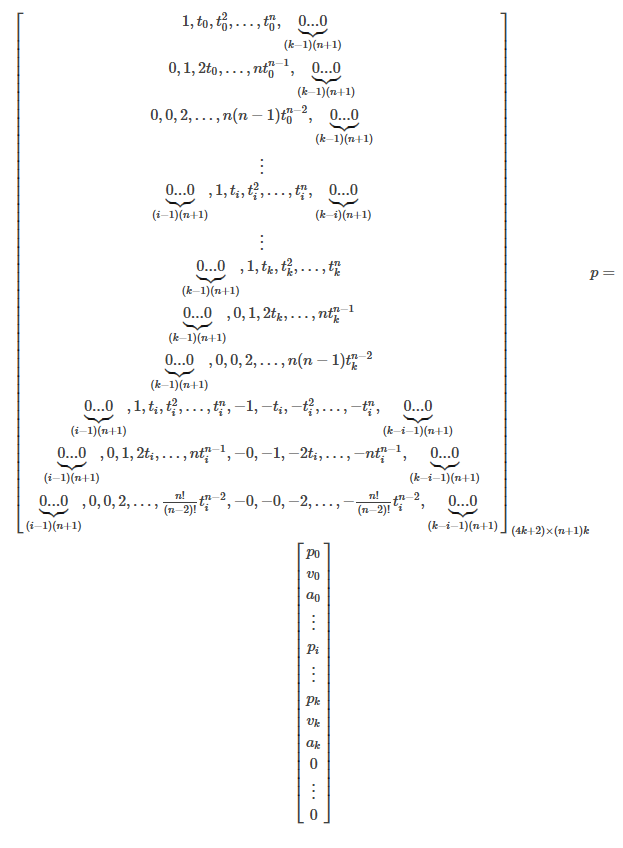
等式约束个数=3（起始PVA）+k-1（中间点的p）+3（终点pva）+3(k-1)（中间点PVA连续）=4k+2。

d. 构建不等式约束

不等式约束与等式约束类似，也是设置某个点的P、V、A小于某一特定值，从而构建Aieqp=bieq

，不等式约束一般是在corridor中用的比较多，这里暂时先不使用不等式约束。

e. 求解

利用QP求解器进行求解，在MATLAB中可以使用quadprog() 函数，C++的QP求解器如OOQP，也可以自己去网上找。

参考资料：

1、深蓝学院

2、https://blog.csdn.net/q597967420/article/details/76099491