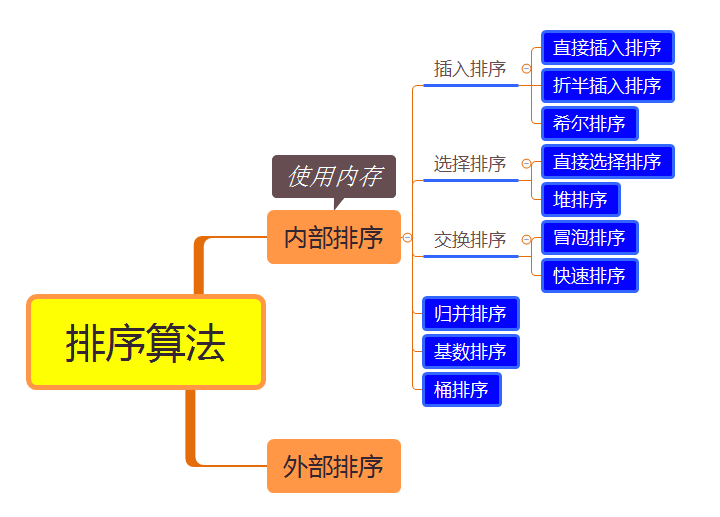
java排序算法概述

一、概述　　

　　1、排序也称排序算法(Sort Algorithm)，排序是将一组数据，依指定的顺序进行排列的过程。

　　2、排序的分类：

　　　　1) 内部排序:

　　　　　　指将需要处理的所有数据都加载到内部存储器中进行排序。

　　　　2) 外部排序法：

　　　　　　数据量过大，无法全部加载到内存中，需要借助外部存储进行排序。

　　　　3)常见算法分类：

　　3、十种算法（蓝色）的时间复杂度

一、算法时间复杂度

　　1、度量一个程序(算法)执行时间的两种方法

　　　　1）事后统计的方法
　　　　这种方法可行, 但是有两个问题：

　　　　一是要想对设计的算法的运行性能进行评测，需要实际运行该程序；

　　　　二是所得时间的统计量依赖于计算机的硬件、软件等环境因素, 这种方式，要在同一台计算机的相同状态下运行，才能比较那个算法速度更快。
　　　　2）事前估算的方法
　　　　通过分析某个算法的时间复杂度来判断哪个算法更优

二、时间频度

　　1）基本介绍

　　时间频度：一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)

　　2）举例说明-忽略常数项

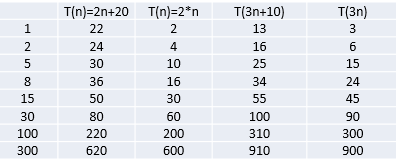
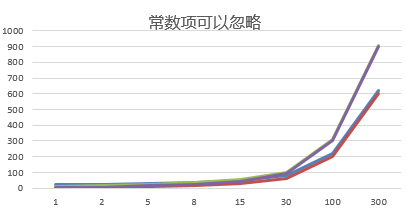
　　结论:
　　2n+20 和 2n 随着n 变大，执行曲线无限接近, 20可以忽略
　　3n+10 和 3n 随着n 变大，执行曲线无限接近, 10可以忽略

　　3）举例说明-忽略低次项

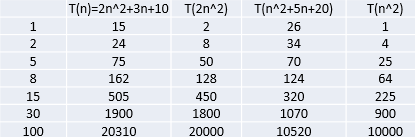
　　结论:
　　2n^2+3n+10 和 2n^2 随着n 变大, 执行曲线无限接近, 可以忽略 3n+10
　　n^2+5n+20 和 n^2 随着n 变大,执行曲线无限接近, 可以忽略 5n+20

　　4）举例说明-忽略系数

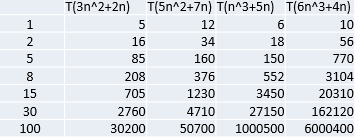
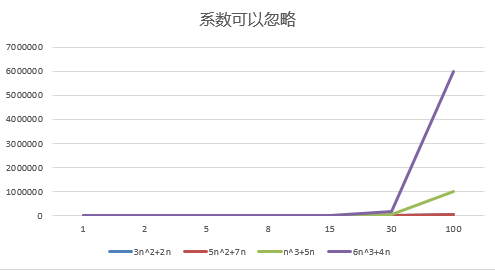
　　结论:
　　随着n值变大，5n^2+7n 和 3n^2 + 2n ，执行曲线重合, 说明这种情况下, 5和3可以忽略。
　　而n^3+5n 和 6n^3+4n ，执行曲线分离，说明多少次方式关键

三、时间复杂度

　　1）一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作 T(n)=Ｏ( f(n) )，称Ｏ( f(n) ) 为算法的渐进时间复杂度，简称时间复杂度。

　　2）T(n) 不同，但时间复杂度可能相同。如：T(n)=n²+7n+6 与 T(n)=3n²+2n+2 它们的T(n) 不同，但时间复杂度相同，都为O(n²)。
　　3）计算时间复杂度的方法：

用常数1代替运行时间中的所有加法常数 T(n)=n²+7n+6 => T(n)=n²+7n+1
修改后的运行次数函数中，只保留最高阶项 T(n)=n²+7n+1 => T(n) = n²
去除最高阶项的系数 T(n) = n² => T(n) = n² => O(n²)

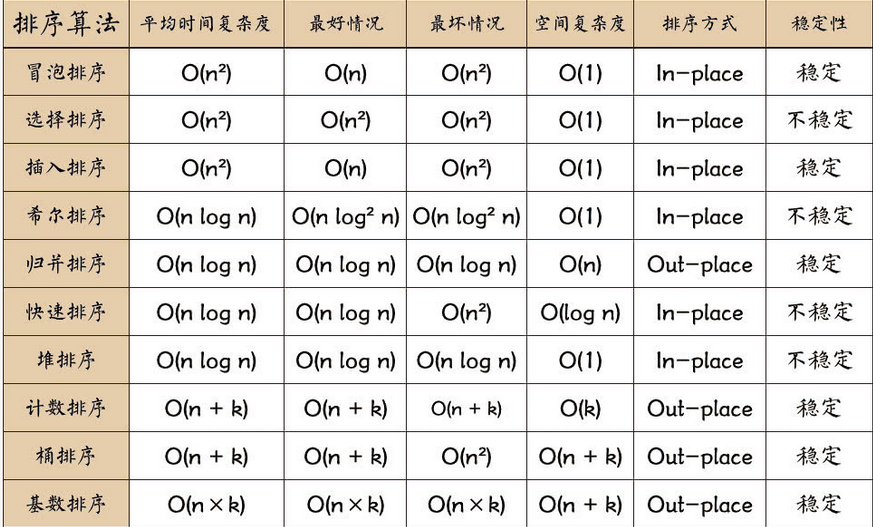
四、常见的时间复杂度

常数阶O(1)
对数阶O(log2n)
线性阶O(n)
线性对数阶O(nlog2n)
平方阶O(n^2)
立方阶O(n^3)
k次方阶O(n^k)
指数阶O(2^n)

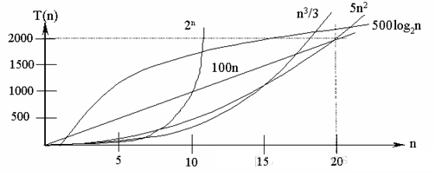
　　说明：

　　常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜ Ο(nk) ＜Ο(2n) ，随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低
　　从图中可见，我们应该尽可能避免使用指数阶的算法

　　1）常数阶O(1)

　　无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)

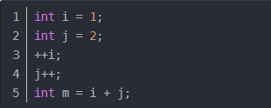
　　上述代码在执行的时候，它消耗的时候并不随着某个变量的增长而增长，那么无论这类代码有多长，即使有几万几十万行，都可以用O(1)来表示它的时间复杂度。
　　2）对数阶O(log₂n)

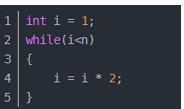
　　说明：

　　在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近了。假设循环x次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n，那么 x = log2n也就是说当循环 log2n 次以后，这个代码就结束了。因此这个代码的时间复杂度为：O(log₂n) 。 O(log₂n) 的这个2 时间上是根据代码变化的，i = i * 3 ，则是 O(log₃n)
　　

　　3）线性阶O(n)

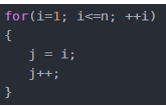
　　说明：

　　这段代码，for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的，因此这类代码都可以用O(n)来表示它的时间复杂度
　　4）现行对数阶O(nlogN)

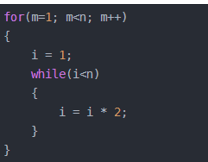
　　说明：

　　线性对数阶O(nlogN) 其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)
　　5）平方阶O(n²)

　　说明：

　　平方阶O(n²) 就更容易理解了，如果把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 O(n²)，这段代码其实就是嵌套了2层n循环，它的时间复杂度就是 O(n*n)，即 O(n²) 如果将其中一层循环的n改成m，那它的时间复杂度就变成了 O(m*n)
　　6）立方阶O(n³)、K次方阶O(n^k)

　　说明：

　　参考上面的O(n²) 去理解就好了，O(n³)相当于三层n循环，其它的类似

五、空间复杂度

　　基本介绍

　　1、类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间，它也是问题规模n的函数。
　　2、空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况
　　3、在做算法分析时，主要讨论的是时间复杂度。从用户使用体验上看，更看重的程序执行的速度。一些缓存产品(redis, memcache)和算法(基数排序)本质就是用空间换时间.

六、相关术语

　　1）稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
　　2）不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
　　3）内排序：所有排序操作都在内存中完成；
　　4）外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
　　5）时间复杂度：一个算法执行所耗费的时间。
　　6）空间复杂度：运行完一个程序所需内存的大小。
　　7）n: 数据规模
　　8）k: “桶”的个数
　　9）In-place: 不占用额外内存
　　10）Out-place: 占用额外内存