ICPC2019上海区域赛 部分题解(正在更新)

K. Color Graph

题意:

给定一个简单图，点个数<=16，删去部分边后，使得该图中无边数为奇数得环，问剩下的边数最大为多少？

思路:

如果一个图中无奇数边的环，那么这个图一定是个二分图。只要枚举二分图的左部，统计所有从左部到右部的边个数，答案就是枚举出的所有边数的最大值。(因为最优解一定也是一个二分图，所以一定会被枚举到)

//赛后补题，只过样例，仅供参考
#include <bits/stdc++.h>
using namespace std;
const int maxn=105;
const int maxm=1e4+5;
struct edge{
    int u,v;
}E[maxm];
int tot=0;
void addedge(int u,int v){
    E[++tot].u=u;
    E[tot].v=v;
}
int color[maxn];
int main(){
    int T;
    cin>>T;
    for(int kase=1;kase<=T;kase++){
        int n,m;
        scanf("%d%d",&n,&m);
        fill(color,color+1+n,0);
        tot=0;
        for(int i=1;i<=m;i++){
            int u,v;
            scanf("%d%d",&u,&v);
            addedge(u,v);
        }
        int ans=0;
        for(int meijv=0;meijv<=(1<<n)-1;meijv++){
            int mj=meijv;
            for(int i=1;i<=n;i++){
                if(mj&1){
                    color[i]=1;
                }
                else color[i]=0;
                mj>>=1;
            }
            int res=0;
            for(int i=1;i<=tot;i++){
                if(color[E[i].u]!=color[E[i].v]){
                    res++;
                }
            }
            ans=max(ans,res);
        }
        printf("Case #%d: %d\n",kase,ans);
    }
}

---

D. Spanning Tree Removal

题意:

给定一个n阶的完全图，每次操作是从图中移除一棵生成树的所有边，问最多能进行多少次这样的操作？输出操作次数和每次移除的生成树的边。

思路:

n阶完全图共有n*(n-1)/2条边，一棵生成树有n-1条边，很容易猜到能进行n/2次操作，接下来就是如何构造的问题。

下面给出一种直接构造的方法(奇数就孤立出一个点随便连即可)

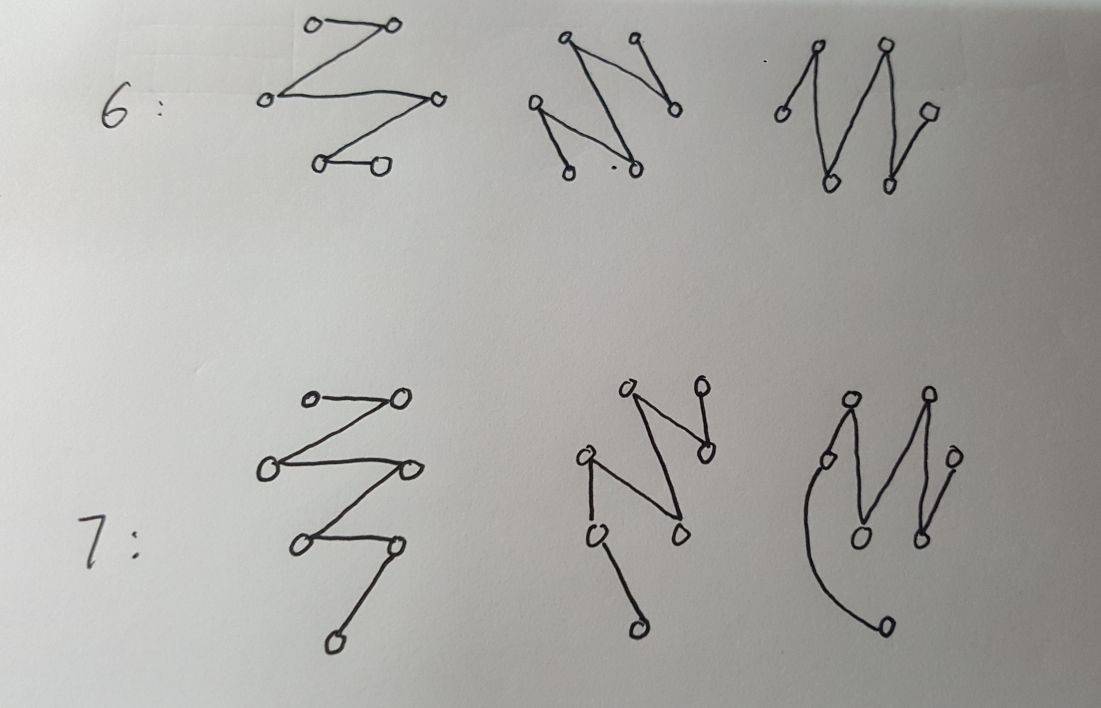
//赛后补题，只过样例，仅供参考
#include <bits/stdc++.h>
using namespace std;
int main(){
    int T;
    cin>>T;
    for(int kase=1;kase<=T;kase++){
        int n;
        scanf("%d",&n);
        printf("Case #%d: %d\n",kase,n/2);
        if(n%2==0){
            for(int i=1;i<=n/2;i++){
                printf("%d %d\n",i,i+1);
                for(int j=1;j<=n/2-1;j++){
                    int u=i+j;
                    int v=(u+n-j*2-1)%n+1;
                    printf("%d %d\n",u,v);
                    printf("%d %d\n",v,u+1);
                }
            }
        }
        else{
            n--;
            for(int i=1;i<=n/2;i++){
                printf("%d %d\n",i,i+1);
                for(int j=1;j<=n/2-1;j++){
                    int u=i+j;
                    int v=(u+n-j*2-1)%n+1;
                    printf("%d %d\n",u,v);
                    printf("%d %d\n",v,u+1);
                }
                printf("%d %d\n",i,n+1);
            }
        }
    }
}

---

H. Tree Partition

题意:

给出一棵点权树，一个树的大小定义为所有点的权值和。问将一棵树分为k棵子树，如何分割才能使所有树的大小的最大值最小？

思路:

二分答案，已知最大连通子图的大小x后，只要在树上从树根向上dp子树的大小即可。如果一个子树u的大小大于x，则先选择u最大的儿子v切除(即切割边u,v)，这样能保证剩下的部分大小尽可能地小。这样保证了图上所有的连通子图的都是小于x的，同时也是用贪心的方法选择切割方案(每个子树都尽可能地取到最大，使剩下部分尽可能小)，得到的就是最小的切割次数。

实现方法：若判断发现一个节点u的权值大于x，则将他的儿子节点排序，从大到小依次删除，直到u的权值小于x。

//赛后还原，仅供参考
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+5;
struct edge{
    int v,next;
}E[maxn];
int head[maxn],tot;
void addedge(int u,int v){
    E[++tot].v=v;
    E[tot].next=head[u];
    head[u]=tot;
}
ll a[maxn],sum[maxn];
int flag=0,cnt;
int n,k;
void dfs(int u,int fa,ll x){
    sum[u]=a[u];
    if(sum[u]>x||flag==0){
        flag=0;
        return;
    }
    for(int i=head[u];i;i=E[i].next){
        int v=E[i].v;
        if(v!=fa){
            dfs(v,u,x);
            sum[u]+=sum[v];
        }
    }
    if(sum[u]>x){
        vector<ll>V;
        for(int i=head[u];i;i=E[i].next){
            int v=E[i].v;
            if(v!=fa){
                V.push_back(sum[v]);
            }
        }
        sort(V.begin(),V.end());
        while(sum[u]>x){
            cnt++;
            sum[u]-=V.back();
            V.pop_back();
        }
    }
    if(cnt>k-1){
        flag=0;
        return;
    }
}
bool check(ll x){
    flag=1;cnt=0;
    dfs(1,0,x);
//    printf("%lld:%d\n",x,flag);
    if(flag)
        return 1;
    else
        return 0;
}
int main(){
    int T;
    cin>>T;
    for(int kase=1;kase<=T;kase++){
        scanf("%d%d",&n,&k);
        fill(head,head+1+n,0);
        fill(sum,sum+1+n,0);
        tot=0;
        for(int i=1;i<=n-1;i++){
            int u,v;
            scanf("%d%d",&u,&v);
            addedge(u,v);
            addedge(v,u);
        }
        for(int i=1;i<=n;i++){
            scanf("%lld",&a[i]);
        }
        ll l=0,r=1e14+5;//左开右闭
        while(r-l>1){
            ll mid=(r+l+1)/2;
            if(check(mid))
                r=mid;
            else
                l=mid;
        }
        printf("Case #%d: %lld\n",kase,r);
    }
}

---

E. Cave Escape

题意:

给定一个\(n * m\)的格子矩阵，其中有一个格子是起点，一个格子是终点。从起点开始移动，每次能移动到有相邻边的格子中，每个格子都有一个权值v,若从点a移动到点b，且b点未被访问过，则可以获得\(Va*Vb\)的收益，若移动到终点，可以选择先不出去，继续在图上乱走，问如何可以使得走出终点后获得得收益最大？(只需要输出最大收益即可)

思路:

很显然终点在哪是对答案完全没有影响的，只要在矩阵中乱走获得最大收益再出去即可。

我们可以将这个矩阵转化为一个无向图，图中的点就是矩阵的格点，相邻格点之间有一条边，长度为它们权值的乘积。只要在这个图上跑一遍最大生成树，树的大小就是最大收益。为什么起点也是对答案没有影响？因为要达到最大收益，最好的方法就是将图中每一个都遍历一遍，因为多遍历一个点是不会亏的，可以通过已经遍历到的任意点往新的点走来得到收益(已经遍历过的格子在矩阵中是连通的，可以到处转移)，这不就是生成树吗？

//赛后补题，只过样例，仅供参考
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e3+5;
const int maxm=4e6+5;
struct edge{
    int u,v;
    ll w;
}E[maxm];
bool cmp(edge a,edge b){
    return a.w>b.w;
}
int tot=0;
void addedge(int u,int v,ll w){
    E[++tot].u=u;
    E[tot].v=v;
    E[tot].w=w;
}
int fa[maxn*maxn];
int n,m;
int find(int x){
    return x==fa[x]?x:fa[x]=find(fa[x]);
}
ll kruskal(){
    for(int i=1;i<=n*m;i++){
        fa[i]=i;
    }
    sort(E+1,E+1+tot,cmp);
    int cnt=0;
    ll ans=0;
    for(int i=1;i<=tot;i++){
        int u=E[i].u;
        int v=E[i].v;
        int fu=find(u);
        int fv=find(v);
        if(fu!=fv){
            fa[fu]=fv;
            ans+=E[i].w;
            cnt++;
        }
        if(cnt==n*m-1)return ans;
    }
}
ll x[maxn*maxn];
ll V[maxn][maxn];
int xx[]={1,0,0,-1};
int yy[]={0,1,-1,0};
int main(){
    int T;
    cin>>T;
    for(int kase=1;kase<=T;kase++){
        int sr,sc,tr,tc;
        scanf("%d%d%d%d%d%d",&n,&m,&sr,&sc,&tr,&tc);
        tot=0;
        ll A,B,C,P;
        scanf("%lld%lld%lld%lld%lld%lld",&x[1],&x[2],&A,&B,&C,&P);
        for(int i=3;i<=n*m;i++){
            x[i]=(x[i-1]*A+x[i-2]*B+C)%P;
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                V[i][j]=x[(i-1)*m+j];
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                for(int pp=0;pp<4;pp++){
                    int it=i+xx[pp];
                    int jt=j+yy[pp];
                    int u=(i-1)*m+j;
                    int v=(it-1)*m+jt;
                    if(it>=1&&it<=n&&jt>=1&&jt<=m){
                        addedge(u,v,V[i][j]*V[it][jt]);
                    }
                }
            }
        }
        ll ans=kruskal();
        printf("Case #%d: %lld\n",kase,ans);
    }
}

---

B. Prefix Code

题意:

给出一系列数字，长度均小于10，问是否有一个数是其他数的前缀？

思路:

Trie树模板题。记录单词的终末，前缀包含的单词个数即可。若一个点是单词终末且前缀包含单词个数>1，则输出No。

//输入字串用s+1，函数调用用s
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int T[maxn][12];
int num[maxn];
int isend[maxn];
int tot=1;
void add(char *s){
    int l=strlen(s+1);
    int rt=1;
    for(int i=1;i<=l;i++){
        if(T[rt][s[i]-'0']==0){
            T[rt][s[i]-'0']=++tot;
            rt=tot;
        }
        else{
            rt=T[rt][s[i]-'0'];
        }
        num[rt]++;
    }
    isend[rt]=1;
}
void init(){
    for(int i=0;i<=tot;i++){
        memset(T[i],0,sizeof(T[i]));
        num[i]=isend[i]=0;
    }
    tot=1;
}
char s[15];
int main(){
    int T;
    cin>>T;
    for(int kase=1;kase<=T;kase++){
        init();
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++){
            scanf("%s",s+1);
            add(s);
        }
        int flag=1;
        for(int i=1;i<=tot;i++){
            if(isend[i]&&num[i]>1){
                flag=0;
                break;
            }
        }
        if(flag)
            printf("Case #%d: Yes\n",kase);
        else
            printf("Case #%d: No\n",kase);
    }
}