dp培训完结(8.9)

概率与期望dp

期望：

为什么下面的式子成立？

若x可以取1,2,3,则x+c可以取1+c,2+c,3+c..........x*c可以取1*c,2*c,3*c

why?

举个例子（E(x+y)=E(x)+E(y)）

如果我们有两个个四面的色子，要计算E(x+y)

第一个色子的取值  1 2 3 4

第二个色子的取值  1 2 3 4

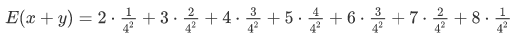
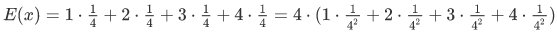
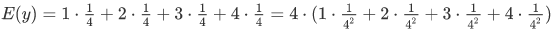
当x+y取值为4时

x的取值：1,2,3

y的取值：1,2,3

所以只考虑4,就有三组互相搭配

也就是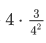

严谨证明：莫得证明

E(x+y)=E(x)+E(y)在任何时候都成立（就算不独立也成立)

注意只有互相独立的时候才能乘起来

概率：求方案数的计数问题

期望：求价值总和的计数问题

（求差）

至少抽一次，有3/4的概率回到最开始的局面，所以是1+x*3/4

bzoj1867

感觉可以从上往下递推？？？

如果不考虑去掉钉子，辣么dp[i][j]=dp[i-1][j-1]*1/2+dp[i-1][j]*1/2(这里j就是按照三角形来的qwq)

那怎么处理没有钉子的情况？

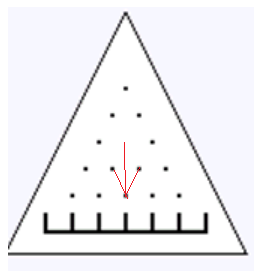
如果(i,j)的上方(i-2)(j-1)没有钉子，那就多了一个从(i-2)(j-1)转移过来

bzoj5004

如果我们打开一个箱子，那么我们可以用箱子里的钥匙去打开其他箱子。

如果由钥匙所处的箱子向该钥匙能打开的箱子建边，就会出现好几个环

那dp[i][j]表示前i个环，选了j个箱子的方案数

dp[i+1][j+k]=dp[i][j]+

bzoj 5091

这里要用到E(x+y)=E(x)+E(y)的性质

答案就是E(x1+x2+...+xn)，其中xi表示是否在第i棵苹果树下

即

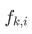表示第k轮到i的概率

震惊！！！

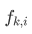竟然是一样的！！！

why???

每个点i接受多少条相邻的边，就有多少个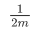,所以总量还是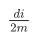

神tm炉石

f[i][a][b][c]:还剩下i轮，血量为1的奴隶的数量为a，血量为2的奴隶数量为b，血量为3的奴隶的数量为c，英雄扣的血的期望

1/s,a/s,b/s,c/s为打到某种人的概率

打到英雄：f[i][a][b][c]--->f[i-1][a][b][c]-1

打到a: f[i][a][b][c]--->f[i-1][a-1][b][看加不加]

打到b：f[i][a][b][c]->f[i-1][a+1][b-1][c]

打到c: f[i][a][b][c]---->f[i-1][a][b+1][c-1]

dp方程大概

（from lz）

换教室

弗洛伊德搞最短路径（求任意两点的最短路径）

dp[i][j]表示前i门课，申请了j门的期望

可以吗？

考虑转移

一门课要么申请要么不申请

不申请：dp[i][j]=dp[i-1][j]

好像要加个距离

距离怎么表示呢？

好像和上一个申不申请有关诶

那就再来一维

dp[i][j][0/1]，记录第i次申不申请

①：若上一次申请，这次不申请：距离=成功概率*成功距离+失败概率*失败距离

②：上一次不申请，这一次申请：同上

③：都不申请：原距离

④：都申请：成功1概率*失败2概率*距离（成功1，失败2）+成功1概率*成功2概率*距离（成功1，成功2）+......

(考虑上一个是否成功，这一个是否成功)

dp[i][j][0]=min(dp[i-1][j][0]+dis(a[i-1],a[i]),dp[i-1][j-1][1]+dis(b[i-1],a[i])*成功概率+dis(a[i-1],a[i])*失败概率)

dp[i][j][1]=min(dp[i-1][j][0]+dis(a[i-1],a[i])*这次失败概率+dis(a[i-1],b[i])*这次成功概率，dp[i-1][j-1][1]+dis(b[i-1],b[i])*上次成功概率*这次成功概率+dis(b[i-1],a[i])*上次成功概率*这次失败概率+dis(a[i-1],b[i])*上次失败概率*这次成功概率+dis(a[i-1],a[i])*上次失败概率*这次成功概率)

妈耶这可真长

bzoj1076奖励关

dp[i][s]表示还剩下i轮游戏，之前吃了s的宝物的期望得分

选择吃或不吃中较大的那个情况

吃：转移到dp[i-1][s(s满足si)]+分数

不吃：转移到dp[i-1][s]

dp[i][s]=max{dp[i-1][s],dp[i-1][s|k]+p[k])/m

为什么要/m呢？

因为每个宝物都有1/m的概率被抛出来

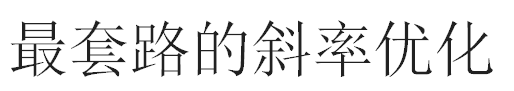
区间dp枚举断点qwq

dp[i]=min{dp[j]+(sum[i]-sum[j])²+M}

然后T飞

斜率优化：

设k<j,j比k要优

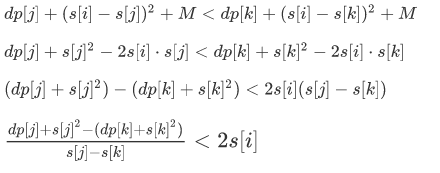
那我们把看做点

两个点的关系：

如果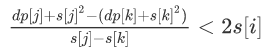,j比k优，反之k比j优

三个点的情况：

设y[j]=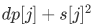

①：2s[i]> 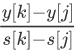>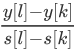:k比j优，l比k优，所以l最优

②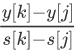：   >2s[i]> 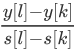:j比k优，l比k优，l和j谁更优不知道，但k肯定没有什么用

③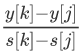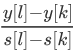：>  > 2s[i]:j比k优，k比l优，所以j最优

总结：反正k不是最优的（可怜的kQnQ）

k是在斜率递减时的中间点，所以我们可以知道：

当斜率递减时，分界点一定不是最优解

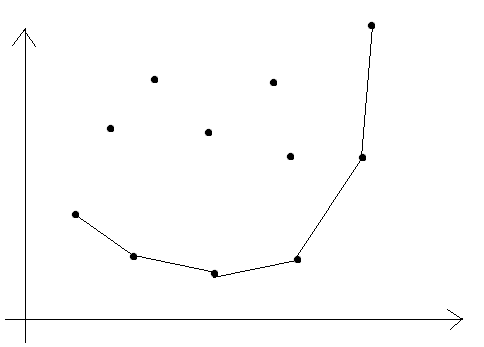
有用的一般是底下的点

注意图中的有线的部分的斜率都是递增的

据说介个东西叫做下凸包

为什么哪些没有划线的点一定不是最优解呢？

我们用下面的点连一下没有线的点，一定可以连出来一个三角形，也就是会出现斜率递减的情况。且斜率递减的交界点就是没有线的点，所以这些没有线的点很没用

维护队首最优

如果发现新加进去的点构成了斜率递减的三元组，则删掉中间的点

斜率优化推式子：

把平方拆开

能消的消掉

把与i相关的放在右边，与j,k相关的放在左边

与j有关的用括号括起来，与k有关的用另一个括号括起来

代码

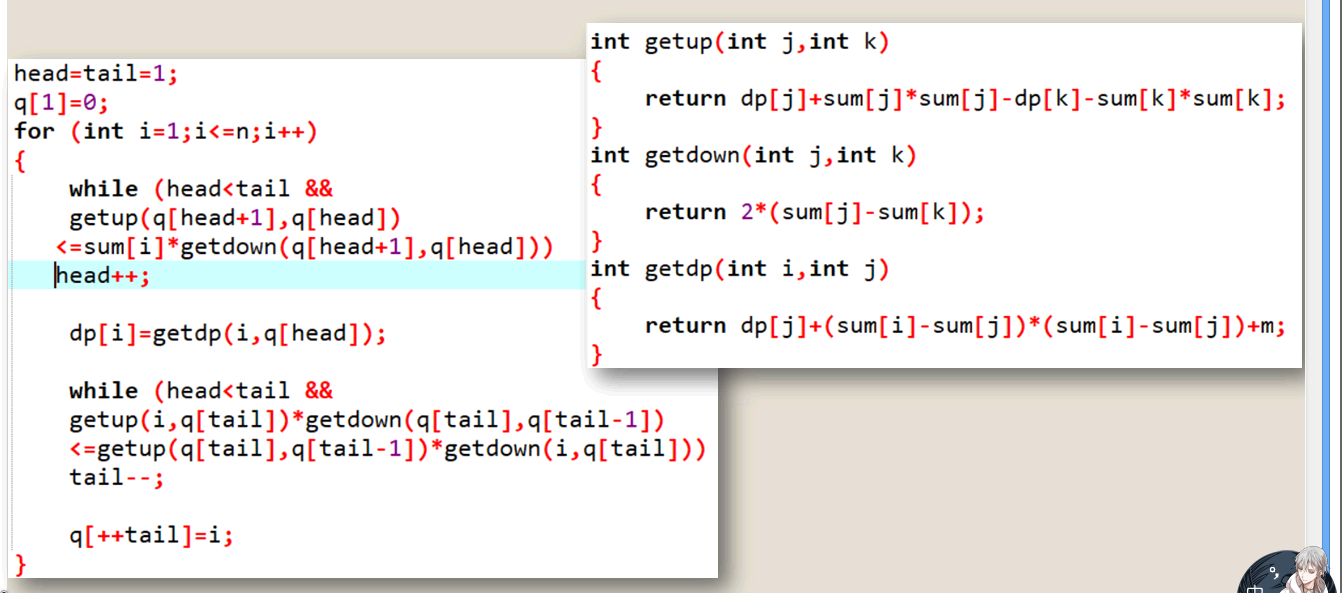
bzoj 4321

1~n考虑不断往里面插

f[i][0/1]前i个，有j个相邻对

如果i+1插在i旁边，则相邻对+1

若插在相邻对之间，相邻对-1

插在其它中间：不变

若i,i-1相邻：i+1插中间不变

总方案数：π(c[i][j]+1)

设f[s]为s集合的点的合法方案数

连通数=随意连-不连通的方案数

既然s不连通，那么站在1号点的角度考虑，1号点肯定会自己分出去一个联通块

枚举1号点分出去的连通块

设1号点连通了t集合，设all[i]位i集合的随意连的方案数（i集合与别的集合之间的边不考虑）

那么all[s^t]也就不考虑s^t和t集合之间的连边了，所以它们并起来就是不连通的，也就是s集合的不合法情况

s不能连通的方案数：s^t总方案数*能连通的方案数

所以就是f[s]=all[s]-(∑all[s^t]*f[t])(t为s的子集且包含s的最后一位)