算法学习记录-查找——平衡二叉树（AVL）

排序二叉树对于我们寻找无序序列中的元素的效率有了大大的提高。查找的最差情况是树的高度。这里就有问题了，将无序数列转化为

二叉排序树的时候，树的结构是非常依赖无序序列的顺序，这样会出现极端的情况。

【如图1】：

　　这样的一颗二叉排序树就是一颗比较极端的情况。我们在查找时候，效率依赖树的高度，所以不希望这样极端情况出现，而是希望元素比较均匀

的分布在根节点两端。

技术参考：fun4257.com/

---

问题提出：

　　能不能有一种方法，使得我们的二叉排序树不依赖无序序列的顺序，也能使得我们得到的二叉排序树是比较均匀的分布。

引入：

　　平衡二叉树（Self-Balancing Binary Search Tree 或 Height-Balanced Binary Search Tree），是一种特殊的二叉排序树，其中每一个结点的

左子树和右子树的高度差至多等于1.

　　这里的平衡从名字中可以看出，Height-Balanced是高度平衡。

　　它或者是一颗空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1.

　　若将二叉树上的结点的平衡因子BF（Balance Factor）定义为该节点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有结点的平衡因子只

可能是-1、0、1。否则就不是平衡二叉树。

　　上图图1中，就不是平衡二叉树。

　　以图1来看看各个结点的平衡因子。

【如下图2】：

---

 技术参考：fun1404.com

如何构成平衡二叉树？

从转化为平衡二叉树的过程中可以提炼出转化的几个基本情况：

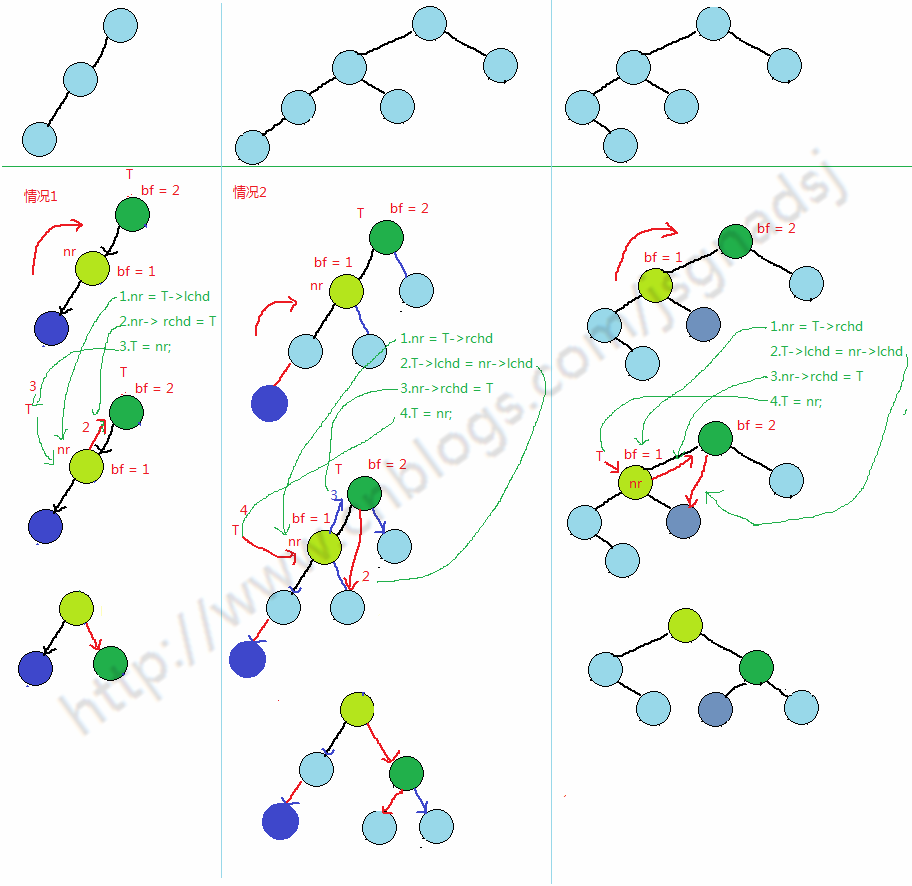
下图是在维基百科上摘录的：

可以看出调整的操作分两大类，前两个是一组，后两个是一组，每组之间是对称的。

前两个是对应上图1 2 中情况，

后两个是对应上图5 6 中情况。

分别以其中一种旋转为例，另一种对应的旋转对称。

单次左旋：对应上图1（左左）中情况

简单左右旋转代码：（只有一次）

 void rotateL(pBinTree *p)//左旋转
 {
     pBinTree r;
     r = (*p)->rchd; //r 为新的根
     (*p)->rchd = r->lchd;
     r->lchd = (*p);
    (*p) = r;
 } 

 void rotateR(pBinTree *p)//右旋转
 {
     pBinTree r;
     r = (*p)->lchd; //r 为新的根

     (*p)->lchd = r->rchd; //新根节点的右孩子附到旧的根结点的左孩子
     r->rchd = (*p);
     (*p) = r;
}

两次旋转 对应图中3（左右）情况

需要旋转两次简单的左右旋转。基于上面代码就可以实现。

为了方便，AVL引入了BF（平衡因子）来调整树。只要出现非平衡树就调整，把不平衡消除最小的情况。

下面就是通过判断BF来实现调整

  void BlanceLeft(pBinTree *p)//从最小非平衡树开始调整
 {
     pBinTree nR,nRchd;
     nR = (*p)->lchd;
      switch (nR->bf)
     {
        case LH:    //新插入的结点在左子树
         {
             (*p)->bf = EH;
             nR->bf = EH;
             rotateR(p);
             break;
        }
         case RH:    //新插入的结点在右子树
         {
             nRchd = nR->rchd;
             switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子？
             {
                 case LH://
                 {
                    (*p)->bf = RH;
                     nR->bf = EH;
                     break;
                }
                 case EH://
                 {
                     (*p)->bf = EH;
                     nR->bf = EH;
                     break;
                }
                case RH:
                {
                     (*p)->bf = EH;
                    nR->bf = LH;
                    break;
                 }
             }
             nRchd->bf = EH;
             rotateL(&((*p)->lchd));
             rotateR(p);
         }
     }
 }
 void BlanceRight(pBinTree *p)//从最小非平衡树开始调整
{
     pBinTree nR,nRchd;
    nR = (*p)->rchd; 

     switch (nR->bf){
    case RH:    //新插入的结点在左子树
        {
            (*p)->bf = EH;
             nR->bf = EH;
             rotateL(p);
             break;
         }
     case LH:    //新插入的结点在右子树
         {
            nRchd = nR->lchd;
             switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子？
             {
             case LH://
                 {
                    (*p)->bf = EH;
                     nR->bf = RH;
                     break;
                 }
             case EH://
                 {
                     (*p)->bf = EH;
                     nR->bf = EH;
                     break;
                 }
             case RH:
                 {
                     (*p)->bf = LH;
                     nR->bf = EH;
                     break;
               }
            }
            nRchd->bf = EH;
             rotateR(&((*p)->rchd));
            rotateL(p);
         }
     }
 }

然后再就是插入算法，这里采用递归的方式插入。

bool InsertAVL(pBinTree *T,int key,bool *taller)
 {
    if (!*T)
     {
         *T = (pBinTree)malloc(sizeof(BinTree));
         (*T)->data = key;
         (*T)->bf   = EH;
         (*T)->lchd = NULL;
         (*T)->rchd = NULL;
        *taller = true;
     }
     else

     {
         if (key  == (*T)->data)
         {
           *taller = false;
             return false;
         }
         if (key < (*T)->data)
        {
             if (!InsertAVL(&((*T)->lchd),key,taller))
             {
                 return false;
             }
             if (*taller)
            {
                 switch ((*T)->bf)
                 {
                 case LH:
                     {
                         BlanceLeft(T);
                         *taller = false;
                         break;
                     }
                 case EH:
                    {
                         (*T)->bf = LH;
                         *taller = true;
                         break;
                    }
                 case RH:
                     {
                         (*T)->bf = EH;
                         *taller = false;
                         break;
                      }
                  }
             }
         }
         else // key > (*T)->data
         {
             if (!InsertAVL(&((*T)->rchd),key,taller))
             {
                 return false;
             }
             if (*taller)
             {
                 switch ((*T)->bf)
                 {
                 case LH:
                     {
                         (*T)->bf = EH;
                         *taller = false;
                         break;
                     }
                 case EH:
                     {
                         (*T)->bf = RH;
                         *taller = true;
                         break;
                     }
                 case RH:
                     {
                           BlanceRight(T);
                         *taller = false;
                         break;
                     }
                 } 

             }
         }
     }
     return true;
 }    

以上的代码用switch case 显得非常的繁琐。会导致删除结点的程序判断BF调整非平衡的步骤更多。

以后添加删除部分代码。

完整代码：

 // AVL.cpp : 定义控制台应用程序的入口点。
 //   

 #include "stdafx.h"

 #include
  #define LH  1
  #define EH  0
  #define RH -1

  typedef int dataType;   

  typedef struct BinTNode {
     dataType data;
     int bf;
     struct BinTNode *lchd,*rchd;
 }BinTree,*pBinTree;  

  void rotateL(pBinTree *p)
 {
     pBinTree r;
     r = (*p)->rchd; //r 为新的根

     (*p)->rchd = r->lchd;
     r->lchd = (*p);
     (*p) = r;
 }   

 void rotateR(pBinTree *p)
 {
     pBinTree r;
     r = (*p)->lchd; //r 为新的根

      (*p)->lchd = r->rchd; //新根节点的右孩子附到旧的根结点的左孩子
      r->rchd = (*p);
     (*p) = r;
 }  

  void BlanceLeft(pBinTree *p)//从最小非平衡树开始调整
  {
     pBinTree nR,nRchd;
     nR = (*p)->lchd;
     switch (nR->bf)
     {
         case LH:    //新插入的结点在左子树
          {
             (*p)->bf = EH;
             nR->bf = EH;
             rotateR(p);
             break;
         }
         case RH:    //新插入的结点在右子树
          {
             nRchd = nR->rchd;
             switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子？
              {
                 case LH://
                 {
                     (*p)->bf = RH;
                     nR->bf = EH;
                     break;
                 }
                 case EH://
                 {
                     (*p)->bf = EH;
                     nR->bf = EH;
                     break;
                 }
                 case RH:
                 {
                     (*p)->bf = EH;
                     nR->bf = LH;
                     break;
                 }
             }
             nRchd->bf = EH;
             rotateL(&((*p)->lchd));
             rotateR(p);
         }
     }
 }
 void BlanceRight(pBinTree *p)//从最小非平衡树开始调整
  {
     pBinTree nR,nRchd;
     nR = (*p)->rchd;  

     switch (nR->bf){
     case RH:    //新插入的结点在左子树

         {
             (*p)->bf = EH;
             nR->bf = EH;
             rotateL(p);
             break;
         }
     case LH:    //新插入的结点在右子树
          {
             nRchd = nR->lchd;
             switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子？
              {
             case LH://
                 {
                     (*p)->bf = EH;
                     nR->bf = RH;
                     break;
                 }
             case EH://
                 {
                     (*p)->bf = EH;
                     nR->bf = EH;
                     break;
                 }
             case RH:
                 {
                     (*p)->bf = LH;
                     nR->bf = EH;
                     break;
                 }
             }
             nRchd->bf = EH;
             rotateR(&((*p)->rchd));
             rotateL(p);
         }
     }
 } 

 bool InsertAVL(pBinTree *T,int key,bool *taller)
 {
     if (!*T)
     {
         *T = (pBinTree)malloc(sizeof(BinTree));
         (*T)->data = key;
         (*T)->bf   = EH;
         (*T)->lchd = NULL;
         (*T)->rchd = NULL;
         *taller = true;
     }
     else

     {
         if (key  == (*T)->data)
         {
             *taller = false;
             return false;
         }
         if (key < (*T)->data)
         {
             if (!InsertAVL(&((*T)->lchd),key,taller))
             {
                 return false;
             }
             if (*taller)
             {
                 switch ((*T)->bf)
                 {
                 case LH:
                     {
                         BlanceLeft(T);
                         *taller = false;
                         break;
                     }
                 case EH:
                     {
                         (*T)->bf = LH;
                         *taller = true;
                         break;
                     }
                 case RH:
                     {
                         (*T)->bf = EH;
                         *taller = false;
                         break;
                     }
                 } 

             }
         }
         else // key > (*T)->data
         {
             if (!InsertAVL(&((*T)->rchd),key,taller))
             {
                 return false;
             }
             if (*taller)
             {
                 switch ((*T)->bf)
                 {
                 case LH:
                     {
                         (*T)->bf = EH;
                         *taller = false;
                         break;
                     }
                 case EH:
                     {
                         (*T)->bf = RH;
                         *taller = true;
                         break;
                     }
                 case RH:
                     {
                           BlanceRight(T);
                         *taller = false;
                         break;
                     }
                 } 

             }
         }
     }
     return true;
 } 

 int _tmain(int argc, _TCHAR* argv[])
 {
     int a[] = {,,,,,,,,,};
     int i;
     bool taller;
     pBinTree T = NULL; 

     for (i=;i<;i++)
     {
         InsertAVL(&T,a[i],&taller);
     }
     getchar();
     return ;
 }