CSU 1963 Feed the rabbit（斜率优化dp）

http://acm.csu.edu.cn/csuoj/problemset/problem?pid=1963

题意：
有m个坑，每只兔子会在ti时刻回到坑中，现在有n个人，每个人都可以从任意时间（<0也可以）从第一个坑出发，速度为1，如果路过的坑中有兔子，就给它喂食物，每只兔子喂一次即可，计算所有兔子等待时间的最短之和。

思路：
对于第i只兔子，如果有个人在y时间正好经过喂了它，那么那个人出发的时间为y-x。现在现计算出每只兔子的y-x值，记为t【】，并排好序。sum【】表示前i只兔子的y-x值。

接下来就是动态转移了，d【i】【j】表示第i个人正好经过第j只兔子时的最小等待时间。

那么状态转移方程就是

d[i][j]=min(d[i][j],d[i-][k]+(j-k)*t[j]-(sum[j]-sum[k]))

解释一下这个方程的意思：d【i-1】【k】表示上一个人正好经过第k只兔子时的最小等待时间，那么j~k之间的兔子肯定是要轮到第i个人来喂了，因为第i个人的出发时间更晚一些，所以j~k这些兔子肯定是要等待的，等待的时间就是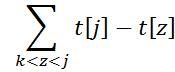，也就是上式的(j-k)*t[j]-(sum[j]-sum[k])。

理解了这个之后，接下来就是斜率优化dp的应用了，这样的状态转移方程也容易让人想到斜率优化dp。

设z<k<j，如果k的决策比z的决策更好，那么在上述的状态转移方程中满足

d[i-][k]+(j-k)*t[j]-(sum[j]-sum[k]) < d[i-][z]+(j-z)*t[j]-(sum[j]-sum[z])

整理得到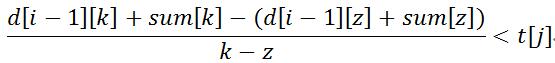，那这就是明显的斜率优化dp了。

所谓的斜率优化dp，就是每新插入一个点的时候，需要维护一条下凸的形状，对于会形成上凸的点，我们可以直接删去，因为它肯定不会是最优解。

那么如何维护呢？使用单调队列。

每次依次先检查队首的两个元素，如果满足上式，那么说明队首的第二个值更优，可以删除第一个值，直到第一个值比第二个元素更优。

然后是队尾的检查，如果新插入的点使得队尾的点成为了上凸点，那么就需要删去这个上凸点，直到没有上凸点产生。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn = 1e5+ ;

 int n, m, p;
 ll t[maxn];
 ll Q[maxn];
 ll sum[maxn];
 ll dis[maxn];
 ll d[][maxn];

 ll dy(int i, int j, int k)
 {
     return (d[i-][j]+sum[j])-(d[i-][k]+sum[k]);
 }

 ll dx(int j, int k)
 {
     return j-k;
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d%d",&n, &m, &p))
     {
         dis[]=;
         for(int i=;i<=n;i++)
         {
             scanf("%I64d",&dis[i]);
             dis[i]+=dis[i-];
         }

         for(int i=;i<=m;i++)
         {
             int x,y;
             scanf("%d%d",&x,&y);
             t[i]=y-dis[x];
         }

         sort(t+,t+m+);
         sum[]=;
         for(int i=;i<=m;i++)
             sum[i]=sum[i-]+t[i];

         for(int i=;i<m;i++)
             d[][i]=t[i]*i-sum[i];

         for(int i=;i<=p;i++)
         {
             int frt=, rear=-;
             for(int j=;j<=m;j++)
             {
                 while(frt<rear && dy(i,Q[frt+],Q[frt])<t[j]*dx(Q[frt+],Q[frt]))  frt++;
                 while(frt<rear && (dy(i,Q[rear],Q[rear-])*dx(j,Q[rear]))>=(dy(i,j,Q[rear])*dx(Q[rear],Q[rear-])))
                     rear--;
                 Q[++rear]=j;

                 int tmp=Q[frt];
                 d[i][j]=d[i-][tmp]-(tmp-j)*t[j]-(sum[j]-sum[tmp]);
             }
         }
         cout<<d[p][m]<<endl;
     }
     return ;
 }