poj1463 Strategic game【树形DP】

Strategic game

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 9582		Accepted: 4516

Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

For example for the tree: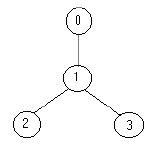 

the solution is one soldier ( at the node 1).

Input

The input contains several data sets in text format. Each data set represents a tree with the following description:

• the number of nodes
• the description of each node in the following format 
  node_identifier:(number_of_roads) node_identifier₁ node_identifier₂ ... node_identifier_{number_of_roads} 
  or 
  node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500);the number_of_roads in each line of input will no more than 10. Every edge appears only once in the input data.

Output

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following:

Sample Input

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

Sample Output

1
2

Source

Southeastern Europe 2000

题意：

给定一棵n个节点的树，如果在一个节点上放上一个士兵，所有与这个节点相连的边都可以被看守。现在希望所有的边都可以被看守，问需要最少放多少士兵。

思路：

比较典型的一个树形DP，我们用dp[i]表示以i为根的子树的最少士兵数。但是我们并不知道i上有没有士兵，转移方程就写不出来。

所以我们给dp再加一维，dp[i][1]表示以i为根并且i上有士兵的子树的最少士兵数，dp[i][0]为i上没有士兵。

那么对于某个节点rt，假设他的所有孩子的dp均已得到。

那么dp[rt][0] = dp[son][1]之和，因为他的每一个孩子都要有一个士兵。

dp[rt][1] = min(dp[son][0], dp[son][1])之和，即他的每一个孩子可以放士兵也可以不放士兵。

随便取一个节点作为树根，最后输出这个节点dp[rt][0]，dp[rt][1]的较小值即可。

 //#include <bits/stdc++.h>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<stdio.h>
 #include<cstring>
 #include<vector>
 #include<map>
 #include<set>

 #define inf 0x3f3f3f3f
 using namespace std;
 typedef long long LL;

 int n;
 const int maxn = ;
 vector<int>edge[maxn];
 int dp[maxn][];

 void dfsdp(int rt, int fa)
 {
     dp[rt][] = ;
     dp[rt][] = ;
     for(int i = ; i < edge[rt].size(); i++){
         int son = edge[rt][i];
         if(son == fa)continue;
         else dfsdp(son, rt);
         dp[rt][] += dp[son][];
         dp[rt][] += min(dp[son][], dp[son][]);
     }

 }

 int main(){

     while(scanf("%d", &n) != EOF){
         for(int i = ; i <= n; i++){
             edge[i].clear();
         }
         for(int i = ; i <= n; i++){
             int u, num;
             scanf("%d:(%d)", &u, &num);
             for(int j = ; j <= num; j++){
                 int v;
                 scanf(" %d", &v);
                 edge[u + ].push_back(v + );
                 edge[v + ].push_back(u + );
             }
         }

         dfsdp(, );
         printf("%d\n", min(dp[][], dp[][]));
     }
     return ;
 }