汉诺塔的python 动画演示
1.简介
古代有一座汉诺塔,塔内有3个座A、B、C,A座上有n个盘子,盘子大小不等,大的在下,小的在上,如图所示。有一个和尚想把这n个盘子从A座移到C座,但每次只能移动一个盘子,并且自移动过程中,3个座上的盘子始终保持大盘在下,小盘在上。在移动过程中可以利用B座来放盘子。
2.解决方法
解法的基本思想是递归。假设有 A、B、C 三个塔,A 塔有 


如此递归地使用下去, 就可以求解。
3.实现方法
python非动画实现:
def hanoi(n, a, b, c):
if n == 1:
print(a, '-->', c)
else:
hanoi(n - 1, a, c, b)
hanoi(1 , a, b, c)
hanoi(n - 1, b, a, c)
# 调用
n = input("")
hanoi(n, 'A', 'B', 'C')
python动画实现:
代码引用https://blog.csdn.net/BeerBread134/article/details/69226991
代码最多能运行7阶汉诺塔,不过稍微改一下整体参数还是可以做到“任意”阶数的。主要用了递归和栈的想法,用turtle实现。
import turtle class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - 1]
def size(self):
return len(self.items) def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize(10)
t.speed(100)
t.goto(400*(k-1), 100)
t.down()
t.goto(400*(k-1), -100)
t.goto(400*(k-1)-20, -100)
t.goto(400*(k-1)+20, -100)
drawpole_1(0)#画出汉诺塔的poles[0]
drawpole_1(1)#画出汉诺塔的poles[1]
drawpole_1(2)#画出汉诺塔的poles[2] def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(1,8-i)
plates[i].goto(-400,-90+20*i)
plates[i].showturtle()
return plates def pole_stack():#制造poles的栈
poles=[Stack() for i in range(3)]
return poles def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-1)*400,150)
plates[mov].goto((tp-1)*400,150)
l=poles[tp].size()#确定移动到底部的高度(恰好放在原来最上面的盘子上面)
plates[mov].goto((tp-1)*400,-90+20*l) def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= 1:
moveTower(plates,poles,height-1,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-1,withPole,toPole,fromPole) myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()
运行结果:
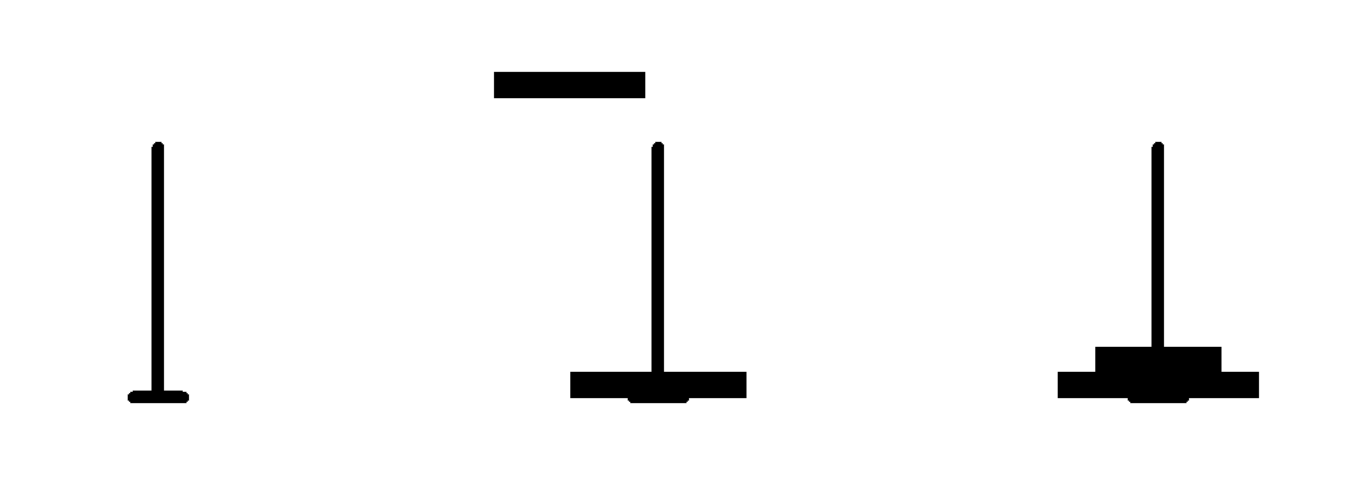
汉诺塔的python 动画演示的更多相关文章
- 经典问题(c++/python)素数、杨辉三角(金字塔型)、统计单词数、简单计算器、密码安全程度、凯撒密码加密、汉诺塔 (python课设实验实例)-- biaobiao88
[编写程序,输人一个大于2的自然数,然后输出小于该数字的所有素数组成的列表.]所谓素数,是指除了1和自身之外没有其他因数的自然数,最小的素数是2,后面依次是3.5.7.11.13... c++代码: ...
- 汉诺塔问题python
count = 0def hanoi(n,src,mid,dst): global count if n == 1: print("{}:{}->{}".format(1,s ...
- Python实现汉诺塔问题的可视化(以动画的形式展示移动过程)
学习Python已经有一段时间了,也学习了递归的方法,而能够实践该方法的当然就是汉诺塔问题了,但是这次我们不只是要完成对汉诺塔过程的计算,还要通过turtle库来体现汉诺塔中每一层移动的过程. 一.设 ...
- Python实现:汉诺塔问题
汉诺塔问题不管在任何编程语言里都是经典问题,是采用递归算法的经典案例,该问题可以抽象如下: 一 .3根圆柱A,B,C,其中A上面串了n个圆盘 二 .这些圆盘从上到下是按从小到大顺序排列的,大的圆盘任何 ...
- Python之汉诺塔递归运算
汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆 ...
- javascript实现汉诺塔动画效果
javascript实现汉诺塔动画效果 当初以为不用html5也很简单,踩了javascript单线程的大坑后终于做出来了,没事可以研究下,对理解javascript的执行过程还是很有帮助的,代码很烂 ...
- 1.python算法之汉诺塔
代码如下: #!/usr/bin/env python # encoding: utf-8 """ @author: 侠之大者kamil @file: 汉诺塔.py @t ...
- python解决汉诺塔问题
今天刚刚在博客园安家,不知道写点什么,前两天刚刚学习完python 所以就用python写了一下汉诺塔算法,感觉还行拿出来分享一下 首先看一下描述: from :http://baike.baidu. ...
- 汉诺塔 python版
汉诺塔问题:如果将n个盘子(由小到大)从a通过b,搬到c,搬运过程中不能出现小盘子在大盘子下面的情况. 思路分析:假设前要移动第100个盘子,分两步走,移动第99个:再移动第100个:而要移动第99个 ...
随机推荐
- Spring JMX之三:通知的处理及监听
通过查询MBean获得信息只是查看应用状态的一种方法.但当应用发生重要事件时,如果希望 能够及时告知我们,这通常不是最有效的方法. 例如,假设Spittr应用保存了已发布的Spittle数量,而我们希 ...
- iOS界面设计,12个优秀案例激发你的灵感
总所周知,iOS和Android是当今两大移动平台,前者采用Human Interface Design,后者采用Material Design.作为设计师,尤其是App设计师,总是会在这两者进行设计 ...
- 441. Arranging Coins
static int wing=[]() { std::ios::sync_with_stdio(false); cin.tie(NULL); ; }(); class Solution { publ ...
- RECONSUME_LATER
Failure consumption,later try to consume. ================MessageExt [queueId=0, storeSize=134, queu ...
- 排序:快速排序Quick Sort
原理,通过一趟扫描将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序 ...
- 封装MongoDB的 asp.net 链接类
using System;using System.Collections.Generic;using System.Linq;using MongoDB; /// <summary>// ...
- MYC编译器源码分析之程序入口
前文.NET框架源码解读之MYC编译器讲了MyC编译器的架构,整个编译器是用C#语言写的,上图列出了MyC编译器编译一个C源文件的过程,编译主路径如下: 首先是入口Main函数用来解析命令行参数,读取 ...
- Java Socket实现基于TCP和UDP多线程通信
一.通过Socket实现TCP编程 1.1 TCP编程 TCP协议是面向连接,可靠的,有序的,以字节流的方式发送数据.基于TCP协议实现网络通信的类有客户端的Socket类和服务器端的ServerSo ...
- [Elixir005] 查看指定数据的详细信息 i helper
elixir在1.2后增加了一个新的特性i helper. 在iex shell中使用i可以查看任意数据的数据类型和详细描述 #查看变量描述 iex(1)> i {:test, "Th ...
- Hadoop各个组件与端口
组件 Daemon 端口 配置 说明 HDFS DataNode 50010 dfs.datanode.address datanode服务端口,用于数据传输 HDFS DataNode 50075 ...
