【bzoj1502】[NOI2005]月下柠檬树 自适应Simpson积分

题目描述

李哲非常非常喜欢柠檬树，特别是在静静的夜晚，当天空中有一弯明月温柔地照亮地面上的景物时，他必会悠闲地坐在他亲手植下的那棵柠檬树旁，独自思索着人生的哲理。李哲是一个喜爱思考的孩子，当他看到在月光的照射下柠檬树投在地面上的影子是如此的清晰，马上想到了一个问题：树影的面积是多大呢？李哲知道，直接测量面积是很难的，他想用几何的方法算，因为他对这棵柠檬树的形状了解得非常清楚，而且想好了简化的方法。李哲将整棵柠檬树分成了n 层，由下向上依次将层编号为1,2,…,n。从第1到n-1 层，每层都是一个圆台型，第n 层(最上面一层)是圆锥型。对于圆台型，其上下底面都是水平的圆。对于相邻的两个圆台，上层的下底面和下层的上底面重合。第n 层(最上面一层)圆锥的底面就是第n-1 层圆台的上底面。所有的底面的圆心(包括树顶)处在同一条与地面垂直的直线上。李哲知道每一层的高度为h1,h2,…,hn，第1 层圆台的下底面距地面的高度为h0，以及每层的下底面的圆的半径r1,r2,…,rn。李哲用熟知的方法测出了月亮的光线与地面的夹角为alpha。

 

为了便于计算，假设月亮的光线是平行光，且地面是水平的，在计算时忽略树干所产生的影子。

李哲当然会算了，但是他希望你也来练练手

输入

第1行包含一个整数n和一个实数alpha，表示柠檬树的层数和月亮的光线与地面夹角(单位为弧度)。

第2行包含n+1个实数h0,h1,h2,…,hn，表示树离地的高度和每层的高度。

第3行包含n个实数r1,r2,…,rn，表示柠檬树每层下底面的圆的半径。

上述输入文件中的数据，同一行相邻的两个数之间用一个空格分隔。

输入的所有实数的小数点后可能包含1至10位有效数字。

1≤n≤500，0.3<alpha<π/2，0<hi≤100，0<ri≤100

输出

输出1个实数，表示树影的面积。四舍五入保留两位小数。

样例输入

2 0.7853981633
10.0 10.00 10.00
4.00 5.00

样例输出

171.97

---

题解

自适应Simpson积分

根据数学知识：在平行光投影下，圆的半径保持不变，位置为 高度/tanα ；圆台/圆锥的侧面投影为两圆/一圆一点的外公切线。

那么先将圆的位置求出，然后依次求相邻两圆公切线并将线段记录，此时注意内切/内含的两个圆是没有外公切线的。这里求公切线使用了射影定理。

如下图：

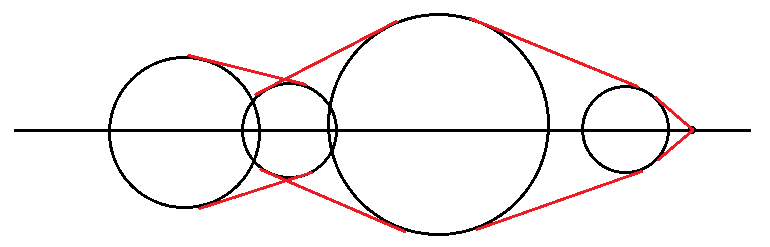
其中黑色的是投影后的圆，红色的是公切线段。

那么我们要求的就是最外层轮廓所围成的图形的面积。由于对称性因此只需要求出上半部分然后乘2。

注意到上半部分的外层轮廓形成了连续的一段函数，因此考虑使用自适应Simpson积分来求面积。

Simpson积分：对于三次及以下多项式函数，有 $\int_l^rf(x)dx=(r-l)·\frac {f(l)+f(r)+4f(\frac{l+r}2)}6$ 。
自适应Simpson积分：对于任意连续函数 $f(x)$ 求 $\int_l^rf(x)dx$，先将其当作三次函数使用Simpson积分求出 $[l,r]$ 、$[l,mid]$ 和 $[mid+r]$ 的面积，如果左半部分和右半部分面积之和与总面积之差满足精度要求则返回，否则递归左右并求和作为总面积。

本质上相当于插一个三次函数，如果差得比较多则递归左右。

回过头来看本题，问题变为：给出 $x$ ，求 $f(x)$ 。显然可以在每个圆和每条线段上（如果存在）求出 $x$ 的函数值，取最大值即为 $f(x)$ 。

注意精度要设得小一些，因为求和的部分使误差增大。

时间复杂度 $O(跑得过)$ 。

#include <cmath>
#include <cstdio>
#include <algorithm>
#define N 510
#define eps 1e-5
using namespace std;
struct circle
{
	double x , r;
}c[N];
struct line
{
	double x1 , y1 , x2 , y2;
}l[N];
double h[N];
int n , m;
inline double squ(double x)
{
	return x * x;
}
inline double f(double p)
{
	int i;
	double ans = 0;
	for(i = 1 ; i <= n ; i ++ )
		if(p >= c[i].x - c[i].r && p <= c[i].x + c[i].r)
			ans = max(ans , sqrt(squ(c[i].r) - squ(p - c[i].x)));
	for(i = 1 ; i <= m ; i ++ )
		if(p >= l[i].x1 && p <= l[i].x2)
			ans = max(ans , l[i].y1 + (p - l[i].x1) * (l[i].y2 - l[i].y1) / (l[i].x2 - l[i].x1));
	return ans;
}
inline double calc(double l , double r)
{
	return (r - l) * (f(l) + f(r) + f((l + r) / 2) * 4) / 6;
}
double simpson(double l , double r , double s)
{
	double mid = (l + r) / 2 , x = calc(l , mid) , y = calc(mid , r);
	if(fabs(x + y - s) <= eps) return s;
	return simpson(l , mid , x) + simpson(mid , r , y);
}
int main()
{
	int i;
	double alpha , t , L = 1e9 , R = -1e9;
	scanf("%d%lf" , &n , &alpha) , n ++ ;
	for(i = 1 ; i <= n ; i ++ ) scanf("%lf" , &h[i]) , h[i] += h[i - 1] , c[i].x = h[i] / tan(alpha);
	for(i = 1 ; i < n ; i ++ ) scanf("%lf" , &c[i].r);
	for(i = 1 ; i < n ; i ++ )
	{
		if(c[i + 1].x - c[i].x > fabs(c[i + 1].r - c[i].r))
		{
			m ++ ;
			t = c[i].r * (c[i].r - c[i + 1].r) / (c[i + 1].x - c[i].x) , l[m].x1 = c[i].x + t , l[m].y1 = sqrt(squ(c[i].r) - squ(t));
			t = c[i + 1].r * (c[i].r - c[i + 1].r) / (c[i + 1].x - c[i].x) , l[m].x2 = c[i + 1].x + t , l[m].y2 = sqrt(squ(c[i + 1].r) - squ(t));
		}
	}
	for(i = 1 ; i <= n + 1 ; i ++ ) L = min(L , c[i].x - c[i].r) , R = max(R , c[i].x + c[i].r);
	printf("%.2lf\n" , 2 * simpson(L , R , calc(L , R)));
	return 0;
}